1328

New method to characterize and correct with sub-µs precision gradient delays in bipolar multi-spoke RF pulses

Vincent Gras¹, Alexandre Vignaud¹, Alexis Amadon¹, Franck Mauconduit², Denis Le Bihan¹, and Nicolas Boulant¹

¹UNIRS, CEA/DRF/I2BM/Neurospin, Gif-sur-Yvette, France, ²Siemens Healthcare, Saint Denis, France

Synopsis

Small gradient delays with respect to radiofrequency (RF) pulses can have disastrous effects on the performance of bipolar spokes RF pulses employed in parallel transmission (pTx) to mitigate RF field inhomogeneity problems. This work reports a new method to characterize this delay with a precision of ~20 ns, shown to appear necessary for high performance pTx. By the same token, the same physics principles underlying the method suggest a way to correct for it by simply phase-shifting every second spoke RF pulse. The technique is validated with measurements on a water phantom and on an adult volunteer at 7T.

Purpose

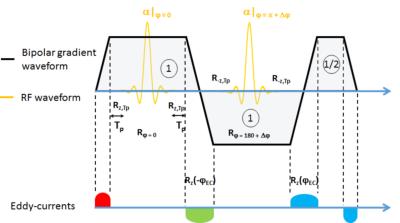
Multi-spokes RF pulses constitute a powerful approach in pTx to mitigate the RF inhomogeneity problem at ultra-high field in 2D. To date experimental demonstrations have made extensive use of unipolar configurations due to their larger robustness against eddy-currents and gradient delays^1,2,3 compared to bipolar implementations. Different MR methods to characterize this delay exist but may be SNR limited⁴ or may require additional equipment⁵. The method reported here relies on a simple $$$\alpha_{0^{\circ}}-\alpha_{180^{\circ}+\Delta\!\phi}$$$ bipolar 2-spoke experiment (Fig.1). In the absence of gradient delays and eddy-currents, this pulse sequence yields zero signal when $$$\Delta\!\phi=0$$$. As we shall demonstrate, gradient delays however will yield an effective phase-shift of the second RF pulse proportional to the carrier frequency offset used to excite the slice of interest. By determining the $$$\Delta\!\phi$$$ value restoring a minimum of signal, the gradient delay thus can be deduced with good accuracy.

Method

The delay characterization measurement is depicted in Fig.1. The blips shown in the figure correspond to zero-order eddy-currents ($$$\Delta\!B_0(t)$$$ envelopes) inherent to the presence of slice selection gradient ramps and which need to be modelled for an accurate analysis. With spoiled GRE sequences, the first (red blip in Fig.1) and last (blue blip) eddy-currents, the refocusing gradient lobe, the first rising gradient slope before the first RF pulse and the descending gradient slope after the second pulse do not affect the flip angle and thus shall be ignored. During the first gradient lobe and with a gradient delay $$$\Delta\!t$$$, the gradient during $$$T_p-\Delta\!t$$$ induces a rotation $$$R_{z,T_p-\Delta\!t}$$$ on the spins around $$$z$$$ with an angle of rotation proportional to $$$T_p-\Delta\!t$$$. The RF pulse during the first plateau generates the rotation $$$R_{\phi=0}$$$ where, importantly, $$$\phi$$$ corresponds to the global phase of the RF pulse and not the axis of rotation (which may be pointing between the $$$z$$$-axis and the transverse plane). The second pulse, except for the phase change, should be the time-reversed of the first. The rotation induced by the second pulse thus is $$$R_{\phi=\pi+\Delta\!\phi}$$$. The residual eddy-current between the two RF sub-pulses (green envelope in Fig.2) generates $$$R_z(-\phi_{\text{EC}})$$$, i.e. a rotation of angle $$$-\phi_{\text{EC}}$$$ around $$$z$$$. In the absence of a static $$$\Delta\!B_0$$$ offset, the rotation matrix can be shown to be equal to:

$$R_{\text{TOT}} = R_{-z,T_p-\Delta\!t}R_{\phi=\pi+\Delta\!\phi+\phi_{\text{EC}}-2\delta}R_{\phi=0}R_{z,T_p-\Delta\!t},$$

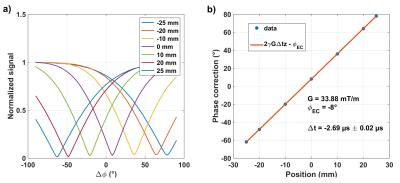
where $$$\delta=\gamma{G_z}\Delta_t$$$, $$$G$$$ being the gradient amplitude and $$$z$$$ the slice position. The eddy-current and gradient delay thus effectively induce a phase-shift on the second RF pulse. If $$$\Delta\!\phi=2\delta-\phi_{\text{EC}}$$$, then the rotation matrix above becomes Identity and there should be no signal. Thus by determining at different slice locations the $$$\Delta\!\phi$$$ value which returns a minimum of signal, the delay $$$\Delta\!t$$$ can be recovered by linear regression of $$$\Delta\!\phi$$$ versus $$$z$$$. Axial measurements were performed at 7T at -25,-20,-10,0,10,20 and 25 mm from the isocenter on a water phantom and $$$\Delta\!\phi$$$ was swept across the interval $$$[-90^{\circ};90^{\circ}]$$$. Once the delay and zero order eddy-current terms $$$\Delta\!t$$$ and $$$\phi_{\text{EC}}$$$ were recovered, their prospective correction was implemented in tailored bipolar 2-spoke configurations² on the same phantom and in vivo with multi-slice T₂*-weighted GRE protocols (25 slices, TE=15 ms, TR=936 ms, FA=30°, 0.5×0.5×2 mm³ voxels), by phase-shifting the second sub-pulse according to the slice locations. The results were compared to the unipolar 2-spoke implementations as a reference.

Results

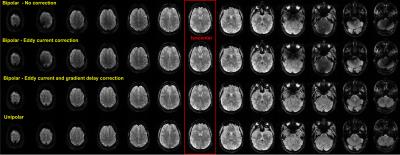
Figure 2 reports the phase sweep experiment on the phantom. Linear regression on the second sub-plot returned $$$\phi_{\text{EC}}=-8^{\circ}$$$ and $$$\Delta\!t=-2.69\pm0.02$$$ µs. This delay, if not corrected, can induce an effective phase shift of the second sub-pulse as large as 198° for $$$G=$$$40 mT/m and $$$z=$$$6 cm, which explains why this effect can quickly become disastrous for multi-spoke pulse performance. Fig.3 (phantom) and Fig.4 (in vivo) illustrate this behavior with signal voids appearing away from the isocenter. In this setup, after correction of the gradient delay and eddy-current by phase-shifting the second pulse, the results of the bipolar configuration became very similar to the ones obtained with the unipolar configuration.

Discussion and conclusion

The effective phase-shift induced by a gradient delay being proportional to the carrier frequency offset, an accuracy better than 0.1 µs is desired for high performance bipolar spokes implementations, a performance hardly obtainable with time-shifting methods constrained by RF raster times typically ≥ 1 µs. Because the phase of RF pulses is well-controlled in modern MR equipment, with ~20 ns precision, the method reported here is simple and appears to meet this demand. By the same token, it yields as a bonus the zero-order eddy-current phase correction that should be applied for optimal results.

Acknowledgements

The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2013-2018), ERC Grant Agreement n. 309674.

References

[1] Sharma et al. MRM 2016 ;74 :747-755. [2] Gras et al. MRM; doi 10.1002/mrm.26491. [3] Tse et al. ISMRM 23rd 2015; p. 0546. [4] Davies et al. MRM 2005;53:231-236. [5] Brunner et al. NMR in biomed 2016;29:1162-1172.

Figures

Bipolar 2-spoke configuration used for gradient delay and zero order eddy-current characterization. The RF sub-pulses are padded with zeros before and after (duration T_p). Rotations around the z axis are induced during these periods which are affected by a gradient delay Δt (R_z,Tp±Δt and R_-z,Tp±Δt, the sign of the rotation depending on the sign of the gradient). The RF pulses combined with the gradient fields generate rotations denoted as R_φ=0 and R_φ=π+Δφ respectively (global phase of the RF field in subscript). The middle eddy-currents engender rotations around z, R_z(φ_EC).

Gradient delay and zero order eddy-current measurements results. Subplot a) reports the normalized signal as a function of Δφ in a region of interest where ΔB₀~0 and at several slice (z) locations. For each location, the minimum is achieved when the action of the bipolar 2-spoke pulse is null at the center of the slice, i.e. when the correct phase correction is applied. In b), the value of Δφ where the minimum occurs is plotted versus z, returning after linear regression Δt=-2.69±0.02 µs and φ_EC=-8°.

Results of the phantom experiments (13 out of the 25 axial slices shown, 1 cm separates the shown adjacent slices). From top to bottom: bipolar 2-spoke pulses with no correction, bipolar 2-spoke pulses with eddy-current correction only, bipolar 2-spoke pulses with eddy-current and gradient delay compensation, unipolar 2-spoke pulses. The RF spoke-pulses for the bipolar case were tailored for each slice individually to achieve a target flip angle of 30°. The same RF coefficients and optimized k-space trajectory were applied to the unipolar case. The unipolar and corrected bipolar spoke-pulses returned nearly identical results.

In vivo T₂*-weighted axial images acquired at 7T (13 out of the 25 axial slices shown, 1 cm separates the shown adjacent slices). The same observations as for the phantom results can be made with very heterogeneous excitation profiles and signal voids away from isocenter when the gradient delay is not corrected.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1328