Synopsis

Fast spin echo acquisition plays an essential role in a worthy of MRI applications. But the flip angles of refocus pulses are conventionally designed intuitively. In this work, we proposed a global scheme that can provide a comprehensive framework for flip angled design and proposed the requirement with a well-proposed optimization problem. The performance of the proposed method was demonstrated on the correction of T2 blurring with numerical simulation.

Purpose

Fast spin echo (FSE) acquisition has been used widely in MRI applications. It provides high imaging speed and SNR. Aggressively long echo trains can lead to unacceptable blurring, however. Reduced refocusing flip angles are widely used to moderate this blurring. Flip angles schemes were proposed to reach maximum at the last echo [1] or attempt to maintain constant signal until the kspace center was covered and then increase flip angles linearly [2][3]. The design of reduced flip angle trains, however, is generally performed using heuristic rather than systematic methods. The target function was not well-described in these designs and it can result in suboptimal flip angles and reduced SNR.

The goal of this study is to provide optimal SNR with combined design of flip angle and echo scaling correction. A framework of variable flip angle design was proposed, which provides a globally optimized solution to control blurring and optionally to control SAR or other limitations.

Method

The proposed method has three major distinguishing features.

First, we allow for achieving a targeted signal response by a combination of flip angle and multiplicative scaling corrections. This allows maximal flexibility.

Second, the target of this design is expressed analytically. For example in T2 blurring correction, suppose the acquired FSE signal S is corrected by scaling to match a target window W (e.g. Hann window). The SNR of the resulting image can be expressed as:

$$SNR=\frac{M_0}{S}\frac{\sum W}{\sqrt{\sum{(\frac{W}{S}})^2}}$$

where M0 is the baseline signal, $$$\sigma$$$ is the noise level and. Since the SNR only depends on the signal S, the optimal solution can be provided by minimizing the cost function:

$$\sum{(\frac{W}{S}})^2$$

Besides SNR, the SAR of variable flip angles can also be imposed with an additional constraint on the sum of square of the flip angles $$$\theta$$$ :

$$\sum{\theta^2}$$

The third feature of the proposed method is global optimization of flip angle echo scaling design. Conventionally, flip angles were designed sequentially, because the FSE signal depends on the history of flip angles. This design, however, may limit the performance of later flip angles and result in suboptimal result. In the proposed method, all flip angles, and the corresponding multiplicative scale factors, were designed together with a global optimization algorithm [4].

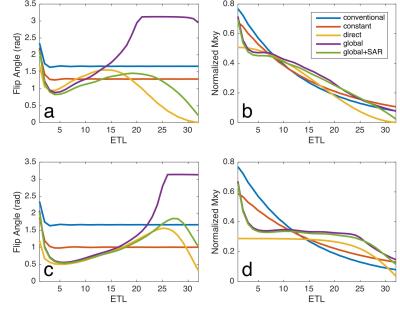
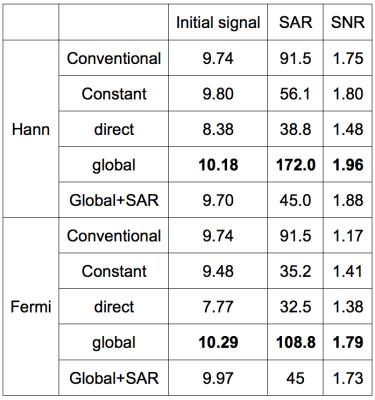
Here, we used a centric ordered 3D Stack of Spirals sequence as an example. The flip angle design will reduce the blurring and provide optimal SNR in correction. 32 slices were acquired in the same echo train and a single tissue component with T1 1.6s and T2 0.1s was imaged. The echo spacing was 10ms. The Extended phase graph algorithm [5] was implemented in a custom MATLAB program. Five flip angles schemes were designed: (1) the conventional design with asymptotic constant amplitude [6], (2) asymptotic constant amplitude optimized for correction, (3) direct target window response, (4) the proposed global design and (5) the global method with SAR limited to 50% of scheme (1). Both Hann and Fermi windows were used in the design and scalar correction. The performance of each scheme was quantified by initial signal level ($$$\sum S$$$), SAR and SNR of the corrected image.

Result and Discussion

The variable flip angle designs and resulting signals are shown in Figure 1. The proposed global optimized design tended to have smaller flip angles at the beginning of the echo train and increased the flip angles to maintain the echo amplitude in the later echoes. However, the flip angle approached pi at the last few echoes. In contrast, the global design with 50% SAR limitation resulted in largely reduced flip angle, while maintaining a similar signal response.

The result is more clearly shown in Table 1. The proposed global design provided the highest initial signal and the highest SNR in the corrected images, at the expense of SAR. With the SAR limitation, although the performance of the proposed method was slightly reduced, it resulted in superior SNR and safer SAR, comparing with conventional, asymptotic constant amplitude and direct target window design.

Conclusion

Acknowledgements

References

[1] X. Liang, A. Connelly, J. D. Tournier, and F. Calamante, “A variable flip angle-based method for reducing blurring in 3D GRASE ASL,” Phys Med Biol, vol. 59, no. 18, pp. 5559–5573, 2014.

[2] V. G. Kemper, F. De Martino, E. Yacoub, and R. Goebel, “Variable flip angle 3D-GRASE for high resolution fMRI at 7 tesla,” Magn. Reson. Med., vol. 76, no. 3, pp. 897–904, 2016.

[3] R. F. Busse, H. Hariharan, A. Vu, and J. H. Brittain, “Fast spin echo sequences with very long echo trains: Design of variable refocusing flip angle schedules and generation of clinical T2 contrast,” Magn. Reson. Med., vol. 55, no. 5, pp. 1030–1037, 2006.

[4] Z. Ugray, L. Lasdon, J. Plummer, F. Glover, J. Kelly, and R. Martí, “Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization,” INFORMS J. Comput., vol. 19, no. 3, pp. 328–340, Aug. 2007.

[5] M. Weigel, “Extended phase graphs: Dephasing, RF pulses, and echoes - Pure and simple,” J. Magn. Reson. Imaging, vol. 41, no. 2, pp. 266–295, 2015.

[6] D. C. Alsop, “The sensitivity of low flip angle RARE imaging,” Magn. Reson. Med., vol. 37, no. 2, pp. 176–184, 1997.