Synopsis

A computationally-efficient constrained minimum-time VERSE algorithm is presented which is sufficiently fast that it could be used for real time VERSE’ing of RF pulses during pulse sequence prescription.

Purpose

Variable-rate selective excitation (VERSE¹) is a technique that allows one to modify an RF and gradient pulse pair in concert, in order to reduce peak B1, reduce SAR, or reduce the pulse time. In 2004 Hargreaves et al.² discussed the basics of an iterative minimum-time VERSE algorithm - with Matlab compatible mex code available online³. The work presented here follows a similar approach but with a novel implementation. Note that there is a method for minimum-time VERSE’ing multi-dimensional pulses, based on optimal control theory concepts^4,5. This is a direct method involving the solution of a differential equation; and is not further discussed here.

Often, VERSE pulses are created off-line, and then used pre-formed by the pulse sequence, with perhaps nothing more than a gradient scaling to change the slice thickness. This approach is often satisfactory, but does not always make the optimal use of gradient and RF hardware. For instance, this approach typically designs for worst case peak RF amplitude (heaviest patients) and a maximum gradient strength to support the minimum slice thickness. Further, this patient and sequence prescription related optimization is becoming more critical with the introduction of simultaneous multislice (SMS) imaging (see for example Barth et al.⁶) where VERSE is a critical component of peak B1 and SAR reduction strategies.

Methods

We start by designing a piece-wise constant slice-selective RF pulse with a constant gradient, constant time intervals, and desired profile using, for instance, the SLR algorithm⁷. This gives a discrete series of $$$b_{i}$$$ values representing the RF pulse, where $$$i$$$ denotes an integer position within the series. The associated initially constant gradient segment amplitudes and time interval values are represented by $$$(g_{i} = g_{s}, d_{i} = d_{s})$$$, respectively.

The maximum RF, gradient and slewrate strengths are denoted by $$$B_{max}, G_{max}, SR_{max}$$$, respectively.

The first step is a time independent compression of the time intervals to utilize the maximum gradient.

$$d_{i} \Leftarrow d_{i} * g_{s} / G_{max}$$

From now on we just perform time dilations. The second step is to dilate the time intervals such that the RF strength constraint is met.

$$d_{i} \Leftarrow d_{i} * max(1, |b_{i}| / B_{max})$$

From the VERSE condition¹ we have that $$$d_{i} g_{i} = d_{s} g_{s}$$$. Therefore a finite difference approximation to the slewrate is given by

$$sr_{i} = d_{s} g_{s} \frac{2(d_{i+1}-d_{i})}{d_{i+1}d_{i}(d_{i+1}+d_{i})}$$

For conciseness define $$$SR_{n} = SR_{max} / d_{s} g_{s}$$$; and $$$D_{i} = d_{i+1} - d_{i}$$$, $$$S_{i} = d_{i+1} + d_{i}$$$, and $$$P_{i} = d_{i+1}d_{i}$$$.

Now the strategy for meeting the slewrate constraint is: Wherever the slewrate constraint is violated, dilate (increase) the shorter of the two intervals by $$$e_{i}$$$ in order to meet the constraint. If the short interval is $$$d_{i}$$$, then, using the slewrate equation above, we have the requirement that

$$2(|D_{i}|-e_{i})=SR_{n}d_{i+1}(S_{i}d_{i}+e_{i}(S_{i}+d_{i})+e_{i}^{2})$$

It turns out that the quadratic dilation term can be ignored, and so we can easily solve for $$$e_{i}$$$, giving

$$d_{i}\Leftarrow d_{i}+e_{i} = d_{i} + \frac{(2|D_{i}|-SR_{n}S_{i}P_{i})}{(2+SR_{n}(d_{i+1}S_{i}+P_{i}))}$$

If $$$d_{i+1}$$$ is the shorter interval, then $$$d_{i}$$$ and $$$d_{i+1}$$$ are exchanged.

Typically this update will cause slewrate constraint violations at neighboring positions, and so this process it repeated a number of times.

Finally, the initial RF and gradient values are updated by

$$b_{i} \Leftarrow b_{i} * d_{s} / d_{i}$$

and

$$g_{i} \Leftarrow g_{i} * d_{s} / d_{i}$$

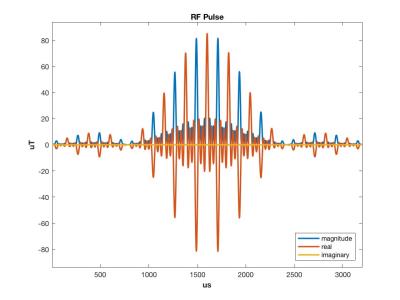
To demonstrate the convergence and the processing time of a Matlab implementation, the algorithm is applied to the reasonably complex 6-slice SMS pulse shown in figure 1. For the minimum-time VERSE calculation the maximum RF, gradient and slewrate values were 12uT, 30mT/m and 120T/m/s respectively. The time resolution of the initial waveforms was 2us.

Results

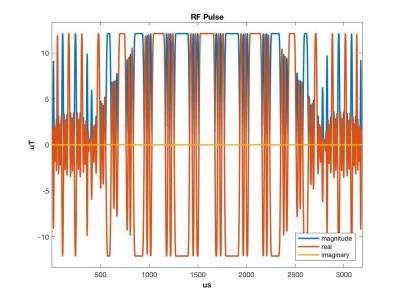
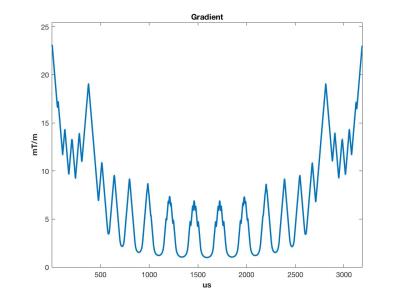
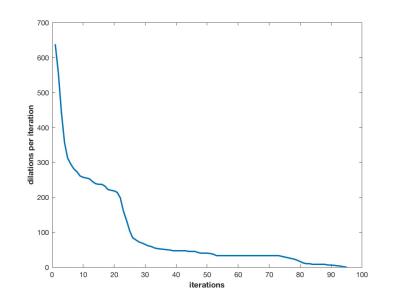
The resulting VERSE'd RF and gradient waveforms are shown in figures 2 and 3 respectively. The processing time was 6ms, requiring 95 iterations and 9206 individual dilations during the slewrate optimization. The number of dilations versus iteration number is shown in figure 4.

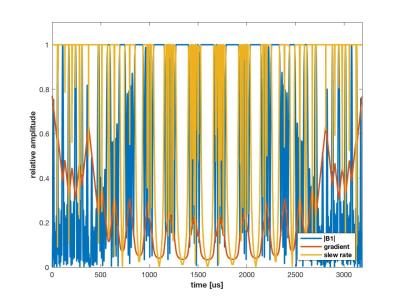
That the result is optimal is demonstrated in figure 5, which plots the normalized RF, gradient and slewrate values - at any time point at least one of these values should be 1. Note that in this case the maximum gradient value was not reached.

Discussion and Conclusion

We have presented a minimum-time VERSE algorithm which seems very efficient and optimal, and suitable for real-time use during pulse sequence prescription.

While difficult to formally prove the convergence of the algorithm, in our experience, with practical pulses, it always converged after at most a few hundred iterations.

Acknowledgements

References

1. Conolly S, Nishimura D, Macovski A, Variable-rate selective excitation, J Magn Reson 1988; 78:440-458

2. Hargreaves BA, Cunningham CH, Nishimura DG, Conolly SM, Variable-rate selective excitation for rapid MRI sequences, Magn Reson Med 2004; 52:590-597

3. http://www-mrsrl.stanford.edu/~brian/mintverse/

4. Lee D, Lustig M, Grissom WA, Pauly JM, Time-optimal design for multidimensional and parallel transmit variable-rate selective excitation, Magn Reson Med 2009; 61:1471-1479.

5. Lustig M, Kim S-J, Pauly JM, A fast method for designing time-optimal gradient waveforms for arbitrary k-space trajectories, IEEE Trans Med Imaging 2008; 27:866-873

6. Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA, Simultaneous multislice (SMS) imaging techniques, Magn Reson Med 2016; 75:63-81.

7. Pauly J, Le Roux P, Nishimura D, Macovski A, Parameter relations for the Shinnar - Le Roux selective excitation pulse design algorithm, IEEE Trans Med Imaging 1991; 10:53-65