1299

Correcting diffusion data for off-resonace effects, movement-induced signal loss and intra-volume movement.
Jesper L. R. Andersson1, Mark S. Graham2, Ivana Drobnjak2, Hui Zhang2, Nicola Filippini1, and Matteo Bastiani1

1Oxford University, Oxford, United Kingdom, 2University College London

Synopsis

An intra-volume movement model was added to an existing framework for correcting off-resonance distortions, movement-induced signal dropout and subject movement in diffusion data. It was validated on highly realistic simulated data with "normal" and "high" levels of subject movement. The results show that slice-wise movement parameters can be estimated with an accuracy of ~0.2mm and ~0.2degrees for translations and rotations respectively. The simulations also show that the method substantially decreases the difference in fidelity of FA between subjects who move a lot and subjects who move a little. We finally demonstrate how the method corrects telltale signs of intra-volume movement in real data.

INTRODUCTION

Subject movement is a serious problem when acquiring diffusion data. If not properly corrected it can cause spurious differences between cohorts with different propensities to move1. Methods to correct for intra-volume movement have been developed for fMRI2,3, but volume-to-volume methods4,5 dominate in practical use. Because of the long repetition time in diffusion imaging, compared to fMRI, there is a greater risk of significant movement during the acquisition of a volume. Here we present a method to correct intra-volume movement in diffusion data. It has been incorporated into a method for simultaneous correction of off-resonance distortions, movement-induced signal loss and subject movement6,7.

METHOD

One discrete cosine (DCT) set per volume was used to model each of the six rigid-body parameters as a piece-wise continuous function over time. Motion estimates was obtained by matching model-predictions of slices with observed slices. Estimates of movement, distortions and a list of outlier-slices was updated on each iteration.

The more difficult problem of reconstructing a corrected volume from a set of disparate slices was solved by a hybrid 2D+1D method. First all slices were spline-interpolated onto a regular 2D grid in the target space. This means that for each [x,y] coordinate pair in the target space there were a set of values irregularly sampled onto a 1D-column. For the cases where there were large gaps between successive points, they were complemented by model predictions. Finally, a cubic B-spline model was fitted to the irregular samples and interpolated values were calculated for the regular points in the z-direction. The strategy is explained graphically in figure 1.

VALIDATION

Realistic simulated diffusion data was created with a combination of eddy current-induced distortions, signal dropout and subject movement8. Data was generated for different amounts of subject movement, corresponding to "normal" and "large" movement and for "normal" SNR (20) and "good" SNR (40). It consisted of 32 volumes of b=700, 64 volume of b=2000 and 12 interspersed b=0 volumes. These data were corrected using our framework, either with the volume-to-volume model or with the slice-to-volume model.

Registration error was assessed by comparing the estimated and known error for each slice and defining the error as the square root of the mean squared difference.

Fractional anisotropy (FA) was calculated after motion correction with the volume-to-volume or the slice-to-volume model. This was done for "normal" and "large" movement and for both SNR levels.

The correction method was also tested on elderly subjects acquired as part of the Whitehall Project9. The subjects that were flagged as "potentially problematic" by the QC were inspected manually and the eight worst subjects were selected for testing the slice-to-volume correction on.

RESULTS

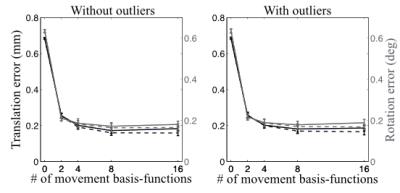
Figure 2 shows that the registration error, as assessed from simulated data, was substantially reduced. For these simulations it reached a plateau for four DCT-basis functions per volume and parameter. That may be partially because of the relatively smooth (in time) that was injected into the simulations. Importantly, the error remains approximately constant for up to 16 DCT-basis functions per volume and parameter, which means that it is feasible to use a high temporal resolution.

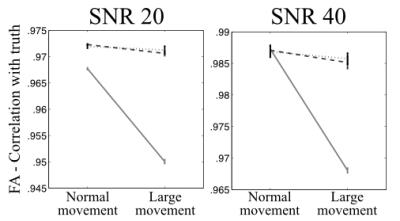
The fidelity of the estimated FA is shown in figure 3 for "normal" and "large" movement after correction with the volume-to-volume or slice-to-volume model. It can be seen that when using the volume-to-volume model the accuracy of FA values for data with "large" movement is much worse than for data with "normal" movement. When instead using the slice-to-volume model that difference is substantially (and significantly) smaller.

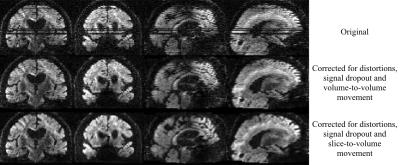
All data from the problematic Whitehall subjects looked much better after slice-to-volume correction. An example of a volume before and after correction is shown in figure 4. The volume originally shows severe movement-induced signal dropout and telltale signs of intra-volume movement (zig-zag edges). After correction for distortions, dropout and slice-to-volume movement it looks much better.

DISCUSSION

We have developed and validated a method to correct for intra-volume subject movement. Our results indicate that there is never a disadvantage to use the slice-to-volume method. I.e. the fidelity of the estimated FA improves or remains unchanged even for "normal" movement.

In the case of large movement there is a substantial improvement both in terms of registration error and FA accuracy. Importantly, it reduces the difference in FA accuracy between data affected by "normal" and "large" movement. We hope that will help alleviate the problem of spurious differences between cohorts with different tendencies to move.

Data acquired in eight elderly subjects that moved a lot shows very substantial improvement, as assessed by visual inspection, after slice-to-volume correction.

Acknowledgements

The authors gratefully acknowledge helpful discussions with Stamatios Sotiropoulos and Mark Jenkinson. We are also grateful to Klaus Ebmeier for making the data from the Whitehall project available to us. JLRA was funded by the Wellcome-Trust Strategic Award 098369/Z/12/Z and MSG by EPSRC grant EP/L504889/1 and by the EPSRC Centre for Doctoral Training (EP/L016478/1).

References

1. Yendiki A, Koldewyn K, Kakunoori S, et al Spurious group differences due to head motion in a diffusion MRI study. NeuroImage 2014;88:79–90.

2. Kim B, Boes JL, Bland PH, et al. Motion correction in fMRI via registration of individual slices into an anatomical volume. Magnetic Resonance in Medicine 1999;41:964–972.

3. Yeo DTB, Fessler JA, & Kim B. Concurrent correction of geometric distortion and motion using the map-slice-to-volume method in echo-planar imaging. Magnetic Resonance Imaging 2008;26:703–714.

4. Friston KJ, Ashburner J, Frith, CD, et al. Spatial registration and normalization of images. Human Brain Mapping 1995;2:165–189.

5. Jenkinson M, Bannister P, Brady JM & Smith S. Improved Optimisation for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. NeuroImage;17:825-841.

6. Andersson JLR & Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage 2016;125:1063–1078.

7. Andersson JLR, Graham MS, Zsoldos E, & Sotiropoulos SN. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage 2016;141:556-572.

8. Graham MS, Drobnjak I & Zhang H. Realistic simulation of artefacts in diffusion MRI for validating post-processing correction techniques. NeuroImage 2016;125:1079–1094.

9. Filippini N, Zsoldos E, Haapakoski R, et al. Study protocol: The whitehall II imaging sub-study. BMC Psychiatry 2014;14:159.

Figures

Fig 1. The figure shows an example (on the left) of a sequential acquisition where the subject "looked up" between the acquisitions of the red and green slices (slices 16 and 17). On the right it can be seen how slices 15--18 have been slotted into the target volume. It is further shown how for one voxel in slice 18 the unknown coordinates x', y' and z* are calculated, the slices is 2D interpolated at [x' y' 18] and how this value is placed at the coordinate [x y z*] in the target volume.

Fig 2. This figure shows the slice-wise registration error for data simulated with an SNR of 20 (as defined in the b=0), large movement and with and without outliers. The x-axis shows the number of DCT basis functions per parameter and volume, with 0 corresponding to volume-to-volume registration. The grey lines show the rotations and the black lines the translations. The solid lines correspond to a temporal regularisation weighting of 1 and the dashed to a weighting of 10.

Fig 3. This figure shows the fidelity of estimated FA from a data set with "normal" movement and from a data set with "large" movement. The correlation (across intracerebral voxels) between true and estimated FA when using the volume-to-volume movement model is shown with a solid grey line. The results for the slice-to-volume with 8 and 16 DCT components per parameter are shown as a dashed and a dotted line respectively.

Fig 4. This figure shows two coronal and two sagittal slices from a single volume acquired in an elderly subject. The top row shows the original data. The second row shows the results of correcting for off-resonance distortions, signal dropout and volume-to-volume movement. The third row shows the same, but with a slice-to-volume movement model.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1299