1297

Evaluation of prospective and retrospective motion correction exploiting the slice-based acquisition of fMRI

Malte Hoffmann¹ and Stephen J Sawiak^1,2

¹Wolfson Brain Imaging Centre, Department of Clinical Neurosciences, University of Cambridge, Cambridge, United Kingdom, ²Behavioural and Clinical Neuroscience Institute, Department of Psychology, University of Cambridge, Cambridge, United Kingdom

Synopsis

Motion artefacts are damaging to fMRI studies, masking real effects or forcing data to be discarded. Standard processing pipelines include linear registration steps between frames, though some groups proposed prospectively exploiting the slice-based nature of acquisition. The improvement this offers is rarely quantified as no “baseline” is available. Here, we simulated MRI acquisitions with a general slice-based navigation method to quantify the accuracy of prospective correction over retrospective registration. Compared to retrospective linear and non-linear techniques, registration of individual slices most accurately matched trial motion trajectories with better image quality than linear methods.

Purpose

Motion is damaging to fMRI studies, masking real activation or forcing data to be discarded. While standard processing pipelines include a linear registration step between frames, some groups propose improvements by prospectively exploiting the slice-based nature of acquisition^1,2. Quantification of this is hampered by the lack of a suitable baseline for comparison. Here, we use motion trajectories obtained from patients within a full MRI simulation comparing slice-wise prospective motion correction (PMC) with a retrospective approach. As it includes spin history effects producing data that could not be obtained otherwise, this approach allows direct quantitative comparison of PMC with a general navigation scheme against uncorrected and retrospectively corrected data.

Methods

MRI simulation

We simulated fMRI acquisitions with a general slice-based navigation method. Two groups of datasets were generated (“PMC on” and “off”), both based on identical representative trajectories derived from patients undertaking fMRI in a visual stimulation study³. For each of five low, medium and high motion scenarios, we computed 100 frames of 2D GE EPI with interleaved slice ordering and specifications matching those of the study, using Bloch equation simulations⁴ with tissue-parameter maps from BrainWeb⁵.

Motion-correction strategies

Gradient and RF parameters for the (n+1)^th slice acquisition were adaptively updated based on motion measured at the beginning of the n^th slice. This could be done using any tracking method, e.g. wireless probes⁶ or an image-based navigator⁷. We retrospectively corrected the “PMC-off” data using: (1) linear registration with SPM12⁸, (2) non-linear registration with MCFLIRT/FNIRT⁹, and (3) rigid-body registration of individual slices¹⁰ by minimising the sum of squared differences to a “moving” slice in a reference image without motion.

Numerical comparison

Image quality was evaluated as the root-mean-square deviation (RMSD) between each volume and a reference image without motion. We calculated the “RMS deviation”¹¹ between transforms derived using each registration algorithm and the injected trajectories: slice-based transforms were compared to the slice-wise average of non-linear warps of brain voxels, and volumetric linear transforms.

Results

MRI simulation

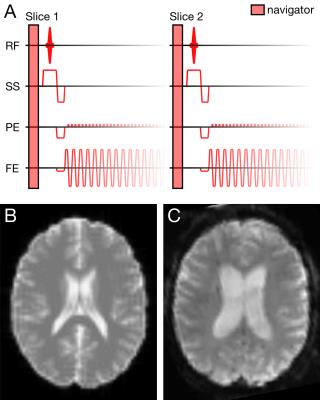
A simulated EPI slice is compared to a patient dataset acquired with identical sequence specifications in Figure 1. The motion (combined translations/rotations) detected in patient datasets was moderate (mean 1.4mm)³, though with some severe outliers. Here, the mean motion of low, medium and high motion trajectories was 0.06, 0.49 and 7.49mm, respectively.

Comparison of image quality

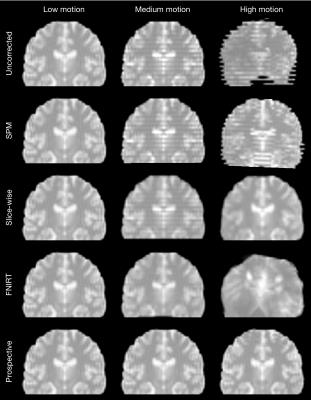
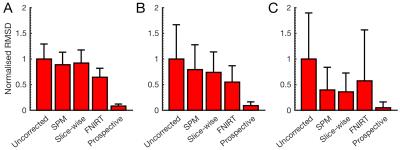
Figure 2 shows the difference between methods in typical images. There are no discernible differences at low motion. Slice-based registration mitigated the effect of medium through-plane motion, FNIRT removed it completely. FNIRT introduced unacceptable deformations at high in-plane motion, while slice-based registration restored the image at the expense of some blurring. Prospective correction performed best, removing all artefacts. Mean RMSD values across each motion category are compared in Figure 3.

Slice-based motion parameters

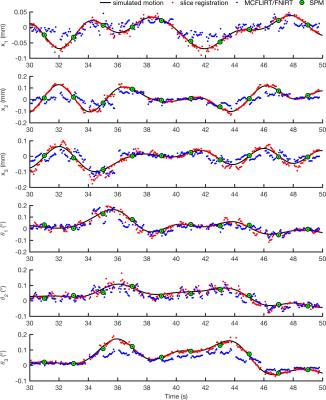
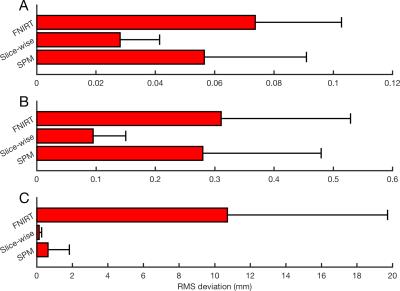
Figure 4 illustrates how typical linear, slice-based and non-linear transforms compare to the simulated motion. Marginal slices and those with less than 50% of the mean slice intensity were not registered. The mean RMS deviation between transforms estimated by each algorithm and the true motion is shown in Figure 5. Slice registration recovered the motion most closely.

Discussion

We quantified the performance for a direct comparison of prospective vs. retrospective correction in simulation, finding that prospective correction removed over 94% of errors introduced by motion, yielding image quality comparable to that of acquisitions without motion. Retrospective registration can partially compensate for motion. We showed that the performance of retrospective methods can be improved by exploiting the slice-wise nature of acquisition: although non-linear correction appeared to ameliorate datasets retrospectively, slice-based registration gave more realistic corrections.

The discrepancies in Figure 2 show that warps computed between frames with high levels of motion may be unreasonable, leading to spurious fMRI findings. Before sorting motion estimates chronologically, slice-wise averaged non-linear warps evolved more smoothly than shown in Figure 3: non-linear regularisation enforced a degree of smoothness between warps of neighbouring voxels, ill-suited for interleaved acquisitions. The incorporation of slice-based transforms into the regularisation of non-linear deformations may be useful in avoiding overfitting.

Conclusion

Prospective correction completely fixes the motion problem in fMRI, while retrospective correction partially compensates for motion. The performance of retrospective correction can be improved by exploiting the mechanism of slice-wise acquisition: compared to linear and non-linear techniques, registration of individual slices most accurately matched trial motion trajectories with better image quality than linear methods. Direct evidence of almost complete motion compensation with prospective correction could be of particular interest to resting-state fMRI users where motion can introduce spurious correlations.

Acknowledgements

The authors would like to thank the Cusanuswerk scholarship body (Bonn, Germany) for funding.

References

1. Speck O, Hennig J, Zaitsev M. Prospective real-time slice-by-slice motion correction for fMRI in freely moving subjects. MAGMA 2006;19(2):55-61.

2. Muraskin J, Ooi MB, Goldman RI, Krueger S, et al. Prospective active marker motion correction improves statistical power in BOLD fMRI. NeuroImage 2013;68:154-61.

3. Hoffmann M, Carpenter TA, Williams GB, and Sawiak SJ. A survey of patient motion in disorders of consciousness and optimization of its retrospective correction. Magn. Reson. Imaging 2015;33(3):346-350.

4. Hargreaves B. Bloch Equation Simulation. 2002. http://www-mrsrl.stanford.edu/~brian/bloch/. Accessed September 29, 2016.

5. Collins DL, Zijdenbos AP, Kollokian V, et al. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging 1998;17(3):463-468.

6. Hoffmann M, Mada M, Carpenter TA, Sawiak SJ, et al. Additional sampling directions improve detection range of wireless radiofrequency probes. Magn. Reson. Med. 2016;76(3):913-918.

7. Tisdall MD, Hess AT, Reuter M, et al. Volumetric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI. Magn. Reson. Med. 2012;68(2):389-399.

8. Friston KJ, Ashburner J, Frith CD, et al. Spatial registration and normalization of images. Hum. Brain Mapp. 1995;3(3):165-189.

9. Jenkinson M, Beckmann CF, Behrens TE, et al. FSL. NeuroImage 2012;62(2):782-790.

10. Kim B, Boes JL, Bland PH, et al. Motion correction in fMRI via registration of individual slices into an anatomical volume. Magn. Reson. Med. 1999;41:964-72.

11. Jenkinson M. Measuring Transformation Error by RMS Deviation. FMRIB Analysis Group Technical Reports. 1999. http://fsl.fmrib.ox.ac.uk/analysis/techrep/tr99mj1/tr99mj1/. Accessed September 29, 2016.

Figures

Figure 1: (A) The simulated pulse sequence showing the timing of the navigator signal acquisition. In practice, this could be replaced by any motion indicator such as an optical camera, wireless probe, etc. (B) Resulting simulated image slice. (C) A slice from a patient dataset acquired with identical sequence specifications.

Figure 2: Typical motion correction results. The images shown in each column correspond to the same low, medium and high motion dataset, respectively.

Figure 3: RMSD for each correction method across datasets with (A) low, (B) medium and (C) high motion. The data shown in each graph were normalised separately. Error bars indicate standard deviations.

Figure 4: Comparison of typical simulated and detected translations (x) and rotations (θ) from a dataset with medium motion.

Figure 5: RMS deviation between the injected motion and slice-wise transforms estimated by each registration algorithm across datasets with (A) low, (B) medium and (C) high motion. Error bars indicate standard deviations. Note the adjustment of each horizontal axis for clear comparison between each scale of motion.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1297