Purpose

MRI Motion correction using optical tracking is increasingly popular [1]. A fundamental step in this process is transforming camera space co-ordinates to MR space. This transform is estimated from a calibration involving various poses recorded in the camera and MR reference frame simultaneously. We investigated the effect that translational and rotational errors in estimates of the poses, and the number of poses have upon the resulting calibration, and the impact that the resulting calibration errors have on recorded motions.

Methods

Poses in the camera reference frame and a calibration transform were simulated to produce corresponding poses in the MR reference frame. Random translational and rotational errors were then added to the MR poses. A non-iterative method was used to obtain apparent calibration transforms [2] [3] using these erroneous MR poses. The RMSE of the apparent calibration transform was taken for both the translational and rotational components. Simulations ran for 1000 iterations for random errors and for data sets containing 4 to 12 poses. To establish the impact that calibration errors have on a subsequent motion estimates, a simulation was performed based on a typical calibration for a 7T Magnex/Nova RF coil combination and motions up to 50mm translation and 10° rotation. Translational and rotational errors were then added to the calibration’s x and y components respectively, and the motion estimates resulting from the use of this ‘flawed’ calibration plotted against the true motions.

Results

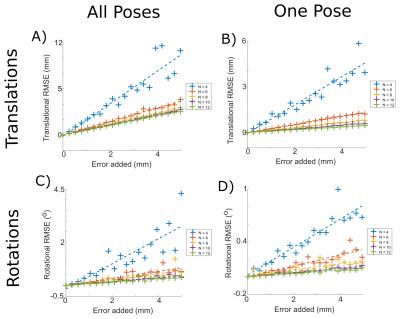
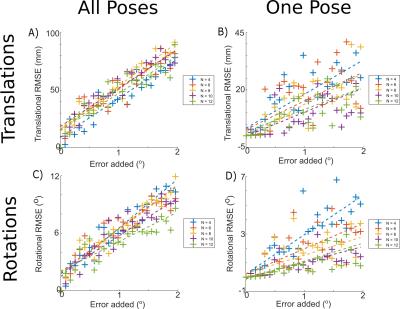
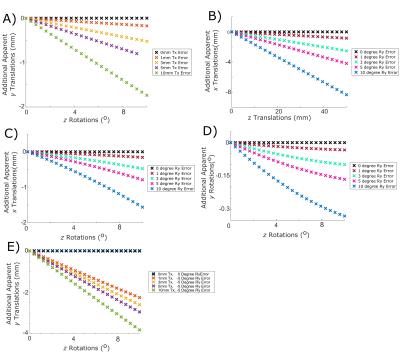
The max RMSE of the translational and rotational components of the calibration, for calibrations obtained using poses with translational errors are shown in Figure 1, either with an error in one pose (Figure 1B & 1D), or all poses (Figure 1A and 1C). The equivalent results for rotational errors in poses are shown in Figure 2. The use of flawed calibrations resulted in additional motions in different directions to the true motion, depending on the error in the calibration and the true motion (Table 1). Typical examples are shown in Figure 3. Rotational movements transformed using a translationally flawed calibrations resulted in small off-axis apparent translations. When translational movements were transformed using rotationally flawed calibrations, the resulting errors were greater than that of the translationally flawed calibration. Rotational movements resulted in additional apparent translational and rotational motions.

Discussion

Figure 1 shows that there was a linear relationship between the translational error in a pose and the error in the resulting calibration, with the error decreasing rapidly with increasing number of poses and little benefit in using more than 8 poses, whether the error is in one pose or all of them. The results were less clear for rotational errors in pose (Figure 2). In general increasing the number of poses increased the calibration accuracy except for the translation error resulting from errors in multiple poses (Figure 2A). This result was repeatable and suggests that the inclusion of additional poses with more errors decreases the stability of the calibration. Errors in a typical calibration resulted in apparent motions in different directions to the true motion, since motion in one axis is projected into another axis. Figure 3 shows translational calibration errors generally result in smaller translational errors than rotational calibration errors. From Figure 3 we can infer the permitted calibration errors necessary to correct movements to defined accuracies: smaller calibration errors are required to correct larger motions to the same accuracy as smaller motions. Table 2 outlines the maximum calibration error consistent with achieving reasonable motion correction for large movements found in clinical studies, and smaller motions in neuroscience studies. Table 2 also shows the approximate average and maximum pose errors to achieve these calibration accuracies, although this will vary with the number of poses. The calibration errors however have been approximated assuming either rotational or translational errors in calibration: comparing Figure 3A and 3E suggests that errors in calibration rotations can result in larger impacts from calibration translational errors, as such the numbers provided in Table 2 represent highest errors consistent with the stated accuracy, in practice more accurate calibrations will be required and this will be investigated by further monte carlo simulations of possible movements.

Conclusion

Errors in camera/MR calibrations leads to errors in motion estimates and may lead to reduced image quality by correcting for apparent rather than real motions. We suggest guidelines for necessary calibration error, assuming only translational or rotational errors in calibration. The translational errors in pose to achieve these calibration accuracies vary greatly with the number of poses unlike rotational errors in which more poses largely increases resistance to singular flawed poses.

Acknowledgements

This work was supported by funding from the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) [grant number EP/L016052/1].