Synopsis

The most promising techniques for understanding the biophysical basis of the MRI signals rely on combining multi-modal quantitative maps as a source of spatially-resolved information. If the MRI maps are not obtained from simultaneous acquisitions, they need to be co-registered in order to ensure a consistent localization of the signal sources for pixel-by-pixel fitting. However, the effects of the co-registration step are notoriously difficult to quantify. Here, we present a method for investigating the bias associated with co-registration for different quantitative MRI acquisitions, and outline the relevance of these biases for multi-parameter analysis.

Purpose

The quantitative analysis of biological tissues through MRI is a promising technique that aims at obtaining reliable and spatially-resolved microstructural information. Most of the methods rely on combining (semi-)quantitative information and correlating them to prior knowledge^1,2,3. Multi-parametric MR data acquisition can be performed:

1) separately⁴, i.e. each measurement is independent of each other;

2) simultaneously^5,6, i.e. the measurements of each parameter are intermixed.

In case of simultaneous acquisitions, if the effects of motion can be neglected, the location of the imaging sources is identical among the different images. Instead, for separate acquisitions, a (rigid) co-registration step is required to combine and bring the resulting maps to the same image space. This step however introduces biases related to the spatial interpolation at sub-voxel level and the inherently limited accuracy of the transformation matrix estimation. Here, we quantify the effects of sub-voxel or otherwise small mis-registration, as well as determining the minimum bias introduced by the co-registration step and compare them to the effect of a moderate increase in the noise level. Additionally, we discuss the different effects for common quantitative MRI maps.

Methods

Quantitative $$$T_1$$$, $$$T_2^*$$$ and magnetic susceptibility $$$\chi$$$ (QSM, obtained using SHARP and SDI⁷) maps (resolution: $$$0.6\;\mathrm{mm}$$$ isotropic) of the full brain were acquired in one healthy volunteer (female, age: $$$24\;\mathrm{yr}$$$), with a MAGNETOM 7T (Siemens, Erlangen, Germany) and a circularly-polarized Tx / 32-channels Rx Nova head coil. The quantitative images (with masked-out non-brain tissues) were compared to the same corresponding images after the application of:

1. translations in the axial direction for voxel offset values between $$$0.0$$$ and $$$1.0\;\mathrm{px}$$$;

2. rotations about the axial direction and centered in the geometrical center of the FOV for rotation angles between $$$0.0°$$$ and $$$1.0°$$$;

3. rotations followed by translations within the same value ranges as above;

4. addition of white noise, with standard deviations up to 10% of the dynamic range;

5. self-registration of the images after a large transformation, i.e. a $$$10\;\mathrm{px}$$$ offset followed by a $$$10°$$$ rotation.

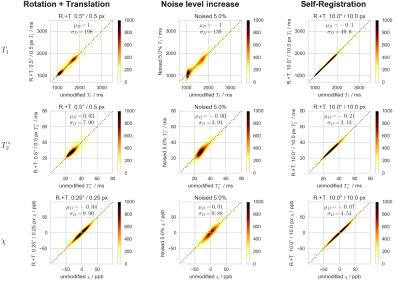
Results were assessed with voxel-by-voxel 2D histograms and by calculating the average, $$$\mu_D$$$, and the standard deviation, $$$\sigma_D$$$, of the difference images, obtained by subtracting the transformed images from the corresponding references. The $$$\mu_D$$$ and $$$\sigma_D$$$ parameters are both global measures reflecting the accuracy and precision (respectively) associated with a particular transformation. Additionally, we computed the squared Pearson's correlation coefficient, $$$r^2$$$, and the normalized mutual information, $$$nMI$$$, which indicate the linear and the general (both linear and non-linear) dependencies, respectively.

Results

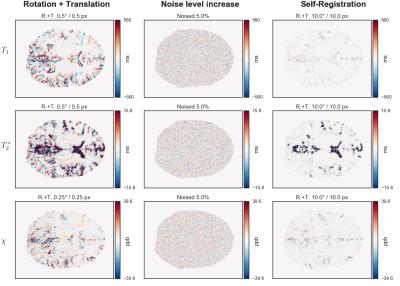
The difference images and the 2D histograms for selected transformations are shown for $$$T_1$$$, $$$T_2^*$$$ and $$$\chi$$$ maps in Figs.[1],[2], respectively.

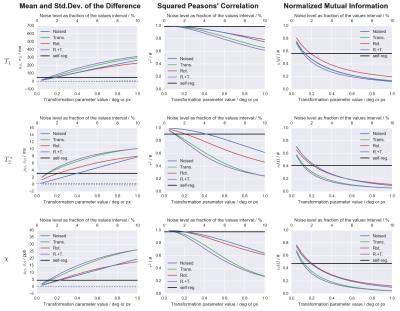
The correlation parameters are plotted against the considered transformations, including self-registration, in Fig.[3].

The tested transformations (both the ones associated with registration and the increase in noise level) may lead to significant degradation of precision ($$$\sigma_D$$$), but the accuracy ($$$\mu_D$$$) is largely unaffected.

Both $$$r^2$$$ and $$$nMI$$$ decrease for larger transformations, indicating a degradation in both linear and non-linear components of the dependency.

Discussion

The different behavior shown by the maps is primarily due to the inherent spatial variations of the observed values and/or to noise inherent to the acquisition.

The behavior of misregistrations towards the limit of no transformation indicates the robustness of a given map against such transformation.

The self-registration step gives a lower bound of the effects caused by the registration step. Larger effects should be expected because the co-registration of images with different noise should perform slightly worse compared to the self-registration.

Note that the $$$\mu_D$$$, $$$\sigma_D$$$, $$$r^2$$$ and $$$nMI$$$ parameters and the 2D histograms do not carry spatial information of the bias, and can be regarded as global measures. However, the spatial distribution of the intensities in the difference images varies, for each transformation, from very homogeneous for the noise level increase to remarkably non-homogeneous for the geometric transformations. In the latter case, the biases are more localized at the boundaries of relatively homogeneous regions, and can be large enough to cause the global measures to be comparable to at an increase in the noise level up to 10%.

Finally, the co-registration bias investigated here is only partially related to the motion of the sample during the acquisition, and motion correction techniques will have limited (if any) effect on it.

Conclusion

Acknowledgements

We would like to thank the Andreas Schäfer for providing some of the analysis tools and for helpful discussions. Funded by: EU through the 'HiMR' Marie Curie ITN (FP7-PEOPLE-2012-ITN-316716), the Max Planck Society through IMPRS NeuroCom, and the Helmholtz Alliance 'ICEMED'.

References

1. Stüber, C., Morawski, M., Schäfer, A., Labadie, C., Wähnert, M., Leuze, C., Streicher, M., Barapatre, N., Reimann, K., Geyer, S., Spemann, D., Turner, R., 2014. Myelin and iron concentration in the human brain: A quantitative study of MRI contrast. NeuroImage 93, Part 1, 95–106. doi:10.1016/j.neuroimage.2014.02.026

2. Rooney, W.D., Johnson, G., Li, X., Cohen, E.R., Kim, S.-G., Ugurbil, K., Springer, C.S., 2007. Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn. Reson. Med. 57, 308–318. doi:10.1002/mrm.21122

3. Schweser, F., Deistung, A., Lehr, B.W., Reichenbach, J.R., 2011. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism? NeuroImage 54, 2789–2807. doi:10.1016/j.neuroimage.2010.10.070

4. Weiskopf, N., Suckling, J., Williams, G., Correia, M.M., Inkster, B., Tait, R., Ooi, C., Bullmore, E.T., Lutti, A., 2013. Quantitative multi-parameter mapping of R1, PD*, MT, and R2* at 3T: a multi-center validation. Front. Neurosci. 7, 95. doi:10.3389/fnins.2013.00095

5. Ma, D., Gulani, V., Seiberlich, N., Liu, K., Sunshine, J.L., Duerk, J.L., Griswold, M.A., 2013. Magnetic resonance fingerprinting. Nature 495, 187–192. doi:10.1038/nature11971

6. Metere, R., Möller, H.E., Krüger, G., Kober, T., Schäfer, A., 2015. Simultaneous Quantitative Mapping of T1, T2*, and Magnetic Susceptibility with Multi-Echo MP2RAGE at 7 T, in: #0439. Presented at the ISMRM 23rd Annual Meeting & Exhibition, Toronto, Canada.

7. Schweser, F., Deistung, A., Sommer, K., Reichenbach, J.R., 2013. Toward online reconstruction of quantitative susceptibility maps: Superfast dipole inversion. Magn Reson Med 69, 1581–1593. doi:10.1002/mrm.24405