1270
Interpreting age-related changes based on the mean signal diffusion kurtosis1Cognition and Brain Sciences Unit, MRC, Cambridge, United Kingdom
Synopsis
Previous studies have shown that measures of non-Gaussian diffusion from diffusion kurtosis images (DKI) provide unique information on age-related tissue changes. In this study, a novel non-Gaussian diffusion index invariant to the distribution of fibres is proposed and applied to 650 datasets from the Cam-CAN ageing project. The results show that the proposed biomarker is not only applicable to any tissue configuration but also less sensitive to noise and artefacts when compared to traditional DKI measures. Moreover, for white matter regions, age-related changes measured by this index seem to reflect axonal alterations likely related to axonal loss mechanisms.
Introduction
Several studies have shown that diffusion tensor imaging (DTI) measures are sensitive to age-related changes even if no alterations in structural MRI are observed1. However, these measures are known to be unspecific to particular biological features and fail to represent voxels that do not contain well aligned white matter fibres. Diffusion Kurtosis Imaging (DKI) is an expansion of DTI which offers a quantification of the diffusion non-Gaussian behaviour in biological tissues2,3. In the context of ageing, several studies showed that DKI’s non-Gaussian measures do not follow the same age-related patterns as DTI’s anisotropy measures4,5. Although some biological models were proposed to relate these changes to specific biophysical features6, this has only been achieved for limited white matter fibre architectures. In this study, we propose a novel diffusion-kurtosis index from the mean diffusion-weighted (DW) signal which is invariant for different fibre configurations. This novel technique is then applied to the data of the Cambridge Center for ageing and Neuroscience (Cam-CAN) project7. Our aim is to characterize white matter fibre changes, such as axonal or myelin loss, independently of fibre orientation differences across distinct brain regions. For a meaningful interpretation, the age-related changes obtained with the novel kurtosis index are related to the axonal water fraction (AWF) and tortuosity (T) measures provided by the White Matter Tract Integrity (WMTI) model in regions where this model is valid6.Methods
Estimating the mean signal kurtosis: the mean signal attenuation $$$\left\langle E(b)\right\rangle$$$ along $$$N_g$$$ diffusion-weighted gradient directions, $$$n_j$$$, can be represented as a sum of $$$N_s$$$ signal contributions each characterized by an individual diffusion coefficient $$$D_i$$$ and volume fraction $$$f_i$$$. In analogy to DKI, this equation can be approximated to the cumulant expansion’s fourth order moments8:
$$$\left\langle E(b)\right\rangle=\frac{1}{N_g}\sum_{j=1}^{N_g}\sum_{i=1}^{N_s}f_i\exp[-bD_{i}(n_j)]\approx \exp[-b\left\langle d\right\rangle+\frac{1}{6}b^2\left\langle d\right\rangle^2\left\langle k\right\rangle]$$$ (Eq.1)
From Eq.1, the mean diffusion-kurtosis index $$$\left\langle k\right\rangle$$$ (or MDKI) can be estimated from $$$\left\langle E(b)\right\rangle$$$ samples which are known to be invariant to the fibre orientation distribution9– thus, $$$\left\langle k\right\rangle$$$ is independent of fibre configuration. In this study, Eq.1 is fitted using a weighted linear least squares approach (weights=$$$N_g(b)\times\left\langle E(b)\right\rangle$$$). This technique is evaluated using previously proposed multi-compartmental simulations3.
MRI experiments: DW datasets were acquired for 650 subjects (318 males) aged between 18 and 89 years on a 3T Trio Scanner (32channel coil) using a TRSE sequence to suppress eddy-current artefacts (30 directions for bvalues=1000,2000s.mm2 and three repetitions for b-value=0)7.
Data processing: To avoid partial volume effects from Gaussian smoothing, MRI noise is suppressed using a recently proposed PCA denoising technique10, while Gibbs artefacts are removed using local subvoxels-shifts11. Correction of volume misalignments due to motion and exclusion of datasets highly corrupted by intra-volume motion artefacts was performed following previous Cam-CAN studies12. The estimates obtained for MDKI, DKI’s mean kurtosis (MK), DTI’s fraction anisotropy(FA), and WMTI are evaluated on JHU white matter ROIs13.
Results
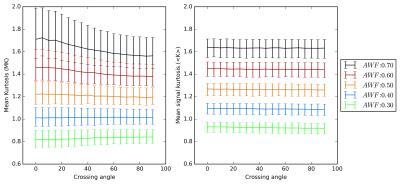
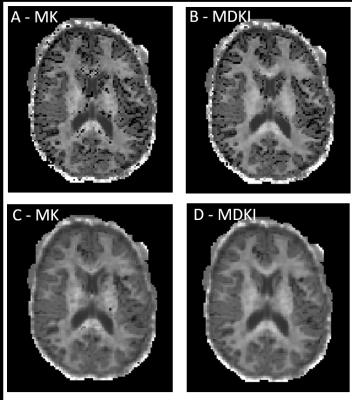
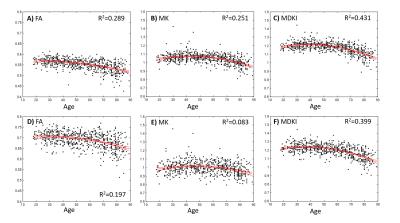
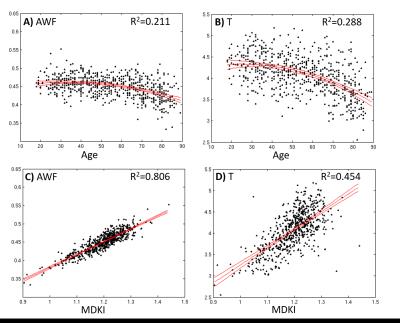
MK and MDKI values as a function of the intersection angle between simulated crossing fibres are shown in Fig.1 for different per fibre axonal volume fractions. MDKI and MK in vivo measurements for a representative subject are shown in Fig.2. The subjects’ mean FA, MK and MDKI age-profiles are plotted in Fig.3, while the correlations between MDKI and WMTI measures for regions of well aligned fibres (corpus callosum) are shown in Fig.4.Discussion
As expected, simulations show that MDKI depends on fibre features such as the axonal volume fractions, but not on properties related to fibre architecture, such as the angle of crossing fibres (Fig.1). Relative to MK, the MDKI is also shown to be less sensitive to the effects of noise in both simulations(Fig.1) and in vivo data(Fig.2). Moreover, in contrast to MK, no underestimations of MDKI are visually observed on the white matter regions of the in-vivo data (Fig.2, panels B and D). Similarly to MK, MDKI does not show a decrease with age until the fourth decade, while FA decreases from the early 20s(Fig.3). The mean MDKI along well-aligned corpus callosum regions shows a strong correlation with AWF, suggesting that MDKI age-related changes might reflect alterations in axonal water fraction (Fig.4), which are likely related to axonal loss14.Conclusion
It was shown that non-Gaussian measures from the mean DW signal can provide robust microstructural inferences that are applicable to any white matter fibre configurations. Particularly, in the context of ageing, measures of MDKI seem to be associated with axonal loss mechanisms. In future studies, MDKI can be used to study associations between microstructural and cognitive domain function age-related changes. Moreover, we expect that MDKI can also provide new insights for studies on psychiatric or neurological brain disorders.Acknowledgements
This work was funded by Fundação para a Ciência e Tecnologia FCT/MCE (PIDDAC) under grant SFRH/BD/89114/2012.
In vivo data were provided by the Cambridge Center for ageing and Neuroscience (Cam-CAN) project funded by the Biotechnology and Biological Sciences Research Council under grant BB/H008217/1.
References
[1] Moseley, M. Diffusion tensor imaging and aging – a review. NMR in Biomedicine 2002; 15(7-8): 553–560. doi:10.1002/nbm.785.
[2] Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional Kurtosis Imaging: The Quantification of Non-Gaussian Water Diffusion by Means of Magnetic Resonance Imaging. Magnetic Resonance in Medicine 2005; 53: 1432-1440. doi: 10:1002/mrm.20508.
[3] Henriques RN, Correia MM, Nunes RG, Ferreira HA. Exploring the 3D geometry of the diffusion kurtosis tensor—Impact on the development of robust tractography procedures and novel biomarkers. NeuroImage 2015; 111: 85-99. doi: 10.1016/j.neuroimage.2015.02.004.
[4] Falangola MF, Jensen JH, Babb JS, Hu C, Castellanos FX, Di Martino A, Ferris SH, Helpern JA. Age-related non-Gaussian diffusion patterns in the prefrontal brain. Journal of Magnetic Resonance Imaging 2008; 28(6): 1345–1350. doi:10.1002/jmri.21604
[5] Coutu JP, Chen JJ, Rosas HD, Salat DH. Non-Gaussian water diffusion in aging white matter. Neurobiology of Aging 2008; 35(6): 1412-1421. doi: 10.1016/j.neurobiolaging.2013.12.001.
[6] Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusion kurtosis imaging. NeuroImage 2011; 58: 177-188. doi: 10.1016/j.neuroimage.2011.06.006.
[7] Taylor JR, Williams N, Cusack R, Auer T, Shafto, MA, Dixon M, Tyler LK, Cam-CAN, Henson RN. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. NeuroImage 2015 (In Press). doi: 10.1016/j.neuroimage.2015.09.018.
[8] Kiselev VG. The Cumulant Expansion: An Overarching Mathematical Framework For Understanding diffusion NMR. In: Diffusion MRI: Theory, Methods and Applications, ed. Jones DK. Oxford University Press 2011, ISBN: 9780195396779.
[9] Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magnetic Resonance in Medicine 2016; 75: 1752–1763. doi: 10.1002/mrm.25734.
[10] Veraart J, Novikov DS, Sijbers J, Fieremans E. Denoising of diffusion MRI data using Random Matrix Theory. Proceedings of the 24th Annual Meeting of the International Society for Magnetic Resonance Medicine; Singapore. May 7–13, 2016.
[11] Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance in Medicine 2016; 76(5): 1574-1581. doi: 10.1002/mrm.26054
[12] Henriques RN, Cam-CAN, Correia MM. Reducing inter and intra-volume instabilities on diffusion-weighted data for ageing studies. Proceedings of the 22nd Annual Meeting of the Organization of Human Brain Mapping; Geneva, Switzerland. June 26–30, 2016.
[13] Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A, Woods R, Toga AW, Pike GB, Neto PR, Evans A, Zhang J, Huang H, Miller MI, van Zijl P, Mazziotta J. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. NeuroImage 2008; 40(1): 570-582. doi: 10.1016/j.neuroimage.2007.12.035
[14] Fieremans E, Jensen JH, Helpern JA, et al. Diffusion distinguishes between axonal loss and demyelination in brain white matter. Proceedings of the 20th Annual Meeting of the International Society for Magnetic Resonance Medicine; Melbourne, Australia. May 5–11, 2012.
Figures