1261
High-Resolution 4D Real-Time Phase-Contrast Flow MRI with Sparse Sampling1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, People's Republic of China, 2Martinos Center for Biomedical Imaging, Harvard Medical School, Chalestown, MA, United States, 3Vascular Imaging Laboratory, Department of Radiology, University of Washington, Seattle, WA, United States
Synopsis
This work presents a model-based imaging method, which integrates low-rank modeling, sparse modeling with parallel imaging, to enable 4D real-time phase-contrast flow MRI without ECG gating and respiration control. The proposed method achieves real-time imaging at a spatial resolution of 2.4 mm, temporal resolution of 35 ms, with three directional flow encodings, and well resolves beat-by-beat flow variations, which cannot be achieved by the conventional cine-based method. The proposed has been evaluated by in vivo data with multiple healthy subjects and one arrhythmic patient. For the first time, we demonstrate the feasibility of real-time 4D PC flow MRI.
Introduction
Conventional phase-contrast (PC) flow MRI relies on electro-cardiogram (ECG)-synchronized cine acquisitions and respiration control to assess blood flow dynamics [1, 2]. This often has relatively low acquisition efficiency and is not able to assess blood flow variabilities (e.g., in patients with cardiac arrhythmias). Real-time imaging without ECG gating and respiration control is a promising technique to overcome these limitations [3, 4], however, it results in a significantly more challenging reconstruction problem associated with highly-undersampled data. While a number of methods have been developed to enable real-time PC-MRI only in two spatial dimension (2D) with one velocity encoding [5-7], real-time 4D flow MRI has not been reported yet. In this abstract, we present a novel model-based imaging method, which integrates low-rank modeling, sparse modeling with parallel imaging, to achieve, for the first time, high-resolution 4D real-time phase-contrast flow MRI. The performance and utility of the proposed method has been evaluated by in vivo experiments with multiple healthy subjects and one arrhythmic patient.Theory & Methods
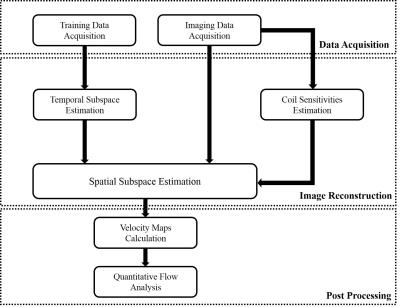
Due to strong correlation of flow imaging data along spatial, temporal, and flow encoding directions, the joint Casorati matrix $$${\bf{C}}=[\begin{array}{*{20}{c}}{{{\bf{C}}_1}}& \cdots &{{{\bf{C}}_{{{\rm{N}}_v}}}}\end{array}]$$$ is often approximately low-rank [8]. Here, we enforce an explicit rank constraint via matrix factorization [9,10], i.e., $$${\bf{C}}={\bf{UV}}$$$, where $$${\bf{U}}\in{{\Bbb C}^{N \times L}}$$$ and $$${\bf{V}}\in{{\Bbb C}^{L \times M}}$$$. Note that the columns of U and rows of V respectively span the spatial subspace and temporal subspace of C. Furthermore, we pre-determine the temporal subspace V from the temporal training data. Besides, the joint Casorati matrix often admits sparse representation in the spatial-spectral domain [11,12]. With the above low-rank and sparsity constraints, the image reconstruction problem can be formulated as $${\bf{\hat U}} = \arg \mathop {\min }\limits_{\bf{U}} \sum\limits_{i = 1}^{{{\text{N}}_c}} {\left\| {{{\bf{d}}_i} - \Omega \left[ {{{\bf{F}}_s}{{\bf{S}}_i}\left( {{\bf{U\hat V}}} \right)} \right]} \right\|_2^2} + \lambda {\left\| {vec\left( {{\bf{U\hat V}}{{\bf{F}}_t}} \right)} \right\|_1},$$ where $$${{\bf{d}}_i}$$$ denotes the measured (k, t)-space data, $$$\Omega $$$ is the sparse sampling operator, $$${{\bf{F}}_s}$$$ and $$${{\bf{F}}_t}$$$ respectively the spatial and temporal Fourier transform matrix, and $$${{\bf{S}}_i}$$$ the sensitivity map. After image reconstruction, the velocity maps of all the three directions can then be determined. Here, we include a diagram in Fig. 1 to illustrate the procedure of the proposed method.
We performed 4D real-time flow imaging experiments using the proposed method, in which five healthy volunteers and an arrhythmic patient were recruited. For comparison, we also acquired 4D cine flow imaging data with 2x SENSE [13]. All the scans were performed on a 3.0 T Philips scanner with a 32-channel cardiovascular coil. Both cine and real-time experiments were conducted on the whole aorta during free breathing with the following parameters: FOV = 180 × 256 × 43 mm3 (FH/AP/RL), spatial resolution = 2.4 × 2.4 × 2.4 mm3, matrix size = 76 × 108 × 18, repetition time/echo time = 4.4/2.6 ms, flip angle = 5°, and encoding velocity = 200/150/150 cm/s (FH/AP/RL), and temporal resolution is 35 ms.
Results
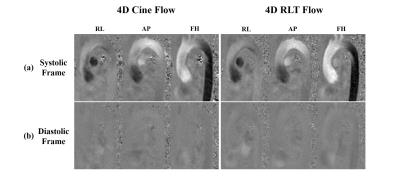
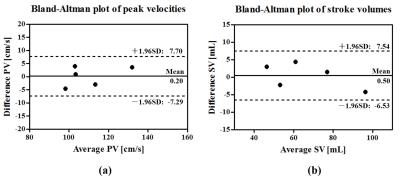
Fig. 2 show the reconstructed velocity maps from 4D cine flow imaging and the proposed real-time imaging method for a healthy subject. As can be seen, the proposed method provides comparable quality to the cine flow imaging method. Fig. 3 (a) and (b) respectively show the reconstructed flow profile associated with the ascending aorta and descending aorta for this subject. As can be seen, the proposed method is able to resolve flow variations. We further averaged flow profiles from the proposed 4D real-time imaging method over 10 cardiac cycles, and compared it with the one from the cine acquisition. As is shown in Fig. 3 (d) and (e), the flow profiles from the proposed method well correlates with the one obtained from the cine flow imaging method, which is highly desirable. Moreover, the Bland-Altman analysis of the peak velocities and stroke volumes are shown in Fig. 4 for all subjects, which further confirms the excellent agreement between the two methods. With respect to the experiment on the patient, the reconstructed flow profile and pathline visualization are shown in Fig. 5. Clearly, the proposed method well resolves the beat-by-beat pathological variations.Conclusions
This work presents a model-based imaging method to achieve, for the first time, high-resolution 4D real-time PC-MRI. The proposed method is capable to resolve the beat-by-beat physiological and/or pathological flow variations, which could not be achieved by conventional cine-based 4D flow MRI.Acknowledgements
The first and second authors contributed equally to this work. The authors thank Prof. Zhi-Pei Liang at the University of Illinois at Urbana-Champaign for useful discussions. This work was partially supported by Beijing Municipal Science & Technology Commission (No. Z131100005213001 and No. D111107003111007), and National Institute of Health (NIH-RO1-EB013695).References
[1] Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 4D flow MRI. J Magn Reson Imaging 2012;36:1015–1036.
[2] Dyverfeldt P, Bissell M, Barker AJ, Bolger AF, Carlhall CJ, Ebbers T, Francios CJ, Frydrychowicz A, Geiger J, Giese D, Hope MD, Kilner PJ, Kozerke S, Myerson S, Neubauer S, Wieben O, Markl M. 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson 2015;17(1):1-19.
[3] Joseph AA, Merboldt KD, Voit D, Zhang S, Uecker M, Lotz J, Frahm J. Real-time phase-contrast MRI of cardiovascular blood flow using undersampled radial fast low-angle shot and nonlinear inverse reconstruction. NMR Biomed 2012;25(7):917-924.
[4] Traber J, Wurche L, Dieringer MA, Utz W, von Knobelsdorff-Brenkenhoff, F, Greiser A, Jin N, Schulz-Menger J. Real-time phase contrast magnetic resonance imaging for assessment of haemodynamics: from phantom to patients. Eur Radiol 2016;26(4):986-996.
[5] Liu CY, Varadarajan P, Pohost GM, Nayak KS. Real-time color-flow MRI at 3 T using variable-density spiral phase contrast. Magn Reson Imaging 2008;26(5): 661-666.
[6] Joseph AA, Kowallick JT, Merboldt KD, Voit D, Schaetz S, Zhang S, Sohns JM, Lotz J, Frahm J. Real-time flow MRI of the aorta at a resolution of 40 msec. J Magn Reson Imaging 2014;40(1):206-213.
[7] Tan Z, Roeloffs V, Voit D, Joseph AA, Untenberger M, Merboldt KD, Frahm J. Model-based reconstruction for real-time phase-contrast flow MRI: Improved spatiotemporal accuracy. Magn Reson Med 2016.
[8] Liang ZP. Spatiotemporal imaging with partially separable functions. In: Proc. IEEE Int. Symp. Biomed. Imaging, 2007. pp. 988–991.
[9] Zhao B, Haldar JP, Brinegar C, Liang ZP, Low rank matrix recovery for real-time cardiac MRI. In: Proc. IEEE Int. Symp. Biomed. Imaging, 2010. pp. 996–999.
[10] Haldar JP, Liang ZP, Spatiotemporal imaging with partially separable functions: A matrix recovery approach. In: Proc. IEEE Int. Symp. Biomed. Imaging, 2010. pp. 716–719.
[11] Zhao B, Haldar JP, Christodoulou AG, Liang ZP. Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints. IEEE Trans Med Imaging 2012;31(9):1809-1820.
[12] Christodoulou AG, Zhang H, Zhao B, Hitchens TK, Ho C, Liang ZP. High-resolution cardiovascular MRI by integrating parallel imaging with low-rank and sparse modeling. IEEE Trans Biomed Eng 2013;60(11):3083-3092.
[13] Pruessmann KP,Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-962.
Figures