1259

Pushing the Boundaries of Low-Venc PC-MRI Acquisition Strategies with a Weighted, Regularized Optimization Reconstruction
Michael Loecher1 and Daniel B. Ennis1

1Department of Radiological Sciences, University of California, Los Angeles, CA, United States

Synopsis

We propose a novel reconstruction method for low-Venc (high-moment) PC-MRI reconstructions to allow for significant VNR gains while being more robust to the errors associated with these methods. The reconstruction accounts for unequal signal variances due to intravoxel dephasing, and includes constraints to account for residual phase wrapping errors. The method is tested in simulations, phantoms, and volunteers.

Introduction

4D phase contrast MRI (PC-MRI) acquisitions often suffer from low velocity-to-noise ratios (VNR) due to the high acceleration factors needed to acquire the large datasets in a clinically feasible scan time. Lowering the encoding velocity (Venc) increases VNR, however lowering Venc with traditional acquisitions leads to velocity aliasing when velocities exceed Venc. This aliasing limitation results in particularly low VNR for slow velocity regions in the same volume as high velocities, as occurs with systolic and diastolic flow, arterial and venous flow, or pathologies with localized high flow regions (stenoses, aneurysms).

To reduce Venc below the peak velocity and gain VNR, postprocessing unaliasing methods may be used to some degree, but for significant VNR gains, an alternate encoding strategy must be used to provide information to the unaliasing algorithm. The two most widely proposed encoding schemes to achieve this goal are dual Venc (DVenc) [1] and multi-directional high moment (MDHM) [2] methods. These methods allow for more significant reduction of Venc, but they also add new potential sources of error such as intravoxel dephasing and residual aliasing. These errors are not well understood or accounted for in the standard reconstruction and analysis.

The objective of this work was to evaluate a weighted and regularized optimization reconstruction to make low-Venc (high-moment) acquisition schemes more effective and robust. This was accomplished by including information about the gradient moments and signal estimates during reconstruction to simultaneously mitigate errors due to intravoxel dephasing and phase wrapping.

Theory

We solve for velocity ($$$\boldsymbol{v}$$$) by optimizing this non-convex equation:

$$\arg\min_{\boldsymbol{v}}{\left\|\boldsymbol{w}\left(e^{iA\boldsymbol{v}}-\boldsymbol{y}\right)\right\|_2^2}+\lambda\nabla^{2}\boldsymbol{v}\ subject\ to\ \left|\boldsymbol{v}\right|<v_{max}$$

where $$$\boldsymbol{y}$$$ is the magnitude normalized complex data vector, $$$A$$$ is the velocity encoding matrix, $$$v_{max}$$$ is the user defined velocity search radius (similar to Venc), and $$$\nabla^{2}\boldsymbol{v}$$$ represents a multidimensional Laplacian regularizer [3]. $$$\boldsymbol{w}$$$ is a data weighting factor equal to the velocity variance $$$\sigma_v^2$$$ with constant factors removed and calculated based on the signal magnitude and the prescribed first moments.

Methods

Computational fluid dynamics was used to simulate 20 phases of pulsatile blood flow through straight tubes of various diameters (2, 4, 6, and 8 mm) with a peak velocity set to 100 cm/s. Intravoxel dephasing was simulated by spatially oversampling the velocity profiles by 32x and using the DVenc and MDHM (7-point, ICOSA6 design) encoding schemes.

Data was collected in an aneurysm flow phantom and in the heads of eight (N = 8) healthy volunteers (with consent and IRB approval) using a stack of stars 4D-Flow sequence with a standard 4pt null encoding scheme (Venc=80 cm/s), as well as the DVenc (Venc=80,20 cm/s) and MDHM methods (Vencs=40cm/s and 20 cm/s). Scan times remained constant for all encoding schemes (8 minutes in the phantom, 12 minutes in-vivo). In the phantom experiments, velocity noise was estimated by calculating the standard deviation of velocity in static regions.

Velocities were solved using standard methods and proposed reconstruction, which was implemented using a multistart conjugate gradient descent method. In the simulated data, velocity error vectors were computed between the reconstructed and true velocity vectors. The mean magnitude of this error was reported.

Results

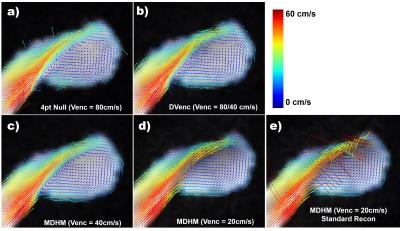
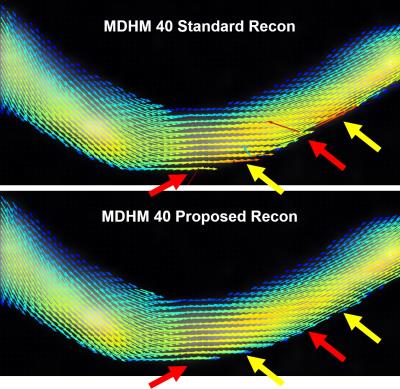
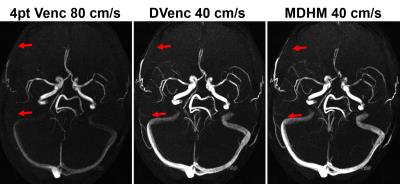
Figure 1 shows the results of the simulation experiment. Velocity errors across the vessels were reduced by 27.2%,36.4%,38.6%,40.3% for DVenc and 47.9%,69.1%,62.0%,62.5% for the MDHM in 2mm,4mm,6mm, and 8mm vessels. Figure 2 shows vector plots in the aneurysm flow phantom, where the reduction in noise and lack of artifact is more evident. Figure 3 shows the velocity noise estimates where significant gains with both he low-Venc methods are seen. Figure 4 shows the improvements of the proposed method where artifacts are eliminated. Figure 5 shows angiograms where the increase in VNR is apparent, despite constant scan times.

Discussion

The proposed reconstruction method leverages the use of additional noise estimations and constraints on velocity field continuity when solving for velocities with high moment acquisitions. The addition of weighting factors based on noise variance allows for a more accurate velocity reconstruction, particularly when certain velocity encodes are noisier than others, as often happens due to intravoxel dephasing. Constraints on the continuity of the velocity field were also added to reduce the presence of phase wrapping. This regularization is particularly important for the MDHM method, which is more VNR efficient than dual-Venc, but also more susceptible to these errors. These improvements are shown to make low-Venc acquisition strategies much more robust to noise and phase wrapping, allowing us to benefit from the increased VNR inherent to these acquisitions with fewer penalties or risk of artifacts.

Acknowledgements

Funding support from the Department of Radiological Sciences and Siemens Medical Solutions.

References

[1] Nett, E.J., Johnson, K.M., Frydrychowicz, A., Del Rio, A.M., Schrauben, E., Francois, C.J. and Wieben, O., 2012. Four-dimensional phase contrast MRI with accelerated dual velocity encoding. Journal of Magnetic Resonance Imaging, 35(6), pp.1462-1471.

[2] Zwart, N.R. and Pipe, J.G., 2013. Multidirectional high-moment encoding in phase contrast MRI. Magnetic Resonance in Medicine, 69(6), pp.1553-1563.

[3] Loecher, M., Schrauben, E., Johnson, K.M. and Wieben, O., 2015. Phase unwrapping in 4D MR flow with a 4D single-step laplacian algorithm. Journal of Magnetic Resonance Imaging.

Figures

Figure 1: Simulation results during peak velocity with DVenc and MDHM methods using Venc=30 cm/s. Velocity values for the standard and proposed reconstructions; fewer phase wrapped voxels are seen with the proposed reconstruction (top row). Phase errors are seen with both methods for the standard reconstructions, but are not present in the proposed reconstruction (bottom row).

Figure 2: Vector plots through a cross section of the aneurysm flow phantom showing the proposed reconstruction with various encoding strategies and Vencs. Qualitative assessment of the velocity fields showed improvements compared to the 4pt null images (a), particularly in slow flow regions. More improvement is seen with the MDHM methods (c,d) as compared to DVenc (b). No wraps or significant errors at the vessel walls are seen with the proposed reconstruction. Also shown is the standard reconstruction for a MDHM Venc=20cm/s acquisition where significant wrapping is seen (e). This error is corrected with the proposed reconstruction (d).

Figure 3: Standard deviation of velocity values in static ROIs of acquired data. Note that these datasets were all acquired in the same scan time, so despite the necessity for more velocity encodes and therefore more undersampling, a significant reduction in velocity standard deviation is seen with the low-Venc methods.

Figure 4: A portion of the right MCA in a volunteer acquired with the MDHM method and Venc = 40 cm/s. With the standard recon residual wrapping at vessel boundaries is seen, as pointed out with the red arrows. Yellow arrows point out errors that are the result of uncertainty due to intravoxel dephasing. All of these errors are eliminated or improved with the proposed reconstruction.

Figure 5: Reconstructed angiograms from a volunteer acquisition using the different encoding strategies. The higher moment acquisitions (DVenc and MDHM) show significantly better small vessel and venous signal with the proposed method, as shown with the arrows.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1259