1256
High-Resolution Phase Correction in Overdiscrete Spectroscopic Imaging Reconstruction using Piecewise Polynomial Interpolation1Technische Universität München, Munich, Germany, 2GE Global Research, Munich, Germany
Synopsis
A full phase correction at high resolution is incorporated into the overdiscrete reconstruction for 1H MR Spectroscopic Imaging (MRSI). This allows to correct spectral artifacts generated by phase disturbances and increase SNR in one step, hence improving metabolite detection for fast MRSI acquisitions at short echo times. The phase correction term is approximated as a piecewise polynomial, fitted from a water reference scan that is acquired simultaneously with the metabolite signal. The method was applied to standard phase encoded MRSI and Echo-Planar Spectroscopic Imaging (EPSI) brain scans showing comparable improvements.
Purpose
In Magnetic Resonance Spectroscopic Imaging (MRSI), short Echo Time (TE) acquisitions are of interest for SNR optimization. However, reliable metabolite detection is challenging at short TE due to the large and complex baseline and strong nuisance signals that can impair the metabolite signals. Moreover, fast encoding-efficient acquisitions such as Echo-Planar Spectroscopic Imaging1 (EPSI), involve rapid gradient switching leading to phase distortions from eddy currents and system vibrations. The overdiscrete reconstruction method has recently shown that a relevant gain in SNR can be achieved from coherent signal averaging and the cancellation of intravoxel noise correlation, performed at high resolution2,3. This step involves the correction of the temporal linear phase mainly caused by B0-field inhomogeneities. In this work, we propose a generalized phase correction for overdiscrete MRSI using spatiotemporal piecewise polynomial functions fitted from an unsuppressed water reference scan and interpolated to high resolution.Methods
In the overdiscrete reconstruction2,3,4, a high-resolution image is obtained by applying, to each temporal point of the acquired signal, the intermediate reconstruction operator $$F^{'}=\theta E^{H} (E\theta E^{H} + \alpha \Psi)^{+},$$ where E represents the encoding matrix, expressed at $$$\zeta^{2}$$$-fold of the nominal resolution, and correspond to a spatial weighting factor and the noise covariance matrix, respectively, and $$$+$$$ denotes the pseudo-inverse. The regularization parameter $$$\alpha$$$ controls the noise optimization. The correction for signal dephasing due to B0 inhomogeneities is applied in an intermediate step, obtaining $$$h_{corr}(\mathbf{r},t)=h(\mathbf{r},t)\cdot e^{-i2 \pi\cdot t \cdot \triangle f_{0}(\mathbf r)},$$$ where represents signal at the overdiscrete location and time , and to the local frequency shift in Hz. The final corrected signal can be further generalized to $$h_{corr}(\mathbf{r},t)=h(\mathbf{r},t)\cdot e^{-i2\pi\cdot \phi(\mathbf{r},t)}$$ , where the polynomial phase term $$$\phi(\mathbf{r},t)$$$ contains the zero-, first- and higher order phase components, corresponding, respectively, to the offset, off-resonance and eddy currents effects. The coefficients of the polynomial term are obtained from the water reference signal using weighted least squares $$p=(A^{T}W^{2}A)^{-1}A^{T}W^{2}\mathbf{y}$$ where $$$\mathbf{y}$$$ corresponds to the unwrapped phase of the measured water reference and $$$W$$$ to the weight matrix extracted from the magnitude of the reference signal. Finally, SRF is optimized and high resolution signals are averaged coherently4.5, by applying a Gaussian target function T.
Data acquisition: A standard phase encoded 2D-MRSI and a 2D-EPSI dataset of the brain of a healthy volunteer together with coil sensitivity profiles and a B0-field map for the same Field-of-View (FOV) were acquired using a 3T-HDxt system (GE Healthcare, Milwaukee, WI) with an 8-channel head receive coil (InVivo, Gainesville, USA). The acquisition parameters were: FOV=220x220x10mm3, voxel size=10x10x10mm3, TE/TR=35/1500ms, spectral bandwidth=1kHz, CHESS water suppression and PRESS volume localization. The unsuppressed water reference was measured between water-suppressed acquisitions using a low flip-angle excitation (FA=10°) in the same TR.
Data processing: The MRSI datasets were reconstructed using a (1) standard Fourier transform-based reconstruction and coil combination5, (2) overdiscrete reconstruction with B0 correction and eddy current correction at nominal resolution. (3) overdiscrete reconstruction with polynomial phase correction. For (2) and (3) the data was overdiscretized to a factor of and a Gaussian target function with $$$\sigma$$$=2 sub-voxels was used.
Polynomial interpolation: The fitting algorithm used the unwrapped phase of the spatially transformed water reference signal to fit polynomial functions within a temporal interval of 10ms. The fit was constrained to third order spatial and second order temporal basis functions.
Results and Discussion
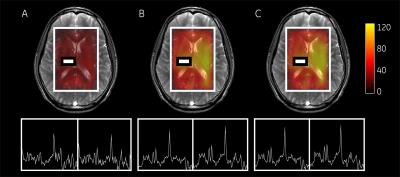
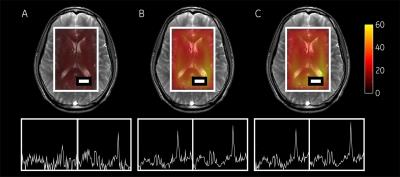
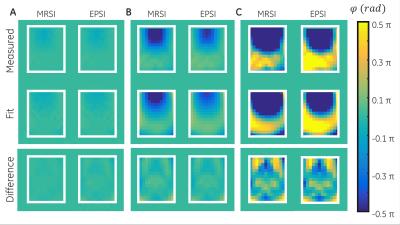
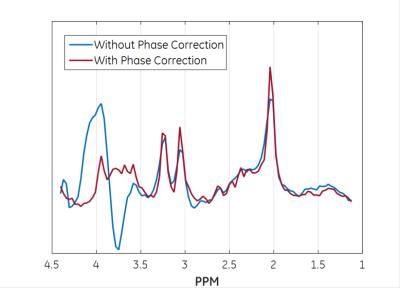
Fitting results for polynomials of third order show a negligible phase difference compared to the measured signal. Fig.-1 and Fig.-2 show the reconstructed phase encoded CSI and EPSI datasets, respectively. Improvements in spectral quality were observed and SNR enhancement was observed, with similar mean enhancement factors as reported in previous works4,6. the phase of the measured signal at different timepoints, the fitted polynomial term and the phase difference. Fig.-4 shows the benefits phase correction, reducing spectral artifacts mainly in the region between 4.5-3.5 ppm where metabolites of interest can be found.Conclusion
We demonstrated that phase variations, resulting from B0 inhomogeneities and eddy currents and system limitations, can be modeled as a spatially smooth piecewise polynomial function and use it as the high-resolution phase correction term in the overdiscrete reconstruction, obtaining the SNR enhancement and artifact removal of eddy current correction, with a single correction step. Moreover, the proposed acquisition allows to measure an unsuppressed water reference scan simultaneously with the metabolite signal resulting in a better correspondence between the correction terms and the MRSI dataset.Acknowledgements
No acknowledgement found.References
[1] Posse et al. High speed 1H spectroscopic imaging in human brain by echo planar spatial-spectral encoding. Magn Reson Med 1995; 33:34-40.
[2] Pruessmann K and Tsao J. Magnetic Resonance Imaging Method. US Patent No. 7.342.39.
[3] Kirchner et al. Reduction of voxel bleeding in highly accelerated parallel 1H MRSI by direct control of the spatial response function. Magn Reson Med 2014.
[4] Kirchner et al. Mechanisms of SNR and Line Shape Improvement by B0 Correction in Overdiscrete MRSI Reconstruction. Magn Reson Med 2015.
[5] Bydder et al. Optimal Phased Array Combination for Spectroscopy. Magn Reson Med 2010; 26(6): 847–850.
[6] Coello et al. Overdiscrete Reconstruction in Echo-Planar Spectroscopic Imaging with Auto Calibrated B0 Field Map Estimation. ISMRM 2016 #0386.
Figures