Introduction

Thermal equilibrium alignment of nuclear spins with the applied static magnetic field B₀ is the first step in conventional NMR and MRI signal generation¹. For ¹H in water this corresponds to the nuclear spin paramagnetic susceptibility χ_nucl^eq =μ₀M_z^eq/B₀ = μ₀μ_p²ρ_n/k_BT = 3.89 x 10^-9 ≈ 4ppb, at T=37°C. (M_z^eq is the longitudinal magnetization at equilibrium, μ₀ is the vacuum permeability, μ_p is the proton magnetic moment, k_B is the Boltzmann’s constant, and ρ_n is the ¹H spin density.) Because of its small magnitude, direct detection of longitudinal magnetization of nuclear spins (“longitudinal NMR”) usually requires sensitive magnetometers such as a SQUID^2,3. Here we show that nuclear susceptibility in fact makes a measurable shift in the MRI center frequency in a clinical scanner, and discuss its implications for MR-based quantitative susceptibility measurements.

Theory

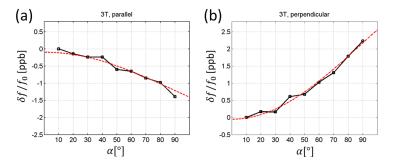
In a sequence with the repetition time (TR) much longer than T₁, the ¹H longitudinal magnetization immediately after the excitation is M_z^eq cosα where α is the tip-angle. This gives rise to the tip-angle dependent nuclear paramagnetic susceptibility χ_nucl= χ_nucl^eq cosα. The total tissue susceptibility is the sum of this and the electronic contribution, χ_tissue=χ_nucl+χ_elec where χ_elec≈ -9 ppm. Through χ_nucl, the tissue susceptibility in principle varies during and among MRI scans. χ_nucl gives rise to nuclear longitudinal polarization-dependent MR frequency shift, which we will call nuclear susceptibility shift (NSS). Similar to conventional susceptibility-induced B₀ inhomogeneity, NSS depends on the shape of the susceptibility boundary. For example, inside a thin slab with uniform susceptibility χ_nucl, the induced magnetic field is given by⁴ $$\delta B_{0,paral}=(1/3) B_0 \chi_{nucl} = (1/3) B_0 \chi_{nucl}^{eq} \cos\alpha \,\,\,\,\,\,\,\,\,\,(1)$$ when the slab’s face is parallel to B₀, but it is $$\delta B_{0,perp}=-(2/3) B_0 \chi_{nucl} = -(2/3) B_0 \chi_{nucl}^{eq} \cos\alpha \,\,\,\,\,\,\,(2)$$ when the face is perpendicular to B₀. Eqs.(1,2) include the Lorentz sphere effect⁵. NSS can be experimentally isolated from the bulk electronic susceptibility effect through tip-angle modulation.

Methods

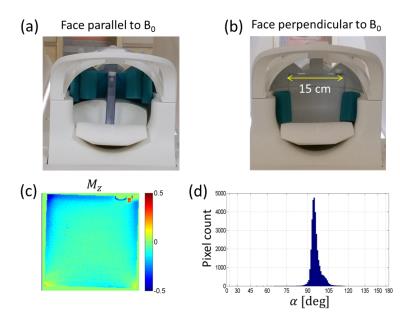
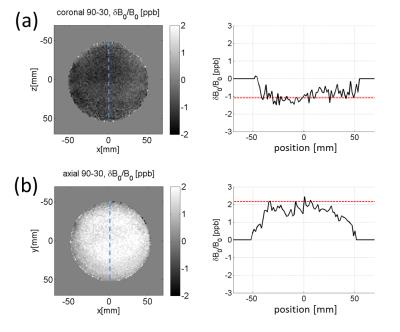
FID measurements. A flat square phantom filled with Gd-doped saline (T₁=700 ms) was prepared for scans at 3T (Siemens Prisma). The phantom was scanned at two different orientations, with its face parallel or perpendicular to B₀ (Fig. 1a,b). The scans consisted of free induction decay (FID) measurements without spatial encoding, at α=10° to 90°. Long TR (>5T₁) ensured full magnetization recovery. The FID time traces were apodized, zero-padded, and Fourier-transformed to determine the peak frequency with 3.8 mHz bin size. The main magnetic field drift was accounted for by measuring low-tip-angle FID signals every 1~2 minutes and subtracting the interpolated drift frequencies from the data. For each tip-angle, 4 to 8 FIDs were averaged in an interleaved manner. The B₀ drift during a typical measurement session (5~10 min) was a fraction of the range of the measured frequency variation. B₀ mapping. A 10-cm diameter spherical phantom with T₁=330ms was scanned at 3T for B₀ mapping on two different—axial and coronal—slices (thickness=5mm). A double-echo gradient echo sequence with TR= 1s, TE= 10,30ms was used. For each slice, B₀ maps were obtained with α=30° and 90°. Their difference, δB₀^90-30, served to test NSS in 2D.

Results

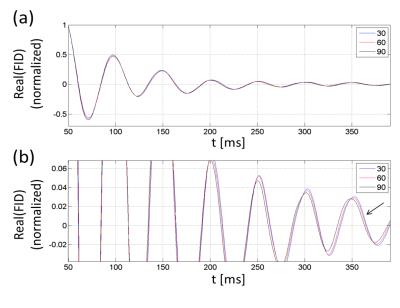
Figure 2 shows samples of FID signals (carrier at -20 Hz) at α=30°,60°,90° for the case when the flat phantom was parallel to B₀. A progressive phase shift is observed. The raw data were subject to magnet drift preventing accurate shift measurements. After the drift correction and averaging, the tip-angle dependent frequency shift was more clearly measurable (Fig. 3). As the phantom’s orientation changed, the sign of the tip-angle dependence reversed, and the magnitude of the shift was in good agreement with Eqs.(1,2) (after accounting for the slab's finite thickness by numerical dipolar field simulation). Figure 4 shows the B₀ map difference between α= 30° and 90° at two slice orientations. The sign of the B₀ change agrees with the theory. The shift amplitude was somewhat smaller than the theoretical predictions, potentially due to imperfect slice profile, tip-angle inhomogeneity, T₁ relaxation, and magnet drift during the B₀ map scan.

Disucssion

The high sensitivity of phase imaging in MRI allows measurement of thermal equilibrium nuclear spin polarization through its effect on the Larmor frequency in the imaged object. Given recent advances in quantitative susceptibility mapping (QSM)^6,7, nuclear susceptibility can potentially make difference in ppb-level tissue susceptibility quantification. Through a static (e.g., proton density) as well as dynamic effects (e.g., tip-angle non-uniformity, longitudinal relaxation, excitation profiles), NSS can also add uncertainties to high susceptibility-resolution QSM. With sufficient hardware stability, it may be possible to use NSS as an independent, dipolar-field-based method to measure proton density⁸.

Acknowledgements

This work was supported by IBS-R015-D1.