1205
Accelerated z-Spectrum Imaging1Biomedical Engineering, University of Calgary, Calgary, AB, Canada, 2Radiology, University of Calgary, Calgary, AB, Canada, 3GE Healthcare, Calgary, AB, Canada, 4Montreal Neurological Institute, McGill University, Montreal, QC, Canada
Synopsis
Long acquisition times preclude many potential applications of z-spectrum based imaging techniques, and have hindered their widespread use. Using SparseSENSE, a combined parallel imaging and compressed sensing acceleration technique, we present a method to reduce the acquisition time of z-spectrum images by a factor of 16. Z-spectrum images have been retrospectively undersampled to simulate 2-20× acceleration factors. Sparsifying reconstruction algorithms enable high quality image reconstructions for ambitious acceleration factors and are shown to maintain z-spectrum accuracy.
Purpose
Conventional MRI methods are insensitive to macromolecular content which suffer from sub-millisecond T2. z-Spectrum based imaging techniques, such as chemical exchange saturation transfer (CEST)1,2 and quantitative magnetization transfer (qMT)3, provide a means to investigate these molecules. For example, CEST enhances sensitivity to labile protons, and qMT targets macromolecular tissue content which strongly correlates with myelin in brain white matter4,5. Selective saturation of target molecules (restricted nuclei) create observable changes in free water nuclei via magnetization transfer. Plotting saturation as a function of offset frequency yields a characteristic z-spectrum, which can reveal detailed information beyond what can be seen from single saturation approaches (e.g. MT ratio). Unfortunately, the clinical translation of z-spectrum methods remains limited by long acquisition times. Recent work showed that compressed-sensing (CS) and parallel imaging (PI) techniques can considerably accelerate the acquisition time of CEST due to redundancies in the z-spectrum in the ~100Hz range6. Our work extends this method to show that shortened imaging times of the full z-spectrum required for qMT (~1–100 kHz) can be achieved using combined CS-PI.Methods
To induce magnetization transfer, an SPGR imaging sequence with a Fermi shaped off-resonance pulse was used to selectively saturate restricted nuclei. Fully sampled whole brain data was acquired in a single subject using a GE 3T 750 Discovery scanner and 32ch head coil (Nova Medical) with 2mm3 resolution. We acquired two unique z-spectra with effective saturation pulse flip angles 180° and 360° (4.9ms pulse duration), and a baseline volume with no saturation pulse. Both z-spectra were sampled at 15 offset frequencies logarithmically spaced between 1 and 10kHz, TR = 12ms, and an on-resonance excitation flip angle of 10°. Raw k-space data was saved for all acquisitions.
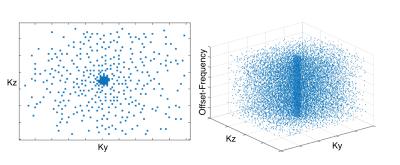
Retrospective k-space undersampling was performed on each z-spectra image to simulate 2-20× acceleration factors. Random undersampling is used to enforce incoherent signal aliasing, crucial for successful CS reconstruction7. To make use of combined CS-PI reconstruction algorithms, Poisson-disc sampling was chosen to prevent large sampling gaps, which minimizes noise and enables more efficient use of multi-coil array geometries8. Adapted for variable density sampling, an example of the random Poisson-disc sampling pattern used in this study is shown in Fig.1.
Undersampled data was reconstructed using a SparseSENSE method9. This technique modifies the Fourier operator of single channel CS reconstruction to include a coil sensitivity operator, $$$\text{S}$$$10. Using Matlab, images were reconstructed to minimize; $$$f(m)=||\text{F}_u\text{S}m-y||_2^2+\lambda_1||m-m_r||_1+\lambda_2||\Psi m|_1||+\lambda_3||\text{T}_v m||_1$$$ where $$$m$$$ is the final image, $$$y$$$ is undersampled k-space, and $$$\text{F}_u$$$ is the undersampled Fourier operator. Wavelet transform ($$$\Psi$$$), total variation ($$$\text{T}_v$$$) transforms are applied for spatial sparsity; a locally low rank reference image ($$$m_r$$$) promotes simple behaviour in the offset-frequency dimension. Regularization factors were set to $$$\lambda_1=0.001$$$, $$$\lambda_2=0.0005$$$, and $$$\lambda_3=0.0001$$$.
Results
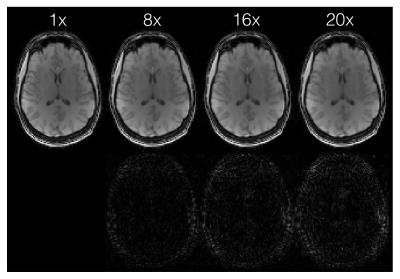
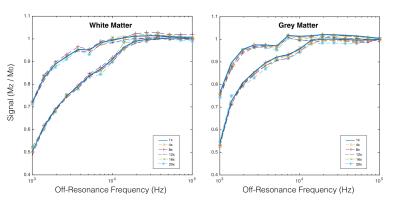
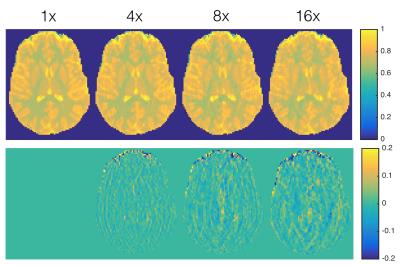
SparseSENSE reconstruction enables substantial acceleration of offset-frequency images (Fig.2). Images which have been undersampled by a factor of 16 or less exhibit minimal blurring of structural features, with only slight distortions visible at 20× acceleration. White matter (WM) and grey matter (GM) z-spectra were robust to signal fluctuations induced by acceleration (Fig.3). As z-spectroscopy relies on the saturation ratio from baseline, ratio images have been independently assessed for image degradation caused by acceleration (Fig.4). Reconstructed z-spectra and ratio image quality were assessed using the normalized mean squared error (NMSE) (Fig.5). Acceleration factors up to 16 maintain small NMSE values, however, a substantial jump in NMSE occurs at 20×.Discussion
Four-dimensional z-spectra data were shown to handle ambitious acceleration factors. Both the offset-frequency image in Figure 2 and the z-spectra in Figure 3 show good agreement between non-accelerated and accelerated protocols. Errors within each ROI increase with acceleration, and are slightly larger in GM than in WM, suggesting that GM regions may be more sensitive to reconstruction inaccuracies.
Ratio images are more sensitive to acceleration than their unmodified counterparts, with visible degradation present at all acceleration rates. Nonetheless, z-spectra have NMSE values significantly lower than ratio images they are based off of. These results demonstrate how undersampled data can yield accurate z-spectrum imaging with an immediate reduction in acquisition time.
Conclusion
Using SparseSENSE reconstruction, sampling requirements for the z-spectrum imaging protocol used in this study can be reduced by a factor of 16. With a fully sampled protocol duration of 38 minutes, prospective implementation at the proposed rate would result in a total protocol duration of 2.5 minutes. These results demonstrate the potential for image acceleration to have a substantial impact on the applicability of z-spectrum based imaging techniques such as CEST and qMT.Acknowledgements
The authors would like to recognize financial support from the Canadian Institutes of Health Research (FDN 143290) and the Campus Alberta Innovates Program.References
[1] Wolff SD, Balaban RS. NMR imaging of labile proton exchange. J. Magn.Reson. 1990; 86(1) 164-169. [2] Guivel-Scharen V, Sinnwell T, Wolff S, Balaban R. Detection of proton chemical exchange between metabolites and water in biological tissues. J. Magn.Reson. 1998; 133(1) 36-145. [3] Henkelman RM, Huang X, Xiang QS, et al. Quantitative interpretation of magnetization transfer. Man. Reson. Med. 1993; 29(1) 759-766. [4] Sled JG, Levesque I, Santos AC, et al. Regional variations in normal brain shown by quantitative magnetization transfer imaging. Man. Reson. Med. 2004; 51(2) 299-303. 5. Kucharczyk W, MacDonald P, Stanisz GJ, Henkelman RM. Relaxivity and magnetization transfer of white matter lipids in MR imaging: importance of cerebrorsis and pH. Radiology. 1994; 192(1) 521-529. [6] Heo HY, Zhang Y, Lee DH, et al. Accelerating chemical exchange saturation transfer (CEST) MRI by combining compressed sensing and sensitivity encoding techniques. Magn. Reson. Med. 2016. [7] Lustig M, Donoho D, Pauly JM. Sparse MRI: The aplication of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007; 58(6) 1182-1195. [8] Lustig M, Alley M, Vasanawala S, et al. L1SPIR-iT: autocalibrating parallell imaging compressed sensing. Proc. Soc. Magn. Reson. Med. 17. 2009; 379. [9] Bo L, Yi MZ, YingL. Sparsesense: application of compressed sensing in parallel MRI. International Conference on Information Technology and Applications in Biomedicine. 2008; 127-130. [10] King K. Combining compressed sensing and parallel imaging. Proc. Soc. Magn. Reson. Med. 16. 2008; 1488.
Figures