1203
Accurate, Rank-Adaptive Reconstruction of Undersampled Dynamic MRI Data Using Bayesian Information Criterion1Medical Physics, University of Wisconsin - Madison, Madison, WI, United States, 2Radiology, University of Wisconsin - Madison, Madison, WI, United States
Synopsis
Dynamic MRI must contend with imaging time limits imposed by physiological and physical constraints. Methods promoting low-rank solutions have become increasingly popular for dynamic MRI acceleration due to their ability to reconstruct from limited data. In this work we present a novel model-based reconstruction approach exploiting statistical machinery to spatially adapt the model to underlying signal. It overcomes deficiencies of low-rank techniques to preserve complex temporal dynamics of physiological processes.
Introduction
Dynamic MRI must contend with imaging time limits imposed by physiological and physical constraints. Methods promoting low-rank solutions have become increasingly popular for dynamic MRI acceleration due to their ability to reconstruct from limited data1-4. These techniques rely on the assumption that temporal signal can be approximated by a lower-dimensional model with3,4 or without1 a sparse residual. This assumption can be enforced either explicitly (by pre-selecting the rank1,4) or implicitly (through rank minimization2,3). However, restricting the model rank also promotes a low-rank solution which may compromise temporal fidelity and, ultimately, diagnostic information. Conversely, increasing the model rank rapidly deteriorates image quality as the constraining power subsides with the increase of model complexity4. In this work, we recognize that temporal behavior varies significantly in the object ranging from low (e.g., in static tissues) to more complex (e.g., due to contrast accumulation) to very complex (e.g., heart motion) dynamics. To accommodate these differences, we depart from the governing assumption of the previous techniques that the solution is dominated by low rank dynamics. Instead, we propose a new method, which spatially adapts model complexity during reconstruction to preserve high temporal fidelity while achieving high reconstruction quality compared to existing state-of-art techniques.
Theory
We demonstrate the new approach on the example of adapting MOdel Consistency COndition (MOCCO) reconstruction4. MOCCO finds image series $$$\bf{S}=\left(s(x_\rho,t_k)\right)\in\bf{C}^{n_p\times n_t}$$$ solving
$$\bf{S}=\arg\min_{\bf{S}}\left(\|vect(\bf{ES})-\bf{d}\|_2+\lambda\sum_\rho\|s_\rho\left(\bf{UH}_K\bf{U}^*-\bf{I}_t\right)\|_X\right)\qquad[1]$$
where $$$\bf{s}_\rho$$$ is the row of S corresponding to $$$\rho^{th}$$$ pixel, E is the joint encoding matrix for all $$$n_t$$$ time frames, d is a stacked vector of measured k-space data, $$$\bf{I}_t$$$ is $$$n_t\times n_t$$$ identity matrix. In case of context of data-driven low-rank reconstruction, comprises temporal principal components pre-estimated from fully-sampled k-space center. Diagonal filter matrix $$\left(\bf{H}_K\right)_{n,n}=\left\{\begin{array}{ll}1,& n\le K\\ 0, &\rm{otherwise}\end{array}\right.$$
selects the first K components from U to form a low-rank model.
In standard formulation, model order K is assumed to be low and spatially invariant. In our method, we avoid this assumption by allowing K to vary within the full range.To guide the selection of the model rank for a given pixel, we identify the minimal model order K sufficient for accurate representation of the pixel’s temporal dynamics utilizing the Bayesian information criterion (BIC)5. Namely, we create a nested sequence of models parametrizing them by their rank and estimating their posterior Bayesian probabilities using the BIC formulation adapted to dynamic imaging:
$$BIC(K,\bf{s})=n_t\ln\left(\|\bf{s}\left(\bf{UH}_K\bf{U}^*-\bf{I}_t\right)\|_2\right)+(K+1)\ln(n_t).\qquad[2]$$
The BIC measures model’s efficiency by estimating the likelihood of the data being described by the model (the first term) while penalizing its complexity K. As pixel dynamics are not known beforehand, we start with non-regularized solution of Eq. [1], determine model order for $$$\rho^{th}$$$ pixel as the one with minimum BIC value,
$$K_\rho=\arg\min_K{BIC}(K,\bf{s}_\rho),\qquad[3]$$
and then alternate solving Eq. [1] with BIC model order updates (Eq. [3]) until convergence.
Methods and Results
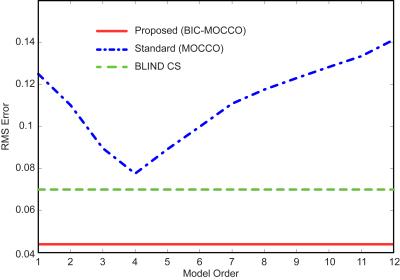
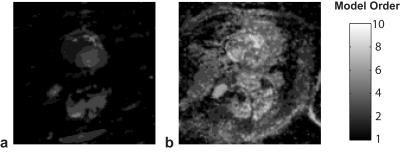
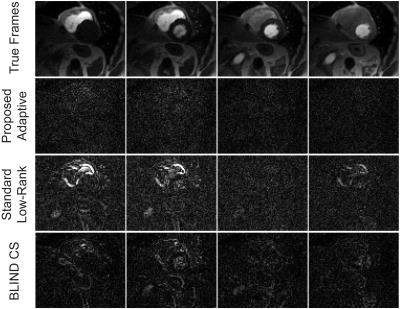
Dynamic contrast-enhanced myocardial perfusion data were acquired on 1.5T Siemens Sonata (saturation recovery TrueFISP, TR/TI=2.3/90 ms, FA=50°, R=2, 4 slices, 40 frames, 8-element coil). Cardiac CINE data were acquired on 1.5T Siemens Aera (prospectively triggered bSSFP breath-hold acquisition, TE/TR=1.56/3.1 ms, FOV=360x360 mm, 360x210 matrix, 26 phases, 32-channel array). The fully-sampled images were obtained by combining the coil images6 and subsampled k-space data (2D VD randomized sampling, acceleration factor R=4.3) were reconstructed using standard (non-adaptive) MOCCO4, the proposed rank-adaptive BIC-MOCCO and adaptive blind compressed sensing (BLIND CS)2. All reconstructions were optimized to yield minimized root-mean-squared errors (RMSE). Figure 1 shows RMSE plots for cardiac perfusion dataset. Proposed BIC-MOCCO results in the smallest RMS error followed by BLIND CS and standard MOCCO. Figure 2 demonstrates the spatial distribution of rank K after the first and third algorithm iterations (no reduction of RMSE detected afterwards). Figure 3 shows results of cardiac perfusion data reconstruction for representative frames. All techniques except proposed BIC-MOCCO produce significant structural errors. For cardiac CINE (Fig. 4), the proposed adaptive BIC-MOCCO demonstrated excellent preservation of temporal dynamics, which are significantly degraded by the non-adaptive method.Discussion
We presented a novel model-based reconstruction approach exploiting statistical machinery to spatially adapt the model to underlying signal. It overcomes deficiencies of low-rank techniques to preserve complex temporal dynamics of physiological processes. While our adaptation concept was illustrated with a low-rank technique, the ideas can be extended to other applications, including model-based parameter mapping, where multiple models may exist (e.g., in T2 mapping, single-exponent, two-exponent, and constant models to describe CSF, neural tissues, and background, respectively). Our ideas may also be adapted to methods employing direct parameter mapping for quantitative interpretation of accelerated dynamic contrast-enhanced MRI, and requiring different contrast kinetics models for different anatomies (vessels, heart, liver)7.Acknowledgements
This work was supported by NIH (R21EB018483, R01NS066982). We would like to thank Peter Kellman for providing the cardiac perfusion dataset and 2014 ISMRM Challenge for the cardiac CINE dataset.References
1. Liang ZP. Spatiotemporal imaging with partially separable functions. In: Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Washington, DC, USA, 2007. p 988–991.
2. Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging 2013;32:1132–1145.
3. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med, 2015; 73(3):1125:1136.
4. Velikina JV, Samsonov AA. Reconstruction of Dynamic Image Series from Undersampled MRI Data Using Data-Driven Model Consistency Condition (MOCCO). Magn Reson Med, 2015; 74(5):1279-1290.
5. Schwarz GE. Estimating the dimension of a model, Annals of Statistics, 1978; 6(2): 461–464.
6. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction ofphased array MR imagery. Magn Reson Med 2000;43:682–690.
7. Dikaios N, et al, Medical Image Analysis 01/2014; 18(7): 989-1001.
Figures