1201
General Phase Regularized Reconstruction with Phase Cycling1Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 2Department of Radiology, Stanford University, Stanford, CA
Synopsis
We present a general phase regularized image reconstruction method that is robust to phase wraps in initial solutions, with application to partial Fourier imaging, chemical shift imaging and flow imaging. The problem of constraining phase structures in reconstruction was studied under a regularized inverse problem framework. Since phase regularized reconstruction is inherently non-convex and sensitive to phase wraps in the initial solution, a reconstruction technique, named phase cycling, was proposed. The proposed method was applied to in vivo datasets and compared with state of the art reconstruction methods. The proposed phase cycling reconstruction provides an alternative way to perform phase regularized reconstruction, without the need of performing phase unwraping. It is robust to the choice of initial solutions and flexible to incorporate into different phase imaging applications.
Purpose
Phase variations in MRI can be attributed to a number of factors, including B0 inhomogeneity, chemical shift, fluid flow, and magnetic susceptibility. These phase structures provide opportunities in reconstruction to resolve undersampling artifacts or to extract additional information. In this work, we present a unified reconstruction framework to incorporate phase structures.
Since phase regularized image reconstructions are inherently non-convex and are sensitive to phase wraps in the initial solution, we propose a reconstruction technique, named phase cycling, that enables phase regularized reconstruction robust to phase wraps in initial solution. The proposed phase cycling technique is inspired by cycle spinning in wavelet denoising1 and phase cycling in bSSFP. Instead of unwraping phase before or during the reconstruction, the proposed phase cycling makes the reconstruction invariant to phase wraps by cycling different initial phase solution during reconstruction. Our key difference from existing works2-5 in phase image reconstruction methods is that the proposed phase cycling does not solve for the absolute phase, but rather averages out the effects of phase wraps.
Theory
To unify phase image reconstruction, we consider the following forward model:
$$y=A(Mm\cdot e^{jPp})+z$$
and the following (non-convex) regularized least squares objective function:
$$f(m,p)=\underbrace{\frac{1}{2}\|y-A\left(Mm\cdot e^{jPp}\right)\|_2^2}_{\text{Data consistency }f(m, p)}+\underset{\text{Regularization }g(m,p)}{\underbrace{\vphantom{\frac{1}{2}}g_m(m)+g_p(p)}}$$
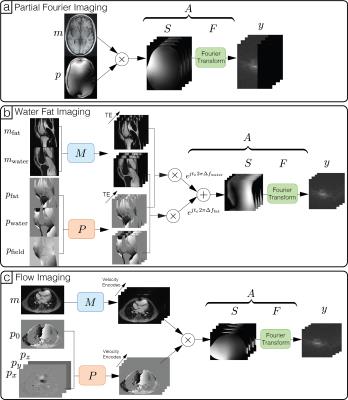
where $$$y$$$ is the acquired kspace measurements, $$$m$$$ and $$$p$$$ are the magnitude and phase images, $$$z$$$ is a noise vector, $$$A$$$ is the forward operator for the complex image, $$$M$$$ and $$$P$$$ are the forward operators the magnitude and phase images, and $$$\cdot$$$ is the point-wise multiplication operator. Figure 1 provides illustrations of how the above forward model can be adapted to various applications.
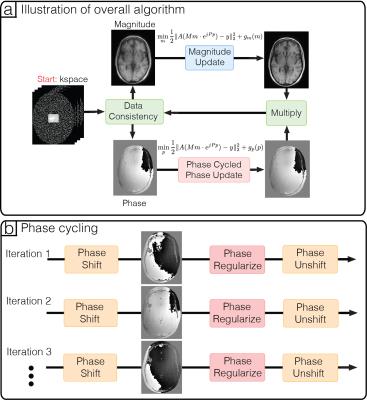
Alternating minimizing can be used to descend monotonically with respect to the objective function (Figure 2a). However, the result is very sensitive to the phase wraps in the initial solution. This is because phase wraps are highly discontinuous and phase regularization heavily penalizes these discontinuities, causing artifacts to accumulate over iterations.
To mitigate these artifacts from regularizing phase wraps, we propose a reconstruction technique, named phase cycling. We note that the position of phase wraps can be shifted spatially by adding a constant global phase, and artifacts caused by phase regularization also shifts spatially. Hence, if we shift the phase wraps randomly over iterations (Figure 2b), then the artifacts are effectively averaged spatially over iterations. This is an instance of inexact proximal gradient method6, which guarantees inexact convergence.
Methods
The proposed method was evaluated through applications on water-fat separation, partial Fourier and flow imaging.
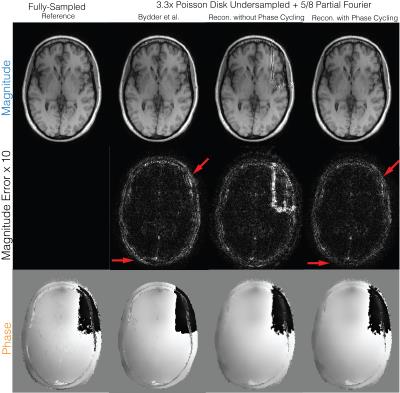
Partial Fourier (Figure 3): A fully-sampled human brain dataset was acquired on 1.5T GE Signa scanner with a 8-channel head coil, 3D GRE, image size of 256x256x230 and spatial resolution of 1mm. The dataset was retrospectively undersampled by 4 with a 24x24 calibration region and partial Fourier factor of 5/8. The proposed method with and without phase cycling were applied on the undersampled datasets. $$$\ell 1$$$ regularizations were imposed on the Daubechies wavelet domain for both magnitude and phase images.
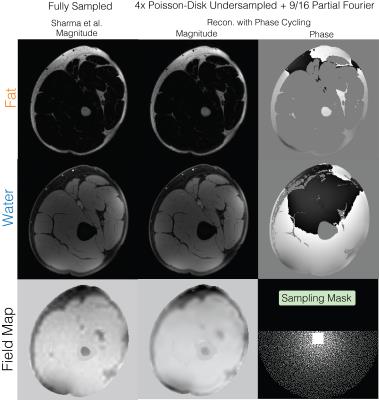
Water-fat+partial Fourier (Figure 4): A fully sampled upper-leg water-fat dataset was obtained from the water-fat toolbox8 and was acquired on a GE 3T Signa system, using an IDEAL squence with TE=[2.184,2.978,3.772] ms, BW=125kHz, 5 degree flip angle and a 256x256 sampling matrix. The dataset was retrospectively under sampled by 4 with 9/16 partial Fourier factor.
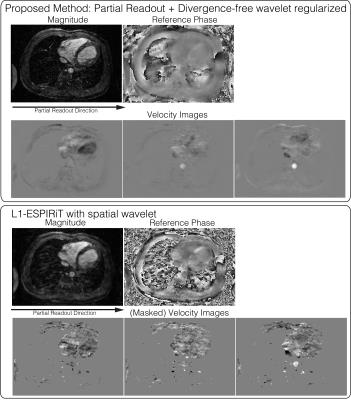
Divergence-free wavelet+partial Fourier (Figure 5): The proposed method was applied on a 4D flow dataset, with randomized velocity encode undersampling, VDRad undersampling pattern11 and a partial readout factor of 0.7. Divergence-free wavelet9, 10 regularization was imposed to enforce physical flow constraints on the velocity images.
Results
Partial Fourier (Figure 3): Without phase cycling, significant artifacts can be seen in the magnitude image near phase wraps in the initial solution. Reconstruction with phase cycling does not display these artifacts and has superior performance compared to Bydder et al.7
Water-fat+partial Fourier (Figure 4): Water-fat separation and partial Fourier were simultaneously performed using the proposed method with phase cycling and has similar quality as the fully-sampled water-fat images12.
Divergence-free wavelet+partial Fourier (Figure 5): The reconstructed magnitude image has no apparent blurring from partial readout, compared to the $$$\ell 1$$$ ESPIRiT13 result. We also note that the velocity images are not masked and that the velocities in low magnitude regions are naturally suppressed with the proposed reconstruction.
Discussion
Since the proposed method explicitly accounts for phase, different phase structures can be incorporated into reconstruction in a straightforward manner. In particular, conventional homodyne methods cannot be used with water-fat and 4D flow imaging because phase information is lost, whereas the proposed method easily generalizes to these applications.Acknowledgements
No acknowledgement found.References
[1] R. R. Coifman and D. L. Donoho, “Translation-invariant de-noising,” in Wavelets and Statistics. New York, NY, USA: Springer, 1995, pp. 125– 150
[2] Doneva M, Bornert P, Eggers H, Mertins A, Pauly J, Lustig M. Compressed sensing for chemical shift-based water-fat separation. Magnetic Resonance in Medicine 2010; 64:1749–1759.
[3] Sharma SD, Hu HH, Nayak KS. Accelerated water-fat imaging using restricted subspace field map estimation and compressed sensing. Magnetic Resonance in Medicine 2011; 67:650–659.
[4] Lu W, Hargreaves BA. Multiresolution field map estimation using golden section search for water-fat separation. Magnetic Resonance in Medicine 2008; 60:236–244.
[5] Zhao F, Noll DC, Nielsen JF, Fessler JA. Separate magnitude and phase regularization via compressed sensing. IEEE Transactions on Medical Imaging 2012; 31:1713–1723.
[6] Sra S. Scalable nonconvex inexact proximal splitting. Advances in Neural Information Processing Systems 2012; pp. 530–538.
[7] Bydder M, Robson MD. Partial fourier partially parallel imaging. Magnetic Resonance in Medicine 2005; 53:1393–1401.
[8] https://www.ismrm.org/workshops/FatWater12/data.htm
[9] Ong F, Uecker M, Tariq U, Hsiao A, Alley MT, Vasanawala SS, Lustig M. Compressed Sensing 4D Flow Reconstruction using Divergence-Free Wavelet Transform . In: 22nd Annual Meeting of ISMRM, Milan, Italy, May 2014 p. 0326.
[10] Santelli C, Loecher M, Busch J, Wieben O, Schaeffter T, Kozerke S. Accelerating 4D flow MRI by exploiting vector field divergence regularization. Magnetic Resonance in Medicine 2016; 75:115–125.
[11] J. Y. Cheng, K. Hanneman, T. Zhang, M. T. Alley, P. Lai, J. I. Tamir, M. Uecker, J. M. Pauly, M. Lustig, and S. S. Vasanawala, “Comprehensive motion-compensated highly accelerated 4D flow MRI with ferumoxytol enhancement for pediatric congenital heart disease,” J. Magn. Reson. Imaging, vol. 43, no. 6, pp. 1355–1368, Dec. 2015.
[12] S. D. Sharma, H. H. Hu, and K. S. Nayak, “Chemical shift encoded water-fat separation using parallel imaging and compressed sensing,” Magn. Reson. Med., vol. 69, no. 2, pp. 456–466, Apr. 2012.
[13] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magn. Reson. Med., vol. 71, no. 3, pp. 990–1001, May 2013.
Figures