1200
Extended Hybrid-SENSE: off-resonance and eddy corrected joint blip up/down reconstruction with reduced g-factor penalty1Stanford University, Stanford, CA, United States
Synopsis
Geometric distortions caused by off-resonant spins are a major issue in EPI based functional and diffusion imaging. We present a novel approach to the problem of geometric distortions. An extension of the model-based, algebraic hybrid-SENSE reconstruction method in combination with a known fieldmap, calculated from blip up/down scans, allows for correction of off-resonance effects during the reconstruction. This enables a joint blip up/down reconstruction that significantly reduces g-factor penalty if the blip-down trajectory is chosen to fill in missing k-space samples from the blip-up scan. The resulting high SNR images are automatically eddy-current corrected and geometric distortions are minimized.
Introduction
Geometric distortions caused by off-resonant spins are a major issue in EPI-based functional and diffusion imaging. Typically, correction methods use an off-resonance map and operate as a post-processing step on the magnitude images. A robust method to measure off-resonance maps is the blip up/down approach, where the polarity of the 2nd readout is inverted (2). Brain regions that are compressed in the blip-up acquisitions are stretched in the blip-down case and vice versa. From that, FSL’s topup implementation calculates the off-resonance map.
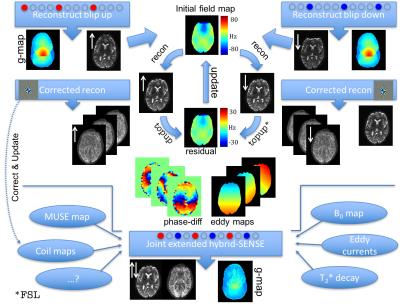
We present a novel two-stage approach to correct for geometric distortions that makes use of the blip up/down concept. First, we propose an extension of the model-based, algebraic hybrid-SENSE reconstruction method (1) that allows correction for off-resonance effects. For accelerated scans (SMS and/or in-plane) we then employ hybrid-SENSE for a joint blip up/down reconstruction where we choose the sampling pattern of the blip-down trajectory (Figure 4) such that it partly fills in missing k-space samples. A joint reconstruction not only benefits from signal averaging but also from reduced g-factor penalty because the effective acceleration factor is reduced.
Theory
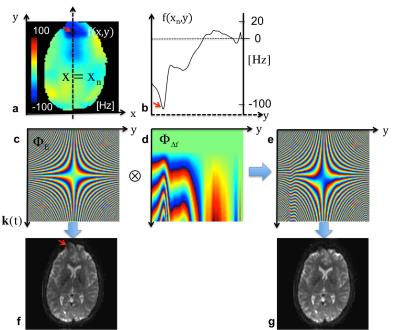
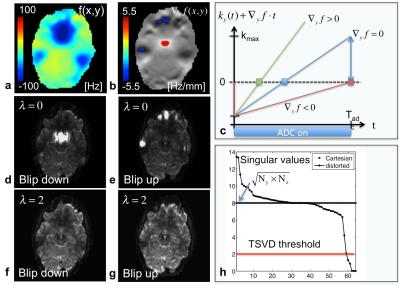
Ignoring off-resonance effects along the readout, and performing an FT along the $$$k_x$$$ domain, transforms the k-space data $$$s_0(k_x,k_y,k_z)$$$ to an hybrid space $$$ s(x,k_y,k_z) $$$. For every position $$$ x=x_n$$$ we can write the signal equation (forward model) in matrix notation as $${\bf s=Fm} \hspace{10mm} [1]$$ with the unknown magnetization $$$ {\bf m} \in \mathbb{C}^{N_yN_x \times 1} $$$ and the signal vector $$$ {\bf s} \in \mathbb{C}^{N_sN_c \times 1} $$$ that consists of all $$$N_s$$$ acquired ky-kz k-space samples times the number of receiver coils $$$N_c$$$. The effective encoding matrix $$$ \bf F= C \circ E \circ W \circ R $$$ with $$${ \bf C,E,W,R} \in \mathbb{C}^{N_s N_c \times N_y N_z} $$$ is the Hadamard product of the individual matrices that model the encoding process where: $$$\bf C$$$=coil sensitivity variation, $$$\bf E$$$=gradient encoding from$$$k_y$$$ and $$$k_z$$$-space, $$$\bf W$$$=off-resonance effects, and $$$\bf R$$$=intensity variations. In order to invert the rectangular matrix $$$\bf F$$$, we use a truncated singular value decomposition approach (TSVD) (3) where eigenvalues below a certain threshold $$$\lambda$$$ are completely suppressed (Figures 1,2). The solution is then given as $$ {\bf m = F}_{pinv}^{TSVD} {\bf s} \hspace{10mm} [2] $$
For the joint blip up/down reconstruction we rewrite the signal model as $${\bf F_{\uparrow \downarrow}}=\left(\begin{array}{c}{\bf F_{\uparrow}}\\ {\bf F_{\downarrow}}\end{array}\right) \hspace{10mm} [3]$$ where $$$\bf F_{\uparrow}$$$ and $$$\bf F_{\downarrow}$$$ are the effective encoding matrices for the blip up$$$(\uparrow)$$$ and down$$$(\downarrow)$$$ trajectories. The g-factor map is calculated as $$ g(x_n,y,z)=diag(\sqrt{\frac{{\bf F}_{pinv}^{TSVD}({\bf F}_{pinv}^{TSVD})^T}{{\bf C C}^T} })/\sqrt{R_{tot}} \hspace{10mm} [4]$$
where $$${\bf C C}^T$$$ corresponds to a SENSE reconstruction with R=1.
Methods
All measurements were performed at 3T using a 32-channel head coil. Reconstructions were performed off-line using MatLab. The “blip down”-EPI acquisition is implemented by inverting the phase encoding gradients while keeping all other parameters unchanged. The fieldmap was estimated using FSL5.0’s topup (http://fsl.fmrib.ox.ac.uk/fsl) with default parameters (4). For the joint reconstruction we employed a MUSE-like correction for phase inconsistencies between segments (5) and the workflow is displayed in Figure 5. The following parameters were used for blip up/down acquisitions with varying SMS and in-plane accelerations Ry: FOV=22x22cm, NxxNy=128x128, CAIPI blip-factor=2; partial Fourier=0.75, esp=0.55ms, slice thickness=2mm, TR=3s.Results
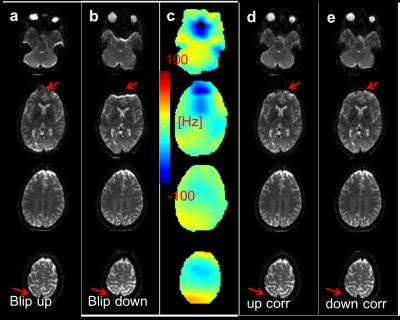
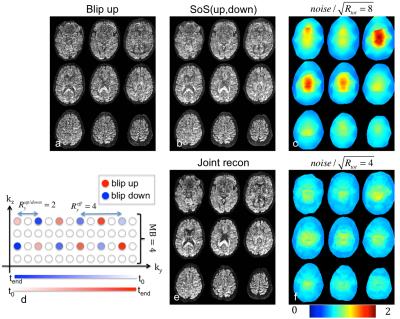
Figure 3 displays one reconstructed multi-band group (SMS-factor=4,Ry=1) for blip-up (a) and blip-down (b). From these two the fieldmap in c is derived and used in the off-resonance-corrected hybrid-SENSE reconstructions for blip-up (d) and -down (e). Figure 4 demonstrates the g-factor penalty reduction for the joint reconstruction of diffusion weighted (b=2000) acquisitions (SMS-factor=4, Ry=2). The off-resonance corrected blip-up reconstruction (red samples in d) is shown in a and the corresponding g-factor map for a total acceleration factor of Rtot=8 is displayed in c. Sum-of-squares combination of separate blip-up and -down reconstructions is displayed in b. Sum-of-squares combination does not affect the g-factor map from c. The joint blip up/down reconstruction (red and blue samples in d) in e has higher SNR than blip-up or sum-of-squares-combination. The corresponding g-factor map for Rtot=4 is shown in f.Discussion
Modelling off-resonances in an algebraic reconstruction framework results in images with significantly reduced geometric distortions. We have shown that regularization is important for regions where local off-resonance gradients oppose the gradients from k-space encoding (Figure 2). Acquiring blip-up/down scans for each diffusion direction allows for highly accurate estimation of dynamic off-resonances and eddy-current contributions. The longer scan time is more than compensated by the SNR increase due to averaging, the g-factor penalty reduction and the improved image quality.Acknowledgements
NIH (2R01 EB002711 , 5R01 EB008706, 5R01 EB011654), the Center of Advanced MR Technology at Stanford (P41 RR009784), Lucas Foundation.References
1. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage [Internet] 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7. 2. Zhu K, Dougherty R, Wu H, Middione M, Takahashi A, Zhang T, Pauly J, Kerr A. Hybrid-Space SENSE Reconstruction for Simultaneous Multi-Slice MRI. IEEE Trans. Med. Imaging [Internet] 2016. doi: 10.1109/TMI.2016.2531635. 3. Hansen PC. Truncated Singular Value Decomposition Solutions to Discrete Ill-Posed Problems with Ill-Determined Numerical Rank. SIAM J. Sci. Stat. Comput. [Internet] 1990;11:503–518. doi: 10.1137/0911028. 4. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23 Suppl 1:S208-19. doi: 10.1016/j.neuroimage.2004.07.051. 5. Chen N-K, Guidon A, Chang H-C, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage [Internet] 2013;72:41–7. doi: 10.1016/j.neuroimage.2013.01.038.Figures