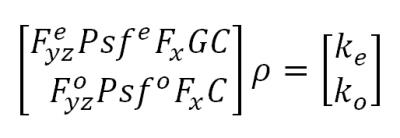1198
Echo-planar imaging with wave-CAIPI acquisition and reconstruction1Faculty of Psychology and Neuroscience, Maastricht University, Maastricht, Netherlands, 2Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, Boston, MA, United States, 4Fetal-Neonatal Neuroimaging & Developmental Science Center, Boston Children’s Hospital, Boston, MA, United States, 5Department of Medicine, John A. Burns School of Medicine, University of Hawaii, Honolulu, HI, United States, 6Harvard Medical School, Boston, MA, United States, 7Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
wave-CAIPI allows for high undersampling factors and hence acquisition speed-up in anatomical imagines sequences including 3D GRE, 2D SMS-TSE and MP-RAGE (3D TFL). The coil array’s full 3D sensitivity encoding is exploited, resulting in negligible g-factor penalties even in highly accelerated scans. Echo-planar imaging (EPI) sequences, both 2D and 3D EPI with Cartesian blipped-CAIPI have recently brought tremendous speed-up to BOLD and diffusion imaging in the neurosciences. We here explore the potential of going beyond blipped-CAIPI EPI by incorporating sinusoidal z- and y- gradient wave perturbations into the EPI readout. Initial results are shown for 3D wave-CAIPI EPI at 7T.
Purpose
To investigate the potential of wave-CAIPI acquisition in echo-planar imaging sequences.Introduction
wave-CAIPI has been shown to allow for considerable undersampling and acquisition speed-up in anatomical imaging sequences including 3D GRE [1], 2D SMS-TSE [2] and MP-RAGE (3D TFL) [3]. The method is an extension of the Cartesian slice and volumetric CAIPIRINHA first introduced by Breuer [4,5], and the addition of sinusoidal z- and y- gradient perturbations during the readout results in a 3D aliasing pattern that exploits a coil array’s full sensitivity encoding power [1,6]. Cartesian (blipped-)CAIPI by contrast utilizes only the two coil dimensions along the phase-encoding direction. Echo-planar imaging (EPI) sequences, both 2D-SMS [7] and 3D EPI [8], with Cartesian blipped-CAIPI [9] have recently brought tremendous benefits to the neurosciences, with great speed-up to the notoriously slow diffusion-weighted EPI [10], as well as BOLD- [7], perfusion- [11] and blood volume weighted [12] EPI. We here explore the potentials of going beyond blipped-CAIPI EPI in order to achieve higher acceleration factors at acceptable g-noise penalties, by incorporating sinusoidal z- and y- gradient wave perturbations into the EPI readout. Further acceleration capability will allow reduction of image distortion, achieving desired TE in high-res BOLD imaging, and temporal acceleration in SMS and 3D CAIPI EPI applications.Methods
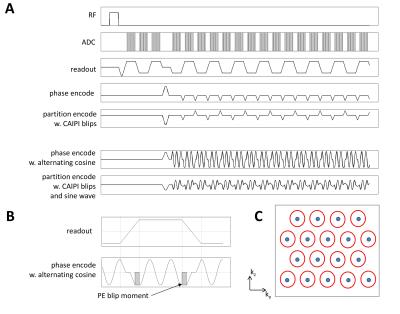
Wave-CAIPI EPI sequence: Three considerations complicate the implementation: (1) typical readout duration (echo spacing) is below 1ms (depending on spatial resolution and matrix size); this imposes significant time and slew-rate constraints on the waves (number of wave cycles, wave amplitude); (2) The alternating readout gradient requires a polarity reversal of the cosine wave (an even function) for alternate echoes; (3) The regular uni-directional EPI phase encoding blips must be accommodated, most economically into the ramp-up/ramp-down of the alternating cosine wave. The waves were incorporated into an in-house 3D CAIPI EPI sequence [8,13] shown in Figure 1.
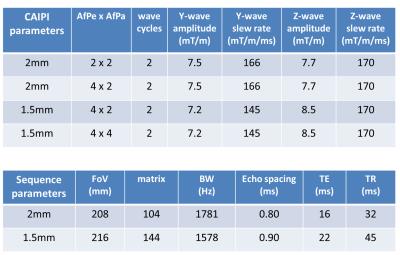
Data acquisition: Phantoms and N=3 human volunteers were scanned on a Siemens Magnetom 7T (32ch head coil, 70/200 body gradient). All imaging and CAIPI parameters are summarized in Figure 2.
Wave-CAIPI reconstruction: is extended to allow different point spread functions (psfs) for even and odd k-lines and to enable N/2 ghost correction. This will help address differences in corkscrew trajectory due to polarity reversal between alternating lines. The reconstruction then solves the system,
(see Fig 3)
where ρ is the unknown image, ke and ko are the acquired even and odd k-space lines, C are the coil sensitivities, G=ei(ax+b) is the 1st order ghost model and Fx is discrete Fourier transform along kx . Psfe and Psfo are the wave psfs for the odd and even lines, and Feyz and Foyz are undersampled Fourier transforms selecting the sampled even and odd lines in kx-ky.
Both the ghost term and even/odd psfs are estimated from the undersampled data without calibration measurement. This is achieved by a model reduction that summarizes the ghost model in 2, and psfs in 4 coefficients per y and z gradient axis, thus requiring estimation of only 10 numbers. These unknowns can then be simultaneously optimized with the parallel imaging reconstruction as per [14].
Results and Discussion
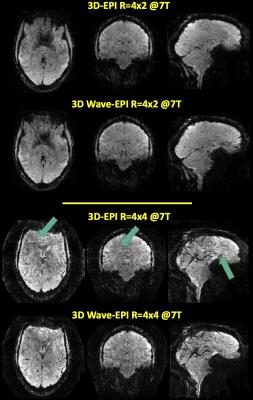
Successful wave-CAIPI
reconstructions were achieved for the 4x2 and 4x4 accelerated data, shown in
Figure 4. No CAIPI shift was used in this case. Improved reconstruction can be
noted in the 4x4 case, where in the central regions the wave sampling results
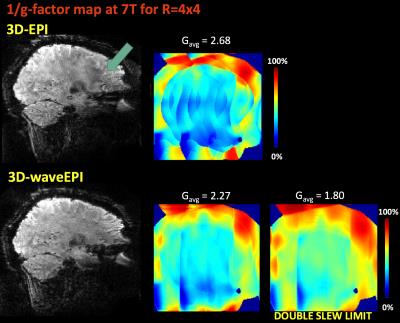
in lower residual artifact. This agrees with expectations, since the wave
gradients reduce the g-factor penalty by spreading the alias across the FoV
(Figure 5). Introducing CAIPI blips in addition to the waves will result
in further improvement.
As g-factor reduces with larger wave gradient moments, the application of stronger wave gradients will further improve the reconstruction. In particular, the use of head gradient systems will allow for a more significant sine/cosine perturbation during the short EPI readout (c.f. Fig 2).
wave-CAIPI EPI was here showcased for 3D EPI, but is directly applicable to 2D SMS EPI, owing to the direct 3D k-space analogy between the two [15,16]; SMS EPI will be explored next.
Conclusions
A wave-CAIPI EPI implementation was achieved at 7T, and initial in vivo data were successfully reconstructed. With further improvement in reconstruction the results hold promise that wave-CAIPI will bring further acceleration benefits even to EPI sequences, despite much tighter slew rate and amplitude constraints compared to e.g. GRE.Acknowledgements
Mahalo for the hospitality of our friends and colleagues at the University of Hawaii Neuroscience and MRI Research Program where this project was born.References
1. Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K; Wave-Caipi for Highly Accelerated 3D Imaging; Mag Res Med, 2015; 73(6):2152-2162
2. Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL, Setsompop K; RARE/Turbo Spin Echo Imaging with Simultaneous MultiSlice Wave-CAIPI; Mag Res Med, 2015; 73(3):929-38;
3. Polak D, Setsompop K, Cauley SF, Gagoski B.A, Bhat H, Maier F, Bachert P, Wald LL, Bilgic B; Wave-CAIPI for Highly Accelerated MP-RAGE Imaging; ISMRM 2017, submitted.
4. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med; 2005;53 (3):684–691.
5. Breuer F, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn. Reson. Med. 2006;55.3:549–556.
6. Breuer F, Moriguchi H, Seiberlich N, Blaimer M, Jakob PM, Duerk JL, Griswold MA. Zigzag sampling for improved parallel imaging. Magn. Reson. Med. 2008;60.2:474–478.
7. Feinberg DA, Moeller S, Smith SM, Auerbach EJ, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed Echo Planar Imaging for Sub-Second Whole Brain FMRI and Fast Diffusion Imaging. PLoS One. 2010; 5(12): e15710
8. Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuroimage 2010;51:261-6.
9. Setsompop K, Gagoski B, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced gfactor penalty. Magn. Reson. Med. 2012;67:1210–1224.
10. Setsompop, K., Cohen-Adad, J., Gagoski, B. A., Raij, T., Yendiki, A., Keil, B., Wedeen, V.J., Wald, L. L. (2012). Improving diffusion MRI using simultaneous multi-slice echo planar imaging. NeuroImage, 63(1), 569-580.10.1016/j.neuroimage.2012.06.033
11. Ivanov, D., Poser, B. A., Huber, L., Pfeuffer, J., & Uludag, K. (2016). Optimization of simultaneous multislice EPI for concurrent functional perfusion and BOLD signal measurements at 7T. Magn Reson Med. 10.1002/mrm.26351
12. Huber, L., Ivanov, D., Guidi, M., Turner, R., Uludag, K., Moller, H. E., & Poser, B. A. (2016). Functional cerebral blood volume mapping with simultaneous multi-slice acquisition. NeuroImage, 125, 1159-1168. doi: 10.1016/j.neuroimage.2015.10.082
13. Poser AB, Ivanov D, Kemper VG, Kannengiesser SA, Uludag K, Barth M. CAIPIRINHA-accelerated 3D EPI for high temporal and/or spatial resolution EPI acquisitions. ESMRMB congress, Toulouse, 2013
14. Cauley, S. F., Setsompop, K., Bilgic, B., Bhat, H., Gagoski, B., & Wald, L. L. Autocalibrated wave-CAIPI reconstruction; Joint optimization of k-space trajectory and parallel imaging reconstruction. Magn Reson Med. 2016; DOI: 10.1002/mrm.26499
15. Zahneisen, B., Ernst, T., & Poser, B. A. (2015). SENSE and simultaneous multislice imaging. Magn Reson Med, 74(5), 1356-1362.
16. Zahneisen, B., Poser, B. A., Ernst, T. E., & Stenger, V. A. (2013). Three-dimensional Fourier Encoding of Simultaneously Excited Slices: Generalized Acquisition and Reconstruction Framework. Magn Reson Med, Magn Reson Med. 2014 Jun;71(6):2071-81
Figures