1197
Trajectory Correction of Radial Data Using MUSSELS1Department of Radiology, University of Iowa, Iowa City, IA, United States, 2Department of Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States
Synopsis
Radial acquisitions are time efficient and flexible and enable several MR imaging applications. However, the sensitivity of radial acquisitions to trajectory deviations can result in severe artifacts in the images. We propose a trajectory correction method that can reconstruct the images for the ideal trajectory without the need for trajectory estimation or calibration.
Introduction
Non-Cartesian trajectories are often more efficient in terms of k-space sampling and can offer desirable imaging properties compared to conventional Cartesian trajectories for various applications. For example, radial sequences are emerging as the trajectory of choice for high temporal and spatial resolution cardiac imaging because of their simplicity, ability to do 2-D under-sampling and its robustness to under-sampling. A challenge with radial sequences is the trajectory errors, resulting from gradient delays, eddy currents, and non-ideal gradient amplifier characteristics1. If uncorrected, these errors can cause severe image distortions. Existing methods that correct for the trajectory errors require specialized sequences or field monitoring probes to measure the trajectory2,3. The purpose of this work is to generalize our previous work termed as MUSSELS4,5, originally designed for trajectory correction in echo-planar imaging (EPI), to radial sequences. The main benefit of this scheme is that it does not require specialized navigators or trajectory measurement sequences to aid the reconstruction.Methods
The gradient timing imperfections and eddy currents in EPI cause the phase-encoding lines of opposite polarity to be shifted from each other, resulting in Nyquist-ghost artifacts. MUSSELS is based on the idea that phase inconsistencies between two images can be captured by a small annihilating FIR filter in the Fourier domain. These annihilation relations translate to null space conditions of a block-Hankel matrix, whose entries are the k-space data from the odd/even lines. Since these null-space conditions imply that the block Hankel matrix is low-rank, we used structured low-rank matrix completion to fill in the missing lines in each set.
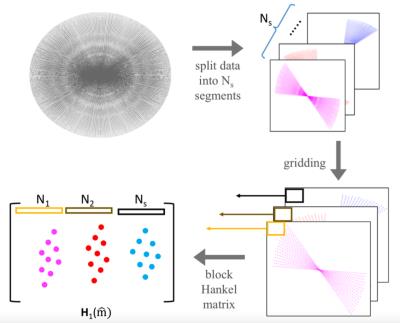
Here, we generalize the EPI correction scheme to radial trajectories. In particular, we assume that radial spokes with similar angles (small angular difference) experience the same phase error. We split the k-space data of a given frame with $$$N$$$ spokes, denoted by $$$\bf{ y}$$$, into $$$N_s$$$ segments: $$$\mathbf y_i, i=1:N_s$$$. We denote the images on the Cartesian lattice, corresponding to these segments as $$$\mathbf m_i; i=1,..,N_s$$$ and they satisfy $$$\mathcal A_i(\mathbf m_i)=\mathbf y_i + \mathbf n_i$$$, where $$$\mathbf n_i$$$ is the noise and $$$\mathcal A$$$ is the forward model; it consists of multichannel sensitivity weighting and non-uniform Fourier transform to the trajectory corresponding to the $$$i^{\rm th}$$$ segment. We construct a block-Hankel matrix:\begin{equation}{\bf{{H}}(\hat{m})}=\begin{bmatrix} {\bf{\cal H}}(\widehat{{\bf{m}}_1}) & {\bf{\cal H}}(\widehat{{\bf{m}}_2}) & ... & {\bf{\cal H}}(\widehat{{\bf{m}}_{N_s}}) \end{bmatrix},\end{equation}where $$$\mathcal H(\widehat{{\bf{m}}_i})$$$ denotes the block-Hankel matrix, whose entries are the uniform Fourier samples of $$$\mathbf m_i$$$. The structure of the Hankel matrix implies that the multiplication $$$\mathcal H(\widehat{{\bf{m}}_i}) \mathbf v$$$ is equivalent to the convolution of the Fourier samples $$$\widehat{\mathbf m_i}$$$ by the 2D FIR filter $$$v$$$. As discussed earlier, the phase relations between the segments implies that $$${\bf{{H}}(\hat{m})}$$$ is low-rank. We propose to recover the images $$$\mathbf m_i; i=1,..,N_s$$$ by solving the following problem: \begin{equation}\{\tilde {\mathbf m_i},i=1,..,N_s\}= \text{argmin}_{\{ {\mathbf m_i},i=1,..,N_s\}} \left(\sum_{i=1}^{N_s}~\|\mathcal{A}_i(\mathbf m_i)-\mathbf y_i\|^2_{\ell_2} + \lambda||{\bf{{H}}_1(\hat{m})}||_*\right) . \end{equation}The above nuclear norm minimization problem can be solved using an ADMM algorithm.
Radial data acquired on a phantom and a healthy volunteer are used for validation of the proposed method. The imaging parameters for the phantom data were: FOV=300mmx300mm, matrix size=256x154 partial Fourier acquisition using a fast gradient-echo sequence. The cardiac data was acquired using a SSFP sequence on a 3T Siemens TIM Trio scanner using a uniform radial trajectory in the breath-held mode. The scan parameters were: TR/TE=3.4/1.72ms, FOV=300mmx300mm, matrix size=512x512 number of cardiac phases=18, radial views/cardiac phase=253 and 16s of breath-hold.
Results
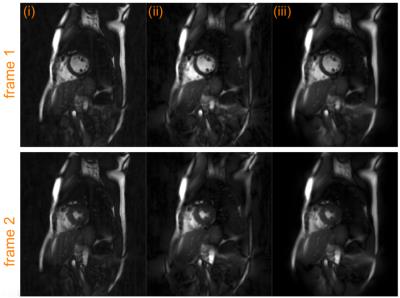
Figure 2 shows the results from the phantom data. The data was reconstructed using three methods: (i) the k-space trajectory was rounded to Cartesian coordinates and the data gridded to the Cartesian co-ordinates were reconstructed using Fourier transforms, (ii) using an iterative SENSE method using non-uniform fast Fourier transforms (CG-NUFFT) and (iii) using the proposed MUSSELS method. Artifacts arising from the trajectory errors are clearly visible in the CG-NUFFT results while the gridded data is dominated by errors from the trajectory approximation. The proposed method split the data into 4 segments and recovered the trajectory corrected k-space data using the formulation proposed above, giving improved reconstruction results compared to the other methods. Figure 3 shows the reconstruction results of in-vivo cardiac data. Here also, the gridded reconstruction and the CG-NUFFT reconstruction results show artifacts. Using the proposed method, we split the data into 11 segments and recovered the trajectory corrected reconstruction. The resulting images show much less artifacts compared to other reconstruction.Conclusion
We proposed a simple trajectory correction method for radial data that does not require trajectory estimation or specialized acquisition. The method is shown to work well on phantom and in-vivo data.Acknowledgements
No acknowledgement found.References
1. Addy, N. O., Wu, H. H., & Nishimura, D. G. (2012). A Simple Method for MR Gradient System Characterization and k-Space Trajectory Estimation. Magnetic Resonance in Medicine, 68(1), 120–129. http://doi.org/10.1002/mrm.23217
2. Zhang Y, Hetherington HP, Stokely EM, Mason GF, Twieg DB. A novel k-space trajectory measurement technique. Magn Reson Med 1998;39:999–1004.
3. Mason GF, Harshbarger T, Hetherington HP, Zhang Y, Pohost GM,Twieg DB. A method to measure arbitrary k-space trajectories for rapid MR imaging. Magn Reson Med 1997;38:492–496.Mani,
4. M., Jacob, M., Kelley, D. and Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. doi: 10.1002/mrm.26382, 2016
5.Mani, M., Jacob, M., Kelley, D. and Magnotta, V. (2016), Comprehensive Reconstruction of Multi-shot Multi-channel Diffusion Data Using MUSSELS. Conf Proc IEEE Eng Med Biol Soc. 2016, Orlando, Fl Aug 16-20, 2016.
Figures