1167

Accelerated parameter mapping with compressed sensing: an alternative to MR Fingerprinting

Pedro A. Gómez^1,2, Guido Buonincontri³, Miguel Molina-Romero^1,2, Jonathan I. Sperl², Marion I. Menzel², and Bjoern H. Menze¹

¹Technical University of Munich, Munich, Germany, ²GE Global Research, Munich, Germany, ³Imago7 Foundation, Pisa, Italy

Synopsis

We introduce a method for MR parameter mapping based on three concepts: 1) an inversion recovery, variable flip angle acquisition strategy designed for speed, signal, and contrast; 2) a compressed sensing reconstruction which exploits spatiotemporal correlations through low rank regularization; and 3) a model-based optimization to simultaneously estimate proton density, T1, and T2 values from the acquired measurements. Compared to MR Fingerprinting, the proposed method achieves a five-fold acceleration in acquisition time, reconstructs an unaliased series of images, and does not rely on dictionary matching for parameter estimation.

Purpose

MR Fingerprinting (MRF)[1] has recently gained attention due to its ability to simultaneously estimate multiple parametric maps within clinically feasible scan times. MRF is based on three main ingredients: a pseudorandom acquisition, the reconstruction of aliased measurements, and the matching of these measurements to a precomputed dictionary. While conceptually appealing, MRF suffers from multiple methodological shortcomings. The purpose of this work is to present an alternative method to parameter mapping that addresses these limitations by optimizing the acquisition, reconstructing unaliased measurements, and fitting the measurements in a model-based optimization not subject to the discretization of the dictionary.

Methods

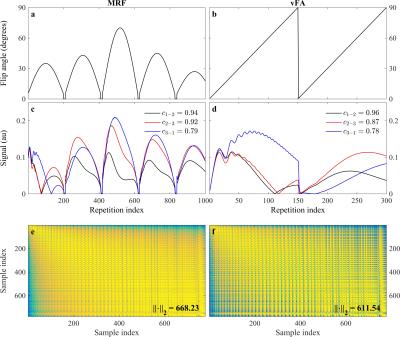
In an MRI experiment the observed signal $$$y(t)$$$ can be described by the combination of a spatial function with a temporal signal evolution: $$y(t)=\int_{\mathbf{r}}\rho(\mathbf{r})f_t(\mathbf{r})e^{2\pi i\mathbf{k}(t)\cdot\mathbf{r}}d\mathbf{r}$$ where $$$\rho (\mathbf{r})$$$ is the spatial distribution of the spin density at position $$$\mathbf{r}$$$, $$$\mathbf{k}(t)$$$ is the k-space trajectory, and $$$f_t(\mathbf{r})$$$ is the temporal signal, given by the recursion: $$f_t(\mathbf{r})=f_{t-1}(\mathbf{r})g\left( \boldsymbol{\theta}_a(t);\boldsymbol{\theta}_b(\mathbf{r})\right). $$ The temporal signal $$$f_t(\mathbf{r})$$$ at time $$$t$$$ is determined by the signal value at the previous time point modulated by $$$g\left( \cdot \right)$$$, a function of two different parameter sets: the temporally varying acquisition parameters $$$\boldsymbol{\theta}_a(t)$$$, e.g. flip angle $$$\alpha (t)$$$ and repetition time $$$T_R(t)$$$; and the spatially dependent biological parameters of interest $$$\boldsymbol{\theta}_b(\mathbf{r})$$$, such as $$$T_1(\mathbf{r})$$$ and $$$T_2(\mathbf{r})$$$. In MRF, the temporal signals are denoted fingerprints, where the method aims at creating unique signals for different spatial locations through pseudorandom variations of the acquisition parameters $$$\boldsymbol{\theta}_a(t)$$$. Alternatively, we chose $$$\boldsymbol{\theta}_a(t)$$$ to satisfy three criteria: speed, signal, and contrast. We increased the speed by minimizing $$$T_R(t)$$$, and optimized $$$\alpha(t)$$$ for signal and contrast using a training dataset $$$\mathbf{x} \in \mathbb{C}^{L\times T}$$$ with $$$L$$$ observations and $$$T$$$ time points; wherein we experimentally attempted to increase both the orthogonality between observations, and the norm within observations[2]–[4].

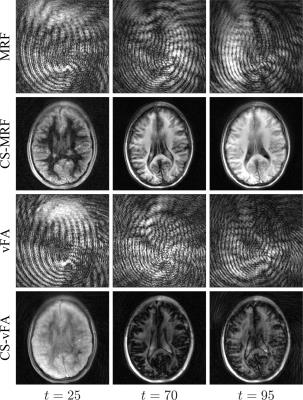
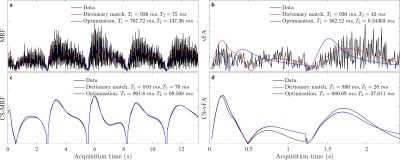
Whereas the original MRF reconstructs aliased images from the measurements, recent work has shown that the acquired data can also be reconstructed in an iterative framework[5]–[10]. Based on these ideas, we implemented a compressed sensing (CS)[11] reconstruction that constrains the temporal signal evolution to a low dimensional subspace[6],[9], and regularizes the image series by promoting local low rank of spatiotemporal image patches[12],[13]. Finally, once we reconstruct an unaliased image series, we propose to replace the matching to a simulated dictionary with an optimization based on least-squares curve fitting for the simultaneous estimation of $$$\rho (\mathbf{r})$$$, $$$T_1(\mathbf{r})$$$ and $$$T_2(\mathbf{r})$$$.

We acquired a single slice from a healthy volunteer based on the FISP implementation of MRF[14] on a GE HDx MRI system (GE Medical Systems, Milwaukee, WI), with an eight channel receive only head RF coil. After an initial inversion, we applied a train of $$$T=1000$$$ pulses with $$$\alpha(t)$$$ and $$$T_R(t)$$$ as in[14] ($$$T_{acq}=12.67\ s$$$ per slice). In addition, we acquired a train of $$$T=300$$$ variable flip angles (vFA) (Fig. 1b) with $$$T_R=8 \ ms$$$ ($$$T_{acq} = 2.42 \ s$$$ per slice). For both acquisitions, we used a variable density spiral designed with $$$22.5\times 22.5\ cm^{2}$$$ FOV, $$$256\times 256$$$ matrix size, $$$1 \ mm$$$ in-plane resolution, $$$5\ mm$$$ slice thickness, and golden angle rotations between every interleave. Each acquisition was reconstructed using the nuFFT operator[15] and with the proposed CS method, and parameter maps were subsequently estimated with both dictionary matching and optimization. We simulated the dictionary using the EPG formalism[16], [17].

Results

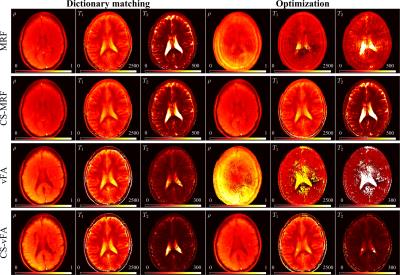
We found that a vFA scheme of two linear ramps yielded $$$T_1$$$ and $$$T_2$$$ sensitivity while reducing the cost (see Fig. 1). Compared to MRF, the proposed strategy reduces the number of repetitions (Fig. 1a-b), while increasing the orthogonality of the signal evolutions between training observations (Fig. 1c-d). This acquisition, coupled with the proposed CS reconstruction, allows for the recovery of a series of unaliased images (Fig. 2), which in turn facilitate a model-based optimization for parameter mapping (Figs. 3,4).

Discussion

When the measurements are aliased, the optimization is subject to local minima due to high noise levels of the temporal signals, resulting in biased parameter estimates. On the other hand, as soon as the image series is unaliased, the optimization converges, yielding parametric maps that are not subject to the discretization of the dictionary. vFA maps display an underestimation of $$$T_2$$$ values, indicating that the vFA strategy could still benefit from higher sensitivity $$$T_2$$$ encoding.

Conclusion

We demonstrated an alternative to MRF based on variable flip angles, a compressed sensing reconstruction, and a model-based optimization. Our proposal reduces the acquisition time by a factor of five, reconstructs unaliased temporal signals, and, notably, does not rely on dictionary matching for parameter estimation.

Acknowledgements

With the support of the TUM Institute for Advanced Study, funded by the German Excellence Initiative and the European Commission under Grant Agreement Number 605162.

References

[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, pp. 187–192, 2013.

[2] O. Cohen, “Magnetic Resonance Fingerprinting Trajectory Optimization,” Proc Intl Soc Mag Reson Med, vol. 1, p. 1, 2014.

[3] O. Cohen, M. Sarracanie, M. S. Rosen, and J. L. Ackerman, “In Vivo Optimized Fast MR Fingerprinting in the Human Brain,” Proc Intl Soc Mag Reson Med, 2016.

[4] J. I. Hamilton, K. L. Wright, Y. Jiang, L. Hernandez-Garcia, D. Ma, M. Griswold, and N. Seiberlich, “Pulse Sequence Optimization for Improved MRF Scan Efficiency,” Proc Intl Soc Mag Reson Med, vol. 23, p. 3386, 2015.

[5] E. Y. Pierre, D. Ma, Y. Chen, C. Badve, and M. A. Griswold, “Multiscale reconstruction for MR fingerprinting,” Magn. Reson. Med., vol. 2492, pp. 2481–2492, 2015.

[6] B. Zhao, F. Lam, B. Bilgic, H. Ye, and K. Setsompop, “Maximum likelihood reconstruction for magnetic resonance fingerprinting,” in 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, vol. 1, pp. 905–909.

[7] B. Zhao, K. Setsompop, B. Gagoski, H. Ye, E. Adalsteinsson, P. E. Grant, and L. L. Wald, “A Model-Based Approach to Accelerated Magnetic Resonance Fingerprinting Time Series Reconstruction,” Proc Intl Soc Mag Reson Med, 2016.

[8] P. A. Gómez, C. Ulas, J. I. Sperl, T. Sprenger, M. Molina-Romero, M. I. Menzel, and B. H. Menze, “Learning a spatiotemporal dictionary for magnetic resonance fingerprinting with compressed sensing,” MICCAI Patch-MI Work., vol. 9467, pp. 112–119, 2015.

[9] C. C. Cline, X. Chen, B. Mailhe, Q. Wang, and M. Nadar, “AIR-MRF: Accelerated iterative reconstruction for magnetic resonance fingerprinting,” Proc Intl Soc Mag Reson Med, 2016.

[10] J. Assländer, M. A. Cloos, F. Knoll, D. K. Sodickson, J. Hennig, and R. Lattanzi, “Low Rank Alternating Direction Method of Multipliers Reconstruction for MR Fingerprinting,” arXiv eprint, p. arXiv:1608.06974, 2016.

[11] M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging.,” Soc. Magn. Reson. Med., vol. 58, pp. 1182–1195, 2007.

[12] J. I. Tamir, M. Uecker, W. Chen, P. Lai, M. T. Alley, S. S. Vasanawala, and M. Lustig, “T 2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging,” Magn. Reson. Med., 2016.

[13] J. Trzasko and A. Manduca, “Local versus Global Low-Rank Promotion in Dynamic MRI Series Reconstruction,” Proc Intl Soc Mag Reson Med, vol. 24, no. 7, p. 4371, 2011.

[14] Y. Jiang, D. Ma, N. Seiberlich, V. Gulani, and M. A. Griswold, “MR Fingerprinting Using Fast Imaging with Steady State Precession (FISP) with Spiral Readout,” MRM, 2014.

[15] J. A. Fessler and B. P. Sutton, “Nonuniform Fast Fourier Transforms Using Min-Max Interpolation,” IEEE Trans Signal Process., vol. 51, no. 2, pp. 560–574, 2003.

[16] J. Hennig, “Echoes—how to generate, recognize, use or avoid them in MR-imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes,” Concepts Magn. Reson., vol. 3, no. 3, pp. 125–143, Jul. 1991.

[17] M. Weigel, “Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple,” J. Magn. Reson. Imaging, 2014.

Figures

Figure 1: Flip angle trajectories and correlation between observations. a-b, Flip angle trajectory for MRF and variable flip angles (vFA). c-d, Temporal signal evolution of three exemplary observations. The legend displays the correlation $$$c$$$ between each of them. e-f, Correlation matrix for all observations and the norm of the matrix; where the observations are less correlated in vFA.

Figure 2: Reconstructed images at different repetition indexes $$$t$$$. While the nuFFT operation reconstructs a series of aliased images, the proposed CS reconstruction removes the aliasing, allowing for an easier visualization of the temporal dynamics of the signal.

Figure 3: Signal evolution of a single observation with dictionary matching and model-based optimization. a-b, The high levels of aliasing in the acquisitions lead to different parameter estimates between matching and optimization. c-d, Matching and optimization results are similar when the evolution is unaliased, where the optimization is not constrained to the discretization of the dictionary. The $$$T_2$$$ values obtained from CS-vFA present an underestimation with respect to the $$$T_2$$$ in MRF and CS-MRF.

Figure 4: Estimated parametric maps with dictionary matching and model-based optimization. Dictionary matching yields consistent results with noisy and unaliased signals, while the optimization only converges when fitting unaliased signals (rows 2 and 4, right). When fitting noisy signals, the optimization converges to local minima, leading to an incorrect estimation of parametric maps (rows 1 and 3, right). On the other hand, the optimization is not subject to dictionary discretization, allowing for a wider range of parameters in the solution space. $$$T_2$$$ maps in vFA are underestimated in comparison to MRF.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1167