1139
Inversion Parameters based on Convergence and Error Metrics for Nonlinear Inversion MR ElastographyAaron T Anderson1,2, Curtis L Johnson3, Matthew DJ McGarry4,5, Keith D Paulsen4,6, Bradley P Sutton2,7, Elijah EW Van Houten4,8, and John G Georgiadis9
1Mechanical Science & Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Biomedical Engineering, University of Delaware, Newark, DE, United States, 4Thayer School of Engineering, Dartmouth College, Hanover, NH, United States, 5Biomedical Engineering, Columbia University, New York, NY, United States, 6Radiology, Dartmouth-Hitchcock Medical Center, Lebanon, NH, United States, 7Bioengineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 8Génie Mécanique, Université de Sherbrooke, Sherbrooke, QC, Canada, 9Biomedical Engineering, Illinois Institute of Technology, Chicago, IL, United States
Synopsis
Nonlinear inversion (NLI) of brain MRE data has shown the promise in sensitive detection of complex neurodegenerative disease by showing repeatable and accurate assessments of both white matter and gray matter regions in healthy subjects. This study looks to further improve the accuracy of the NLI-MRE framework by characterizing two major inversion parameters: subzone size and conjugate gradient iterations. Additionally, two convergence criteria are proposed as means to quantify the confidence in final reported statistics while fully capturing the distribution of heterogeneity within white matter regions.
Introduction
Magnetic resonance elastography (MRE) has shown promise in resolving local mechanical properties related to the microstructure of the human brain.1-3 The nonlinear inversion (NLI) algorithm provides an avenue for more accurate and reliable property maps through its inhomogeneous finite-element formulation.4-6 In order for NLI-MRE to provide patient-specific estimates, it is necessary to accurately reconstruct viscoelastic material properties in relatively small heterogeneous regions in the brain.4 To reduce computational burden,1 NLI decomposes the entire domain into a set of overlapping smaller regions of a specified size (subzones), where an iterative conjugate gradient (CG) optimization process updates an estimate of the mechanical properties. The subzone solutions are collected, smoothed, and the subzone process is repeated with new randomly generated subzones until the property estimate converges. This study aims to characterize the effect of two major inversion parameters – subzone size and CG iterations – on the reconstruction of local mechanical properties. The parameters are chosen based on independent measurements with dynamic mechanical analysis (DMA) in phantoms and convergence criteria in a human subject.Methods
One healthy subject underwent eight repeated MRE experiments, with diffusion tensor imaging (DTI) and high-resolution T1-weighted anatomical imaging for registration1,8 acquired in tandem. A Resoundant pneumatic driving system applied 50 Hz vibrations to the head to generate shear waves; MRE phase imaging captured the complex displacement field;7 and NLI estimated the material property maps.4,5 Imaging was performed on a Siemens 3T Trio scanner with 32-channel head coil. MRE imaging parameters included: two-shot in-plane spiral readout with SENSE (R = 2); ten slabs of eight sampling planes with 25% slab overlap; TR/TE = 1800/73 ms; four (4) temporal phase offsets; and FOV = 240x240x120 mm with 2x2x2 mm3 isotropic spatial resolution.1 All experimental conditions were consistent between datasets, leaving scanner each time. We processed displacement datasets using NLI with a range from 1 to 5 CG iterations and subzone sizes based on expected shear wavelength, $$$L_s = \frac{1}{f} \sqrt{G’/\rho}$$$. We prescribed cubic subzones with edge lengths of $$$L_s/4$$$, $$$L_s/2$$$, $$$0.64L_s$$$, $$$3L_s/4$$$, and $$$L_s$$$. The reference shear wavelength for the phantom is $$$23.5 ~\mathrm{mm}$$$ and $$$30.6~\mathrm{mm}$$$ for the human brain. The $$$0.64L_s$$$ subzone is included as the "standard" size, which, along with CG=2, was chosen based on the experience of stability and convergence in numerical, phantom, and in vivo studies described in previous works.1-3,5-7Results and Discussion
The size of the subzones and the CG
iterations are two of the most dominant parameters affecting the reconstruction
of the viscoelastic shear modulus (G = G' + i G''); see Figures 1 and 2.
Figure 1, and the accompanying statistics for an inclusion (large bottom-right)
in Figure 3, show an optimal subzone size near $$$3L_s/4$$$ and increasing CG
iterations improves the estimate towards the DMA results. The much softer
surrounding silicone appears to affect the NLI material reconstruction. Figure
2 shows results from this subzone size have pronounced rigidity in the region
of the falx cerebri, known to be stiff compared to healthy brain tissue, but
only for the largest subzone ($$$L_s$$$).
Figure 4 shows a proposed convergence
criteria defined relative to the variation of properties with last ten global
iteration in NLI: variation relative to mean (“percent”) and variation relative
to [Pa] threshold (“constant”). The convergence criteria highlight the
stability of the reconstructed values on a voxel-wise basis. Specifically, we
report the percent of voxels in the region mask that are converged according to
the specific criteria. Figure 5 shows the effect of the convergence criteria on
the reported statistics (average and standard deviation) for the superior
longitudinal fasciculus (SLF) white matter region. The statistics for each
convergence criteria are nearly identical and unchanged above 300 global
iterations, but decreasing the threshold
level improves the confidence in the
final statistics.Conclusions
Choosing the optimal MRE-NLI parameters is a balance between the subzone containing sufficient spatial resolution to capture complex internal property features while not allowing regions not appropriately modeled, like the falx, to corrupt surrounding tissue estimates. In the phantom, the NLI reconstructions matched the expected contrast but did not exactly match the DMA results; however, increasing the number of CG iterations improved the estimate and was likely affected by the surrounding soft background. The proposed convergence criteria show the capability of capturing the full statistics of an important white matter region while improving the confidence in the final reported statistics. This allows NLI-MRE to be tailored to the material or tissue under investigation by choosing the subzone based on expected bulk properties and a priori convergence criteria can ensure accurate estimations.Acknowledgements
Support for ATA and JGG was provided by NSF Grant CMMI-1437113. Partial support was provided by the Biomedical Imaging Center of the Beckman Institute for Advanced Science and Technology at the University of Illinois at Urbana-Champaign (UIUC), NIH Grant R01-EB018230, and NIH/NIBIB Grant R01-EB001981. This research is part of the Blue Waters sustained-petascale computing project, which is supported by the National Science Foundation (awards OCI-0725070 and ACI-1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana-Champaign and its National Center for Supercomputing Applications.References
[1] CL Johnson, et al., Local mechanical properties of white matter structures in the human brain, Magn Reson Med, 2013, 70(2):404-412; [2] CL Johnson, MDJ McGarry, et al., Medial temporal lobe viscoelasticity and relational memory performance. NeuroImage, 2016, 132, 534-541; [3] CL Johnson, et al., Viscoelasticity of subcortical gray matter structures. Hum. Brain Mapp, 2016, 37(12):4221-4233; [4] Van Houten EEW, et al. An overlapping subzone technique for MR-based elastic property reconstruction. Magn Reson Med, 1999, 42(4):779-786; [5] McGarry MDJ, et al. Multiresolution MR elastography using nonlinear inversion. Med Phys, 2012, 39(10):6388-6396; [6] McGarry MDJ, et al. Spatially-Resolved Hydraulic Conductivity Estimation Via Poroelastic Magnetic Resonance Elastography. IEEE T Med Imaging, 2013, 32(10):1901-1909; [7] CL Johnson, et al. 3D multislab, multishot acquisition for fast, whole-brain MR elastography with high signal-to-noise efficiency. Magn Reson Med, 2014; 71(2):477-485; [8] Mori et al., MRI Atlas of Human WM, 2005;Figures
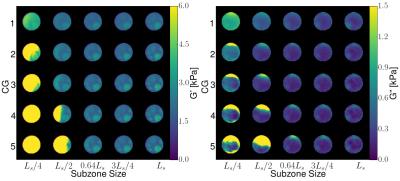
Figure 1: NLI reconstructed material properties for a
phantom constructed using silicone A341 with five inclusions over a range of
concentrations (50-70%) and background concentration of 50%. Qualitatively, the
contrast is improved around $$$3L_s/4$$$ subzone size and with increasing CG
iterations.
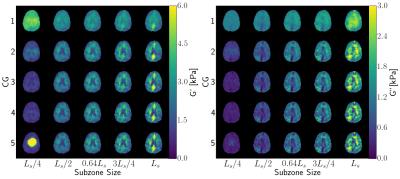
Figure 2: NLI reconstructed material properties for the
human subject over thr range of NLI parameters shows the best contrast and
sharpness for subzone sizes around $$$0.64L_s$$$ and $$$3L_s/4$$$. There are
significant issues for small ($$$L_s/4$$$) and large ($$$L_s$$$) subzones. Qualitatively,
increasing the CG iterations improves contrast for nearly all cases.
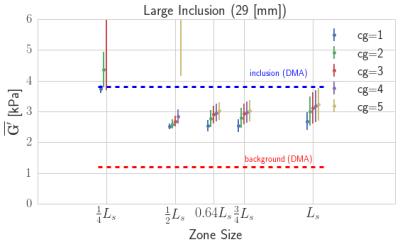
Figure 3: The average and standard deviations, across NLI
parameters, of one inclusion in the silicone phantom (large, bottom-right in
Figure 1) are shown with DMA results for the inclusion and background. Subzone
sizes near $$$3L_s/4$$$ are the closest to DMA results and increasing CG
iterations improves the estimate. The softer background seems to have an effect
on the stiffer inclusion estimations.
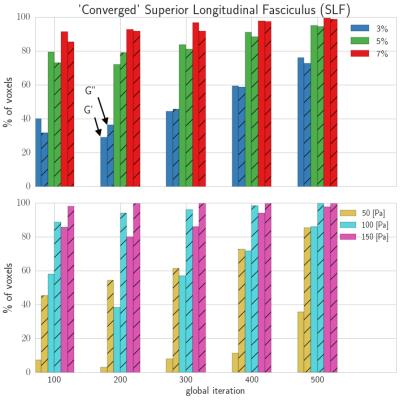
Figure 4: Two convergence criteria are proposed: percent
variation and absolute variation in property estimates across last ten NLI global
iterations. The percent of total voxels “converged” within the SLF are reported
(G’ – solid; G’’ – hashed) for a set of global iterations. Global iteration
always improves convergence, and 3% and 100 [Pa] convergence thresholds are
reasonably discerning without being overly restrictive.
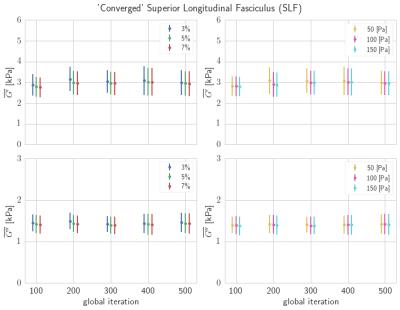
Figure 5: In the SLF, the average and standard deviation,
based on the two types of convergence criteria, are compared across global
iterations. For all convergence criteria, the statistics are nearly unchanged
for NLI global iterations above 300. The choice of convergence criteria is then
chosen based on the desired level of confidence in the final statistics.