1137
Quadrature Motion Encoding (QuME): A Novel Motion Encoding Scheme for MR Elastography1Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
We propose a novel approach to motion encoding for spin-echo-based MR elastography called quadrature motion encoding (QuME) in which the second
Introduction
MR elastography (MRE) is an emerging imaging technique that quantitatively measures the stiffness of soft tissues (e.g., liver, brain, and heart) from images of shear wave propagation in the tissue1-4. In a typical MRE acquisition, the shear wave is encoded into the phase of the MR signal by additional motion-encoding gradients (MEGs) that are present during the tissue vibration, and 3–8 phase offsets between the motion and MEGs are acquired to temporally sample one motion period. Such phase offsets often can be introduced by a variable delay between the start of the motion and the MEG. This may cause a motion discontinuity when transitioning between phase offsets and require additional discarded acquisitions to ensure the motion has returned to a steady state, leading to an increased scan time. Moreover, the delay method may constrain the efficiency of certain advanced MRE encoding schemes. For example, in SLIM-MRE, where the scan time can be accelerated by encoding three components of motion simultaneously, the echo time typically has to be increased by 25% of the motion period at a minimum due to its particular MEG-shifting scheme, resulting in a SNR loss5. Here we propose a new approach to motion encoding for spin-echo sequences called quadrature motion encoding (QuME), in which the second MEG after the refocusing pulse is used to record the quadrature phase of the harmonic motion. Unlike the conventional encoding method that shifts the temporal relation between the motion and MEGs, QuME alters the amplitudes of MEGs from one time step to the next. This technique was implemented on a 3T GE scanner to demonstrate its ability to shorten the echo time of SLIM-MRE for human brain.Theory
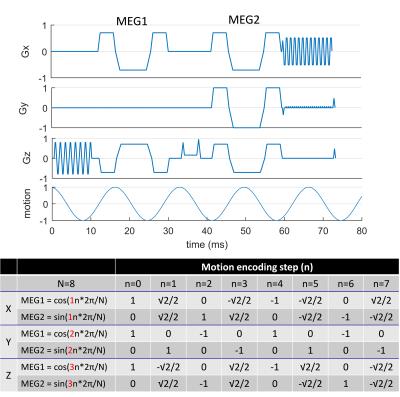
The accumulated phase of an MR image φ at the nth motion-encoding step can be written as Eq.(1). Recombining the phase offset term with G(t) gives Eq.(2), indicating that we can separate two MEGs by an odd integer multiple of 1/4 motion period to be sensitive to the in-phase and the quadrature components of the motion. Different phase offsets can be achieved solely by modulating the two MEG amplitudes using Eq.(3). See Figure 1 for details.Method
Human volunteer scans were conducted on a GE 3T scanner with an 8-channel head coil and a soft pillow-like head driver. The QuME scheme was implemented into a spin-echo EPI MRE sequence, and a SLIM scheme was used for demonstration. Unlike the conventional SLIM-MRE technique that changes the MEG locations and polarities to obtain different phase offsets5,6, QuME achieved multiple phase offsets by varying the MEG amplitudes without moving them in time, leading to a shorter echo time. As illustrated in Fig.2, MEGs in QuME are moment nulled with amplitudes specified by Eq. (3) varying at each phase offset (N=8). Both conventional and QuME methods were performed with: 60-Hz mechanical motion, TR=3000 ms, TE=86 ms (conv.) vs. 65.1 ms (QuME), FOV=24x24cm2, slice thickness=3mm, and acquisition matrix=72x72. For each motion-encoding step, two acquisitions with opposite MEG polarities were used for phase-difference calculation to remove the background phase and double the motion sensitivity. To match the encoding efficiency, the maximum MEG amplitudes were 40 mT/m and 20 mT/m for QuME and conventional encoding, respectively. The shear wave images were calculated from the harmonic components of the Fourier transform of the 8 time steps. The stiffness maps were then calculated by a direct inversion algorithm described elsewhere7.Results
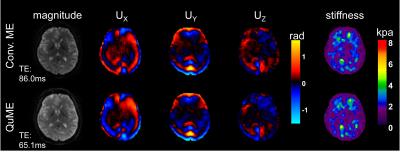
Figure 3 shows the magnitude images, the shear wave images of three directional components, and the stiffness maps comparing conventional motion encoding and QuME. The overall magnitude SNR using QuME is 33% higher due to the shorter TE.Discussion
Our preliminary results demonstrated the feasibility of the QuME scheme and showed its ability to decrease the TE for the SLIM-MRE by removing the time-shifting aspect of the technique. Compared with another recent MRE study using MEGs with varying initial phases to avoid the temporal shifting8, the QuME method does not change the MEGs’ moment nulling characteristics between encoding steps, making it immune to the phase errors that arise from the involuntary movement of human subjects. Though the encoding efficiency of QuME is 50% of the conventional encoding technique for the same maximum MEG strength, the SNR gain due to the shorter TE can be very helpful in situations where T2 is critically short (e.g., liver with iron overload).Conclusion
We proposed a novel quadrature motion-encoding scheme for MRE that modulates MEG amplitudes instead of shifting the motion and the MEGs in time and we demonstrated its ability to reduce the echo time of SLIM-MRE.Acknowledgements
No acknowledgement found.References
1. Muthupillai, R. & Ehman, R. L. Magnetic resonance elastography. Nat Med 2, 601-603, (1996).
2. Mariappan, Y. K., Glaser, K. J. & Ehman, R. L. Magnetic resonance elastography: a review. Clin Anat 23, 497-511, (2010).
3. Venkatesh, S. K., Yin, M. & Ehman, R. L. Magnetic resonance elastography of liver: technique, analysis, and clinical applications. J Magn Reson Imaging 37, 544-555, (2013).
4. Arani, A., Glaser, K. L., Arunachalam, S. P., Rossman, P. J., Lake, D. S., Trzasko, J. D., Manduca, A., McGee, K. P., Ehman, R. L. & Araoz, P. A. In vivo, high-frequency three-dimensional cardiac MR elastography: Feasibility in normal volunteers. Magn Reson Med, (2016).
5. Klatt, D., Johnson, C. L. & Magin, R. L. Simultaneous, multidirectional acquisition of displacement fields in magnetic resonance elastography of the in vivo human brain. J Magn Reson Imaging 42, 297-304, (2015).
6. Klatt, D., Yasar, T. K., Royston, T. J. & Magin, R. L. Sample interval modulation for the simultaneous acquisition of displacement vector data in magnetic resonance elastography: theory and application. Phys Med Biol 58, 8663-8675, (2013).
7. Manduca, A., Oliphant, T. E., Dresner, M. A., Mahowald, J. L., Kruse, S. A., Amromin, E., Felmlee, J. P., Greenleaf, J. F. & Ehman, R. L. Magnetic resonance elastography: non-invasive mapping of tissue elasticity. Med Image Anal 5, 237-254, (2001).
8. Kearney, S. P., Brinker, S. T., Burns1, D. A., Royston, T. J. & Klatt, D. SLIM-MRE without prolonged echo time for the simultaneous acquisition of the 3D displacement vector applied to in vivo mouse brain. ISMRM, (2016).
Figures