1136
Measurement of Human Brain, Scalp, and Skull Motion in vivo using Magnetic Resonance Elastography and Triaxial AccelerometersAndrew A Badachhape1, Ruth J Okamoto2, Curtis L Johnson3, and Philip V Bayly1,2
1Biomedical Engineering, Washington University in St. Louis, St. Louis, MO, United States, 2Mechanical Engineering and Materials Science, Washington University in St. Louis, St. Louis, MO, United States, 3Biomedical Engineering, University of Delaware, Newark, DE, United States
Synopsis
Characterizing motion transmission from the skull to the brain and from skull to external soft tissue would provide valuable insight into traumatic brain injury mechanics and injury assessment by external sensors. In this study, we estimated rigid-body displacement components of brain and scalp using magnetic resonance elastography for comparison with skull motion estimated from three triaxial accelerometers. Comparison of the relative amplitudes and phases of harmonic motion in the skull, scalp, and brain of five human subjects indicated differences between each region. These measured amplitude and phase relationships can improve both simulations and experimental characterization of head biomechanics.
Objective
Computational studies of traumatic brain injury (TBI) hold great promise for injury prediction and prevention; however, the mechanical coupling between the skull and brain remains largely uncharacterized. In vivo measurement of relative skull and brain motion can provide insight into the mechanics of the skull-brain interface and can provide valuable parameters for models of TBI. Magnetic resonance elastography (MRE) is a noninvasive imaging modality that has been used to estimate the mechanical properties of soft biological tissue by measuring displacement from applied harmonic vibration.1 MRE has not yet been used to estimate head displacements in conjunction with brain motion. Challenges include phase wrapping2, voxel resolution, and low signal magnitude in bone. Alternatively, the motion of soft tissue surrounding the skull (scalp) can be measured and may enable estimation of skull motion. To assess the relationship between brain, skull, and scalp motion, we estimated rigid-body displacements of brain and scalp from MRE with low motion-encoding gradient (MEG) strength and compared with skull displacements estimated from an instrumented mouth guard containing three triaxial accelerometers.Methods
MRE was performed in five human subjects on a Siemens Trio® 3T MRI scanner using an echo-planar imaging (EPI) sequence. Imaging parameters included 3 MEG directions at a strength of 7 mT/m, 8 phase offsets, and 24 axial slice acquisitions with 3 mm isotropic voxels. The MEG strength was chosen to encode skull and scalp rigid-body motion, which is typically of higher amplitude than brain shear wave motion, without phase wrapping. Skull vibrations were induced at a frequency of 50 Hz through a commercially available system (ResoundantTM, Rochester, MN) using a “pillow” actuator (Mayo Clinic, Rochester, MN) at the back of the subject’s head.3 3D skull kinematics were estimated using three MRI-safe, triaxial accelerometers (TSD109C2-MRI, BIOPAC©, Goleta, CA) embedded in a mouth guard array (MGA) that included a commercial sports mouth guard and 3D-printed interface (Figure 1a). Scalp voxels with high signal amplitude and high motion amplitude at 50 Hz were selected as follows: the head was divided into four quadrants, anterior (A), right (R), left (L), and posterior (P), and scalp voxels in each quadrant were assigned a score by normalizing (1) MRE signal magnitude ($$$\alpha$$$) and (2) fraction of power in the FFT at 50 Hz ($$$\beta$$$) to the highest values in each quadrant and assigning each normalized quantity equal weighting. The 100 points in each quadrant with the highest scores were selected to give a total of 400 scalp points throughout the 24-slice image volume. MRE data from the brain and selected scalp voxels were fitted to a model of rigid-body motion to find expressions for rigid-body translation ($$$u$$$) and rotation ($$$\theta$$$). Skull displacements at four locations corresponding to the midpoint of each skull quadrant were reconstructed from accelerometer data and compared to displacements of adjacent voxels in the scalp and brain (Figure 1b). Displacement estimates in the right-left (RL), anterior-posterior (AP), and superior-inferior (SI) directions are sampled at 8 time points per period, (Figure 1c-d).Results
In harmonic motion, the 3D trajectories of points in the skull, scalp, and brain are represented as ellipses (Figures 2a-c). Scalp motion is larger in amplitude than brain motion and is in-phase with skull motion. For all three regions, anterior-posterior displacement ($$$u_{AP}$$$) was consistently the largest component of translation. Skull and scalp experienced higher amplitude displacements in the left-right ($$$u_{RL}$$$) and axial ($$$u_{SI}$$$) directions than the brain (Figure 3a). For all three regions, rotation about the left-right axis ($$$\theta_{RL}$$$, “yes nodding”) was consistently the largest rotation component. The scalp had higher $$$\theta_{RL}$$$ and $$$\theta_{SI}$$$ than the brain and skull (Figure 3b). Phase delay between anterior skull and scalp motion was consistently smaller than between brain and skull (Figure 3c).Discussion and Conclusion
Rigid-body displacements of the brain and scalp, estimated by MRE, are smaller than skull displacement estimated from accelerometers, though estimated scalp motion is closer in amplitude and phase to skull motion. However, there are also differences in the orientation of motion in both scalp and skull. Some experimental limitations are acknowledged: Estimates of skull motion assume perfect coupling between the skull and accelerometers; and scalp motion estimation by MRE is complicated by relatively low signal and possible partial volume effects. Despite these limitations, our initial results indicate consistent attenuation of motion transmitted from the skull to the brain and scalp, which has implications for head acceleration sensors designed to be mounted to the scalp.4 These simultaneous measurements of skull, brain, and scalp motion in vivo will enable better experimental measurements and improved simulations of TBI biomechanics.Acknowledgements
Funding: Financial support for this study was provided by NIH Grant R01 NS055951References
1. Manduca, A., et al., Med. Imag. Analys., 2001, 5(4): 237-254. 2. Barnhill, E., et al., Magn. Reson. Med., 2015, 73(6): 2321-2331. 3. Murphy, M. C., et al., J. Magn. Reson. Imag., 2011, 34(3): 494-498. 4. Wu, L.C., et al., Ann. Biomed. Eng., 2016, 44(4): 1234-1245.Figures
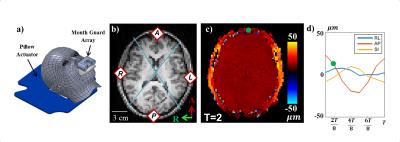
Figure 1: MRE and accelerometer data collection and
analysis. a) 3D rendering of the subject, pillow actuator, and MGA. b)
T1-weighted anatomical image with quadrants and corresponding reconstruction
points. c) Example MRE phase data encoding total AP displacement at 7 mT/m MEGS
at one time point (green dot in d). d) Components of displacement for anterior
scalp point (green dot in c).
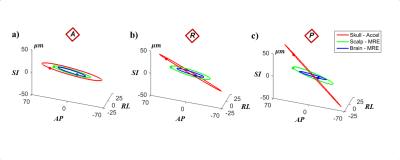
Figure 2: Elliptical trajectories of skull (red), scalp
(green), and brain (blue) motion at the a) anterior, b) right, and c) posterior
reconstruction points. Solid dots on the elliptical trajectory indicate the
position at reference time, t=0.
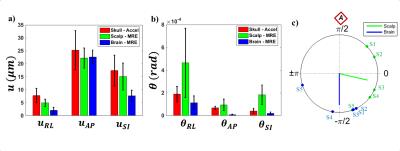
Figure 3: Rigid-body motion: a) translation and b)
rotation for skull (red), scalp (green), and brain (blue). Error bars indicate
standard deviation (n=5). c) Phase delay between anterior skull and scalp
motion (green) and anterior skull and brain motion (blue). Individual
observations are labeled by subject.