1132
Simultaneous Multislice Acquisition for Magnetic Resonance Elastography1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland, 2Division of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom, 3Department of Radiology, Academic Medical Center, Amsterdam, Netherlands
Synopsis
We propose the use of simultaneous multislice acquisition for Magnetic Resonance Elastography (MRE) of the full displacement vector field. To this end, multiband composite RF pulses are used for slice excitation in a fast, “eXpresso” type gradient echo based MRE acquisition. Slice and k-line dependent RF-phases are used to shift simultaneously acquired slices leading to improved unfolding performance (CAIPIRINHA). In this abstract, we demonstrate that multiband MRE with CAIPIRINHA can be used to acquire up to three slices simultaneously with only little SNR penalty in a gel phantom and show the feasibility to acquire full-brain images in-vivo.
Introduction
Magnetic Resonance Elastography (MRE) allows the in-vivo determination of the local tissue shear stiffness by time-resolved measurement of the 3D displacement field induced by an external actuator1. The need to balance resolution, scan duration, and achievable phase-to-noise ratio (PNR), has triggered the development of new actuator systems2–5, better wave inversion algorithms6–9, and improved acquisition techniques3,10–14. In this work, we focus on the efficient readout in multislice MRE through acquisition with multiband RF composite pulses exciting multiple slices simultaneously and subsequent unfolding of the images using coil sensitivity maps15. We further use CAIPIRINHA to improve signal unfolding performance through reduction of the geometry factors16.Theory
Multiband excitation utilizes modulated RF pulses in the time-domain to excite multiple parallel slices simultaneously. The image reconstructed in the j-th coil $$$S_j\left(\vec{r}\right)$$$ is thus a superposition of the signals of the simultaneously excited slices $$$n$$$ and is given by $$S_j\left(\vec{r}\right)=\sum_nC_j\left(\vec{r}-\vec{x}_n\right)\rho\left(\vec{r}-\vec{x}_n\right),$$ where $$$C_j\left(\vec{r}\right)$$$ denotes the coil sensitivity of the j-th coil and $$$\rho\left(\vec{r}\right)$$$ is the actual image. For conventional multiband acquisition, $$$\vec{x}_n=d_n\hat{e}_z$$$ is the position of the slices along the slice encoding direction. The unfolding of the signals is achieved through solution of the inverse encoding problem for each pixel15. The noise amplification in the unfolded images compared to sequentially acquired slices is then given by the geometry factor$$g=\sqrt{\text{diag}\left(\hat{C}^\text{H}\hat{C}\right)\cdot\text{diag}\left(\left(\hat{C}^\text{H}\hat{C}\right)^{-1}\right)}.$$CAIPIRINHA utilizes additional slice-dependent RF phase modulation in phase-encoding direction to induce a slice dependent field-of-view shift16, thereby drastically increasing sensitivity differences and hence SNR performance.Methods
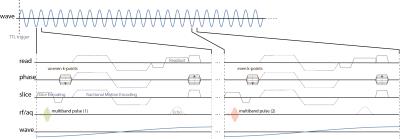
Multiband RF pulses with slice-dependent phase-modulation were implemented on a Philips Achieva 3T system with an 8-channel head coil and wave data were acquired in an ultrasound gel phantom and in the brain of two volunteers. All measurements were performed using the “eXpresso” sequence, i.e. a spoiled, fractional GRE-MRE sequence (Figure 1) with a wave frequency of 30 Hz, Cartesian readout, and two shots per wave cycle17,18. The wave propagation was captured eight times per wave cycle and the motion encoding gradients were applied along each of the main gradient axes sequentially. A reference scan without motion sensitization was also acquired to correct for field inhomogeneity. A dual electro-mechanical actuator setup fixed to the head coil was used pressing against the skull from each side. The full set of scan parameters is given in Table 1.Results and Discussion
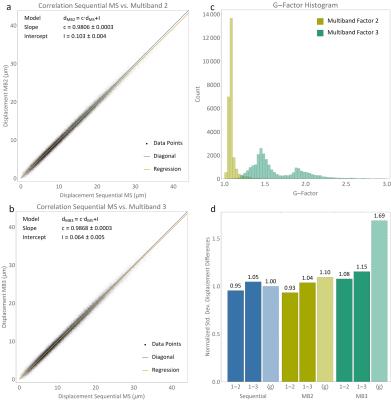
In Figure 2, correlation plots of reconstructed wave displacement magnitudes for the phantom scans are shown comparing sequential multislice (MS) to multiband acquisition with (a) an acceleration factor of 2 (MB2) and (b) an acceleration factor of 3 (MB3). Both methods are highly correlated to non-accelerated imaging. In Figure 2c, g-factor histograms are shown indicating noise enhancement factors for MB2 smaller 1.5 and 2.8 for MB3. In Figure 2d, measured standard deviation of displacement magnitude differences between a reference scan and two additional scans with equal scan parameters are compared to g-factors for MS, MB2, and MB3. The standard deviation was normalized to the average deviation in the MS scans for comparability. For both, MB2 and MB3, g-factors indicate much higher noise increase than reflected in respective standard deviations, indicating that other error sources, such as the coupling of the transducer and phantom as well as low phase encoding efficiency, are dominating over unfolding performance.
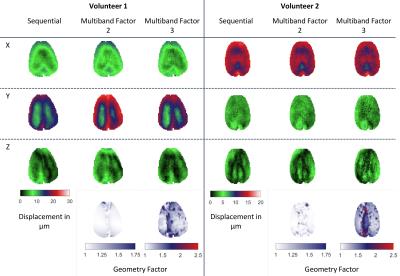
In Figure 3, in-vivo displacement maps for one selected slice and all three motion encoding directions are presented for MS MRE as well as MB2 and MB3 measurements. Additionally, g-factor maps are shown for MB2 and MB3 with overall g-factors smaller than 1.75 for MB2 and 2.5 for MB3. Displacement maps are in good agreement between MS, MB2, and MB3 with noise being more pronounced in MB2 and MB3 measurements. Due to the actuator setup being fixed to the head coil and volunteer movement, wave coupling performance varied between subsequent scans leading to stronger coupling and hence higher displacements in the MB2 scan of volunteer 1.
Conclusions
We have demonstrated the feasibility of multiband acquisition with CAIPIRINHA for fast, SNR-efficient MRE of the brain, allowing for the acquisition of up to three slices simultaneously. Higher number of simultaneously acquired slices as well as increased unfolding performance can be achieved using receive coils with more than 8 channels such as 32-channel coils, which have been successfully used in SMS-fMRI acquisitions19. The demonstrated increase in acquisition efficiency can be used to allow for full-brain coverage or increased patient comfort through reduction of total scan duration.Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.References
1. Muthupillai, R. et al. Magnetic resonance imaging of transverse acoustic strain waves. Magn. Reson. Med. 36, 266–274 (1996).
2. McGrath, D. M. et al. Evaluation of wave delivery methodology for brain MRE: Insights from computational simulations. Magn. Reson. Med. 0, (2016).
3. Anderson, A. T. et al. Observation of direction-dependent mechanical properties in the human brain with multi-excitation MR elastography. J. Mech. Behav. Biomed. Mater. 59, 538–546 (2016).
4. Fehlner, A. et al. Cerebral multifrequency MR elastography by remote excitation of intracranial shear waves. NMR Biomed. 28, 1426–1432 (2015).
5. Numano, T., Mizuhara, K., Hata, J., Washio, T. & Homma, K. A simple method for MR elastography: A gradient-echo type multi-echo sequence. Magn. Reson. Imaging 33, 31–37 (2015).
6. Honarvar, M., Rohling, R. & Salcudean, S. E. A comparison of direct and iterative finite element inversion techniques in dynamic elastography. Phys. Med. Biol. 61, 3026–3048 (2016).
7. Tzschätzsch, H., Guo, J., Dittmann, F., Braun, J. & Sack, I. in Bildverarbeitung für die Medizin 2006 p3–7 (Springer Berlin Heidelberg, 2016).
8. Honarvar, M., Lobo, J., Mohareri, O., Salcudean, S. E. & Rohling, R. Direct vibro-elastography FEM inversion in Cartesian and cylindrical coordinate systems without the local homogeneity assumption. Phys. Med. Biol. 60, 3847–3868 (2015).
9. Petrov, A. Y., Docherty, P. D., Sellier, M. & Chase, J. G. Multi-frequency inversion in Rayleigh damped Magnetic Resonance Elastography. Biomed. Signal Process. Control 13, 270–281 (2014).
10. Johnson, C. L. et al. Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction. Magn. Reson. Med. 70, 404–412 (2013).
11. Klatt, D., Yasar, T. K., Royston, T. J. & Magin, R. L. Sample interval modulation for the simultaneous acquisition of displacement vector data in magnetic resonance elastography: theory and application. Phys. Med. Biol. 58, 8663–75 (2013).
12. Klatt, D., Johnson, C. L. & Magin, R. L. Simultaneous, multidirectional acquisition of displacement fields in magnetic resonance elastography of the in vivo human brain. J. Magn. Reson. Imaging 42, 297–304 (2015).
13. Johnson, C. L. et al. 3D multislab, multishot acquisition for fast, whole-brain MR elastography with high signal-to-noise efficiency. Magn. Reson. Med. 71, 477–485 (2014).
14. Yasar, T. K., Klatt, D., Magin, R. L. & Royston, T. J. Selective spectral displacement projection for multifrequency MRE. Phys. Med. Biol. 58, 5771–81 (2013).
15. Larkman, D. J. et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging 13, 313–317 (2001).
16. Breuer, F. A. et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 53, 684–691 (2005).
17. Rump, J., Klatt, D., Braun, J., Warmuth, C. & Sack, I. Fractional encoding of harmonic motions in MR elastography. Magn. Reson. Med. 57, 388–395 (2007).
18. Garteiser, P. et al. Rapid acquisition of multifrequency, multislice and multidirectional MR elastography data with a fractionally encoded gradient echo sequence. NMR Biomed. 26, 1326–1335 (2013).
19. Zahneisen, B., Poser, B. A., Ernst, T. & Stenger, A. V. Simultaneous Multi-Slice fMRI using spiral trajectories. Neuroimage 92, 8–18 (2014).
Figures