1123
High Resolution Multi-shot Diffusion Imaging at 7T without Navigators1Department of Radiology, University of Iowa, Iowa City, IA, United States, 2University of Iowa, Iowa City, IA, United States, 3GE Healthcare
Synopsis
The higher signal-to-noise ratio (SNR) offered by the ultra-high field (UHF) strengths are often exploited to improve the spatial resolution capabilities of several MR imaging modalities. However, SNR advantage of UHF scanners do not often translate to improved diffusion weighted images (DWIs), especially using conventional single-shot echo-planar imaging-based acquisitions. The presence of diffusion gradients limit the lowest echo-time (TE) achievable, while the shortened T2 and T2* values lead to faster decay of the MRI signal, both of which are detrimental to the already signal-starved DWIs. We propose a short-TE acquisition based on multi-shot EPI and partial Fourier acquisition to enable high resolution diffusion imaging at 7T that does not need navigator scans or phase calibration.
Introduction
The higher signal-to-noise ratio (SNR) offered by the ultra-high field (UHF) strengths are often exploited to improve the spatial resolution capabilities of several MR imaging modalities. However, SNR advantage of UHF scanners do not often translate to improved diffusion weighted images (DWIs), especially using conventional single-shot echo-planar imaging-based acquisitions. The presence of diffusion gradients limit the lowest echo-time (TE) achievable, while the shortened T2 and T2* values lead to faster decay of the MRI signal, both of which are detrimental to the already signal-starved DWIs. We propose a short-TE acquisition based on multi-shot EPI and partial Fourier acquisition to overcome many of the above issues to enable high resolution diffusion imaging at 7T. This method is particularly distinct from similar methods proposed to achieve the same due to the absence of navigator scans or phase calibration1,2.Methods
The reduced readout of the multi-shot diffusion-weighted (MS-DW) acquisition leads to higher SNR and lower T2* artifacts, especially on UHF scanners. However, the main drawback of the MS-DW acquisition is its sensitivity to motion artifacts. To compensate for the phase arising from motion, most MS-DW acquisitions are accompanied by navigator scans which provide an estimate of the phase. We show that the DWIs from the MS-DW acquisition can be reconstructed with inherent motion compensation with the simplicity of a regularized SENSE reconstruction without the need of navigators. Our method exclusively skip the explicit phase calibration that is required with the current MS-DW reconstructions. We achieve this by performing matrix completion on a structured matrix formed from the k-space data of the shots; this structured matrix is the convolution matrix that is being acted upon by the motion-phase filter in the frequency domain.
Denoting the DWI of shots $$$i,j$$$ by $$$m_i(x),m_j(x)$$$ and their corresponding k-space data by $$$\widehat{m_i}[k],\widehat{m_j}[k]$$$, we can derive the following relation:$$\begin{equation}{\bf{H}}(\widehat{m_{i}}) \cdot \widehat \phi_j [{\bf{k}}]- {\bf{H}}(\widehat{m_{j}}) \cdot \widehat \phi_i[{\bf{k}}]=0, \end{equation}$$where $$${\bf{H}}(\widehat{m_{i}})$$$ and $$${\bf{H}}(\widehat{m_{j}})$$$ are the Hankel-structured convolution matrices of the k-space shots $$$\widehat{m_{i}}[k]$$$ and $$$\widehat{m_{j}}[k]$$$ and $$$\widehat \phi_i [{\bf{k}}]$$$ and $$$\widehat \phi_j [{\bf{k}}]$$$ are the motion-phase filters associated with the shots respectively3. Generalizing the above analysis to $$$N_s$$$ shots, we can derive a block-Hankel structured matrix $$${\bf{H_1}}$$$, comprising of the convolution matrices of all the $$$N_s$$$ shots: $$\begin{equation}{\bf{H_1}}=[{\bf{H}}(\widehat{m_{1}})\hspace{5mm}{\bf{H}}(\widehat{m_{2}})\hspace{5mm}\cdots\hspace{5mm}{\bf{H}}(\widehat{m_{N_s}})],\end{equation}$$ which will be of low-rank by construction. By performing matrix completion on $$${\bf{H_1}}$$$, we recover the motion-compensated k-space data of each shot without the knowledge of the motion-induced phases.
To further shorten the TE, we also adopt a partial Fourier-based acquisition. To improve the reconstruction accuracy, we employ an additional smoothness regularization during the reconstruction and formulate the reconstruction problem as $$\begin{equation}\hat{\tilde {\bf m}}= \text{argmin}_{{\bf \hat{m}}} {||\bf{{\cal{A}}(\hat{ m})-\hat y}}||^2_{\ell_2} + \lambda||{\bf{\bf{H_2}}}(\hat{ m})||_*,\end{equation}$$ where $$${\bf{H_2}}$$$ is the block-Hankel-structured matrix derived from the x- and y- derivatives of the shot DWIs such that $$\begin{equation}{\bf{H_2}}= \begin{bmatrix} {\bf{H}}(\widehat{\partial_1 m_1}) & {\bf{H}}(\widehat{\partial_1 m_2}) & ... & {\bf H}(\widehat{\partial_1 m_{N_s}}) \\{\bf{H}}(\widehat{\partial_2 m_1}) & {\bf{H}}(\widehat{\partial_2 m_2}) & ... & {\bf H}(\widehat{\partial_2 m_{N_s}})\end{bmatrix}.\end{equation}$$Here, $$$\bf{\widehat y}$$$ is the measured multi-channel multi-shot k-space data. The first term imposes data consistency to the measured k-space data using a regular SENSE formulation. The operator $$$\bf{{\cal{A}}}$$$ represents: $$$\bf{{\cal{M}}}\circ\bf{{\cal{F}}}\circ\bf{{\cal{S}}}\circ\bf{{\cal{F}}^{-1}}$$$ where $$$\bf{{\cal{F}}}$$$ and $$$\bf{{\cal{F}}^{-1}}$$$ represent the Fourier and the inverse Fourier transform operations respectively, $$$\bf{{\cal{S}}}$$$ represents coil sensitivities, and $$$\bf{{\cal{M}}}$$$ represents the k-space sampling mask of each shot. $$$ \lambda$$$ is a regularization parameter. The proposed method recovers the multi-shot k-space data corresponding to the motion-compensated DWI, from which the magnitude DWI can be recovered by taking the inverse Fourier transform and doing a sum-of-squares.
Diffusion data was collected on a GE MR950 7T scanner at the University of Iowa with maximum gradient strength 50mT/m and maximum slew rate 200mT/m/ms. The 2/32-channel Tx/Rx head coil was used in Tx mode. A 4-shot dual-spin-echo diffusion sequence with b-value=700s/mm2, 25 diffusion directions and one non-DWI was used. The imaging parameters were: FOV=210mmx210mm; matrix size=256x256, slice thickness=2mm, TE=78 ms with pf oversampling of 20 lines and NEX=3. No special navigator scans or auto-calibration lines were collected.
Results
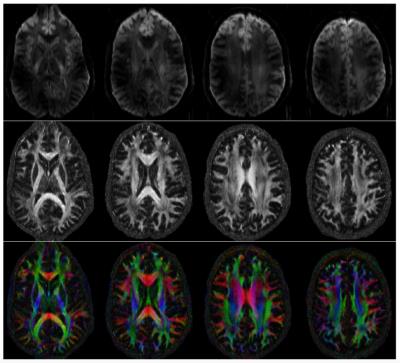
Figure 1 shows the reconstruction of a DWI from four different slices as well as the fractional anisotropy maps and the direction encoded color maps reconstructed using the proposed method after averaging all the three acquisitions. The images are free of motion-induced artifacts and show detailed fiber microstructure and provide high quality DWIs.Conclusion
We proposed direct reconstruction scheme for MS-DW acquisition that does not require motion-phase calibration and can reconstruct motion-compensated DWIs from partially acquired k-space data. The short TE afforded by the above scheme can enable the acquisition of high spatial resolution DWIs on UHF scanners without the need for navigators.Acknowledgements
No acknowledgement found.References
1. Wenchuan Wu, Benedikt A. Poser, Gwenaëlle Douaud, Robert Frost, Myung-Ho In, Oliver Speck, Peter J. Koopmans, Karla L. Miller, High-resolution diffusion MRI at 7T using a three-dimensional multi-slab acquisition, NeuroImage, Volume 143, December 2016, Pages 1-14, ISSN 1053-8119, http://dx.doi.org/10.1016/j.neuroimage.2016.08.054.
2. Jeong, H.-K., Gore, J. C. and Anderson, A. W. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T., (2013), Magn Reson Med, 69: 793–802. doi:10.1002/mrm.24320
3. Mani, M., Jacob, M., Kelley, D. and Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. doi: 10.1002/mrm.26382, 2016
Figures