1094

Three-Dimensional Multiplexed Sensitivity Encoding and Reconstruction (3D-MUSER): 3D Phase Correction for 3D Multi-shot DWI

Hing-Chiu Chang¹, Edward S. Hui^1,2, Xiaoxi Liu¹, Pui-Wai Chiu¹, and Nan-kuei Chen^3,4

¹Department of Diagnostic Radiology, The University of Hong Kong, Hong Kong, Hong Kong, ²The State Key Laboratory of Brain and Cognitive Sciences, The University of Hong Kong, Hong Kong, ³Department of Biomedical Engineering, University of Arizona, Tucson, AZ, United States, ⁴Brain Imaging and Analysis Center, Duke University Medical Center, Durham, NC, United States

Synopsis

3D interleaved DW-EPI with 2D multiplexed sensitivity encoding has been shown useful in achieving submillimeter DTI. Similar to other 3D DTI techniques, 2D phase variation is only considered in eliminating aliasing artifacts, thereby limiting feasible slab thickness. 3D phase correction is a potential strategy to significantly improve the image quality and feasible slab thickness of 3D DTI. To enable 3D phase correction, we develop a new reconstruction algorithm, and implement an EVI-based navigator echo for direct 3D phase measurement. Quantitative results show that the proposed algorithm can effectively eliminate aliasing artifacts and signal corruptions due to 3D inter-shot phase variations.

Introduction

Recently, 3D DTI at submillimeter isotropic resolution was successfully achieved using 3D interleaved DW-EPI with 2D multiplexed sensitivity encoding (2D-MUSE)^1,2. Similar to other reconstruction algorithms for multi-shot DWI, 2D phase variation is only considered in eliminating aliasing artifacts, thereby limiting feasible slab thickness³. Instead of considering 2D inter-shot phase variation, either cardiac reordering strategy or cardiac gating has been used to improve the image quality of thin-slab 3D multi-shot DW-EPI by reducing the influence of intra-slab phase variation^4,5. 3D phase correction is thus a potential strategy to significantly improve the image quality of 3D multi-shot DWI. To practically enable 3D phase correction and improve the feasible slab thickness for 3D interleaved DW-EPI, first, we propose a new algorithm, 3D multiplexed sensitivity encoding and reconstruction (3D-MUSER), to reconstruct 3D interleaved DW-EPI data in the hybrid k-space by taking 3D inter-shot phase variation into account. Second, we implement an echo-volume imaging (EVI) -based navigator echo to directly measure 3D volume phase.

Methods

3D-MUSER: The proposed 3D-MUSER extends the framework of 2D-MUSE from an image-domain-based reconstruction (i.e., solving aliased pixels) to a hybrid k-space-based reconstruction. The k-space signal acquired from γ^th coil element (with coil sensitivity C_γ) for j^th k_y interleaf at specific k_z encoding step of 3D interleaved DW-EPI can be written as:

$$$S_{\gamma}\left(k_{x},k_{y|j},k_{z}\right)=\int_{}^{} \int_{}^{}\int_{}^{}\rho(x,y,z)C_{\gamma}(x,y,z)e^{\theta_{k_{y|j},k_{z}}(x,y,z)}e^{i2\pi(k_{x}x+k_{y|j}y+k_{z}z)}dxdydz$$$ (1)

where $$$\theta_{k_{y|j},k_{z}}(x,y,z)$$$ represents 3D inter-shot phase variation.

Eq. 1 can be simplified by applying 1D-FT along k_x and be subsequently rewritten as:

$$$S_{\gamma,k_{y|j},k_{z}}=\mathbf{F}_{k_{y|j},k_{z}} \Theta_{k_{y|j},k_{z}} \mathbf{C}_{\gamma} \overline{\rho} = \mathbf E _{\gamma,k_{y|j},k_{z}}\overline{\rho}$$$ (2)

where $$$\mathbf{F}_{k_{y|j},k_{z}}$$$ denotes an operator of 2D FT along k_y|j and k_z (k_y-k_z plane at each x’ location). The intensities of all pixels for a y-z plane at location x' can be formulated as a minimization problem $$$\overline{\rho}=arg_{\rho}min||\mathbf{E\overline{\rho}-\mathbf{S}}||_2^2$$$, which can be solved by using conjugate gradient least-squares.

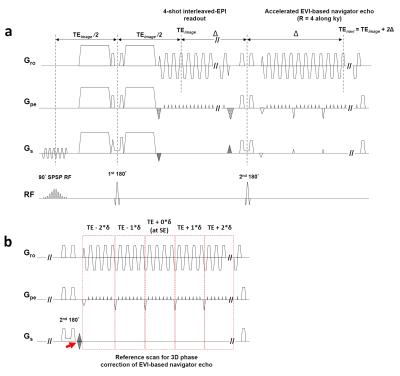
Pulse sequence design: An EVI-based navigator echo was equipped into 3D interleaved DW-EPI sequence as shown as in Figure 1a. To minimize the echo time of navigator echo, we used three strategies: 1) small matrix size along y and z (32×12); 2) partial k-space sampling along k_z (70%); and 3) high acceleration factor along k_y (R=4).

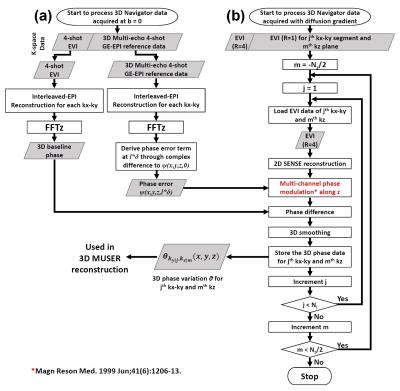
Reconstruction of navigator echo: First, a 3D multi-echo interleaved GE-EPI reference scan (performed only during acquisition of b = 0) shown in Figure 1b was used to measure the phase errors. Second, all accelerated navigator data were reconstructed and performed phase correction using the flowchart shown in Figure 2.

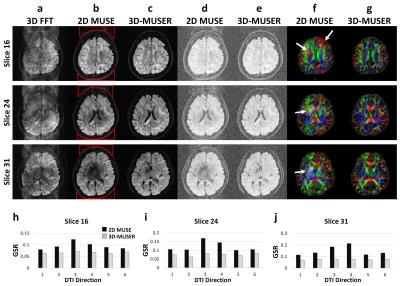
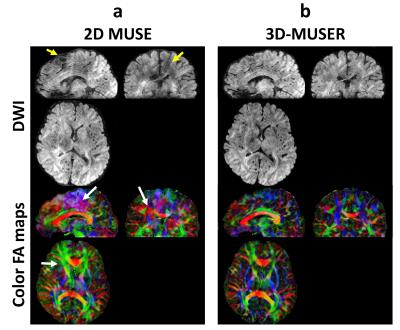
Experiments: To evaluate the efficacy of phase correction for 3D DTI, we acquired two sets of 3D 4-shot interleaved DW-EPI data with 1.6 mm (slab thickness = 60mm, # of k_z = 38, x-y matrix = 128, TR = 1000ms, b = 1000, # of DTI = 6) and 1.3 mm (slab thickness = 98.8mm, # of k_z = 76, x-y matrix = 128, TR = 500ms, b = 800, # of DTI = 7) isotropic voxel using a 1.5T MRI scanner (GE HDxt). After acquisition, two data sets were reconstructed using either 2D-MUSE or 3D-MUSER. The ghost-to-signal ratios (GSR) of 1.6 mm isotropic voxel data were measured and then compared using a bar plot. The color FA maps were calculated from all reconstructed images for visual comparison.

Results

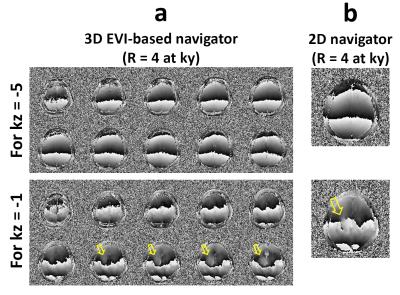
Figure 3 shows two representative sets of volume phase images in the absence and presence of intra-slab phase variations. Figure 4 shows 1.6-mm isotropic diffusion-weighted images reconstructed using FFT, 2D-MUSE, and 3D-MUSER. Figure 5 shows that near whole-brain coverage 3D DTI without signal corruption and slab boundary artifacts could be achieved by using 3D-MUSER for single slab acquisition (98.8 mm).

Discussion and Conclusion

3D-MUSER can take non-linear 3D inter-shot phase variations into account, thereby eliminating the aliasing artifacts and signal corruptions due to 3D inter-shot phase variations in 3D interleaved DW-EPI acquisition. The quantitative measurements in Fig.4 show that 3D-MUSER can effectively correct inter-shot phase variations in extreme thick slab thickness.

In this study, we implemented an EVI-based navigator echo to measure 3D inter-shot phase variations. Our results show that EVI-based navigator echo is sufficient to measure low-frequency nonlinear phase variations. We would like to point out that, although the cardiac gating was not needed in our current study at 1.5 Tesla, it may be integrated with our 3D-MUSER method in future studies at high magnetic fields and high b-values to minimize the potential artifacts due to highly nonlinear phase errors. In addition, the SNR efficiency associated with improved feasible slab thickness needs to be investigated.

In conclusion, 3D-MUSER is an effective 3D phase correction method for 3D interleaved DW-EPI acquisition with improved feasible slab thickness.

Acknowledgements

No acknowledgement found.

References

1. Chang HC, Sundman M, Petit L, Guhaniyogi S, Chu ML, Petty C, Song AW, Chen NK. Human brain diffusion tensor imaging at submillimeter isotropic resolution on a 3Tesla clinical MRI scanner. Neuroimage 2015;118:667-675.

2. Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 2013;72:41-47.

3. Engstrom M, Skare S. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn Reson Med 2013;70(6):1507-1514.

4. Frost R, Miller KL, Tijssen RH, Porter DA, Jezzard P. 3D multi-slab diffusion-weighted readout-segmented EPI with real-time cardiac-reordered K-space acquisition. Magn Reson Med 2014;72(6):1565-1579.

5. Van AT, Hernando D, Sutton BP. Motion-induced phase error estimation and correction in 3D diffusion tensor imaging. IEEE Trans Med Imaging 2011;30(11):1933-1940.

Figures

Figure 1: (a) 3D interleaved DW-EPI pulse sequence equipped with EVI-based navigator echo. (b) EVI-based navigator echo can be switched to 3D multi-echo interleaved GE-EPI reference scan to measure the phase accumulations due to field inhomogeneity. The blip gradients along z for EVI acquisition will be switched to slice encoding gradient (red arrow).

Figure 2: Flowchart of reconstruction of EVI-based navigator data. (a) The 4-shot EVI-based navigator data and 3D multi-echo 4-shot GE-EPI reference data acquired at b = 0 s/mm² are processed separately to generate i) 3D baseline phase map, and ii) 3D phase accumulation Ψ(x,y,z,l*δ) due to field inhomogeneity for each k_z acquisition of EVI-based navigator. (b) Reconstruction of accelerated EVI-based navigator data acquired at different k_x-k_y segment and k_z encoding. The measured 3D phase variation maps Θ_ky_|j,_kz_|m(x,y,z) for all k_x-k_ysegments with different k_z encoding are subsequently used in 3D-MUSER to eliminate the aliasing artifacts due to inter-shot phase variations.

Figure 3: (a) Two representative sets of volume phase images in the absence (upper panel) and presence of intra-slab phase variations (yellow arrows at lower panel) measured from a 60 mm slab using EVI-based navigator echo. (b) 2D navigator phase images corresponding to (a) shows that the intra-slab phase variations were collapsed along z direction (yellow arrow at lower panel).

Figure 4: 1.6-mm isotropic diffusion-weighted images of three representative slices reconstructed from a 60-mm slab (with 38 encoding steps) with (a) FT, (b) 2D-MUSE, and (c) 3D-MUSER. The red ROIs in (b) were used to measure GSR for both 2D-MUSE and 3D-MUSER reconstructed images. (d) and (e) show the same images in (b) and (c) but with a different display scale that can better illustrate background artifacts. (f) and (g) show the colored FA maps calculated from 2D-MUSE and 3D-MUSER reconstructed image data, respectively. (h)-(j) show quantitative comparisons of GSRs for 6 different diffusion directions of three representative slices.

Figure 5: 1.3-mm isotropic diffusion-weighted images reconstructed from a 98.8-mm single slab 3D DTI data with either (a) 2D-MUSE or (b) 3D- MUSER. The colored FA maps calculated from 7 diffusion directions of each reconstructed data set were shown at bottom panels. The whole brain 3D DTI without signal corruption and banding artifacts could be achieved by using 3D-MUSER for single slab data.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1094