1092
Isotropic Diffusion Weighted MRI (IDWI) – a novel, efficient clinical method for quantifying orientationally-averaged features of water diffusion in tissues1NIBIB, National Institutes of Health, Bethesda, MD, United States, 2NINDS, National Institutes of Health, Bethesda, MD, United States, 3NICHD, National Institutes of Health, Bethesda, MD, United States
Synopsis
We propose a novel, efficient diffusion method, called isotropic diffusion weighted MRI (IDWI), for measuring orientationally-averaged properties of tissue water diffusion, free from modulations due to anisotropy. Using efficient diffusion gradient sampling schemes, IDWI rapidly and accurately quantifies the mean apparent diffusion coefficient (mADC) over a wide range of b-values, along with other important rotation-invariant intrinsic microstructural parameters, such as the mean t-kurtosis. The ability to efficiently and effectively remove modulations due to anisotropy in images with high-b values may improve existing diffusion MRI techniques and spur the development and clinical translation of new methods with improved biological specificity.
Purpose
We propose a novel, efficient diffusion method, called isotropic diffusion weighted MRI (IDWI), for measuring orientationally-averaged diffusion MRI signals up to very large b-values, free from modulations due to anisotropy. Using efficient diffusion gradient sampling schemes, IDWI rapidly and accurately quantifies the mean apparent diffusion coefficient (mADC)1 over a wide range of b-values, along with other important rotation-invariant intrinsic microstructural parameters derived from higher-order diffusion tensors (HOTs)2,3, such as the generalized trace4, or the mean t-kurtosis5.Methods
We acquired high-quality preclinical and clinical diffusion MRI datasets in fixed ferret brain (250x250x250µm3, TE/TR=36/700ms, bmax=13500mm2/s) and in vivo human brain (2.5x2.5x5mm3, TE/TR=93/7000ms, bmax=6000mm2/s), respectively. For both ex vivo and in vivo experiments we obtained two DWI datasets:
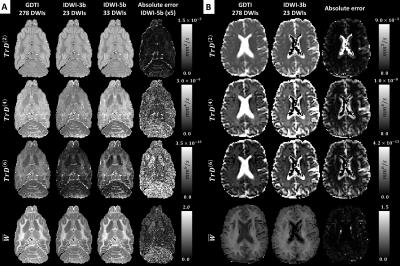
1. One dataset was acquired using dense angular sampling at multiple b-values to allow measurement of mADC-weighted diffusion weighted images (DWIs). The dataset was analyzed with generalized diffusion tensor imaging (GDTI)2 to explicitly measure the HOTs up to order n=6, their generalized Traces, $$$TrD^{(n)}$$$, and the mean t-kurtosis, ($$$\overline{W}$$$). The generalized trace $$$TrD^{(n)}$$$ was computed form the elements of the n-th order diffusion tensor $$$D_{n_{x}n_{y}n_{z}}^{(n)}$$$ $$TrD^{(n)}=\sum_{n_{x}+n_{y}+n_{z}=n}^{}K_{n_{x}n_{y}n_{z}}\mu_{\frac{n_{x}}{2}\frac{n_{y}}{2}\frac{n_{z}}{2}}D_{n_{x}n_{y}n_{z}}^{(n)}$$, where $$$\mu_{n_{x}n_{y}n_{z}}=\frac{n!}{n_{x}!n_{y}!n_{z}!}$$$, and $$$K_{n_{x}n_{y}n_{z}}=1$$$ when $$$n_{x}$$$, $$$n_{y}$$$, and $$$n_{z}$$$ are all even, and 0 otherwise.
2. A second dataset was acquired using efficient sampling Schemes 1, 2, and 3 (Fig.1) with a maximum of 13 orientations, at each of the 3 or 5 different b-values over the same range as in the GDTI experiments. From this IDWI data we generated mADC-weighted DWIs at each b-value using linear combinations of the log signal attenuations averaged over the signals acquired with orientations from Schemes 1, 2, and 3, denoted by M3(b), M4(b), and M6(b). respectively (Fig.2). From the mADC-weighted DWIs we computed $$$TrD^{(n)}$$$ and $$$\overline{W}$$$ for comparison with GDTI-derived values.
Results
The high accuracy and rotation invariance of ID-MRI over a large range of b-values is validated in Fig.3. In fixed ferret and live human brain tissues orientationally-averaged (i.e., mADC-weighted) DWIs derived from densely sampled GDTI data and from IDWI data acquired with different rotations of the sampling schemes in Fig.1, are in excellent agreement. Moreover, despite requiring significantly fewer DWIs, rotation-invariant microstructural parameters such as and derived with IDWI showed similar values to those computed by explicitly measuring the HOT components with GDTI (Fig.4). Fig.4 also illustrates the benefit of including a larger number of b-values to stabilize the measurement of from orientation-averaged DWIs, in agreement with5,6. Compared to the fixed-brain experiment, in vivo IDWI showed slightly larger errors, especially at tissue boundaries, likely due to subject motion during the duration of the scan (Fig.3 and Fig.4).
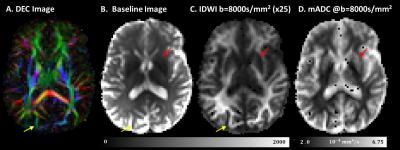
The clinical potential of IDWI is best illustrated with measurements obtained at very high b-values (Fig.5). The in vivo (mADC-weighted) IDWI signal at b = 8500s/mm2 reveals a tissue contrast that resembles the fractional anisotropy (FA)7 but may be less modulated by architectural features of the tissue (Fig.5 yellow arrows). At the same time, the mADC measured at high b-value (Fig.5D) shows improved contrast around the putamen and globus pallidus compared to the T2-weighted image (Fig.5 red arrows).
Discussion
Our results indicate that in both micro-imaging and clinical experiments, signal modulations from bulk anisotropy of water diffusion can be accurately eliminated using a 6th-order tensor model. Despite the structural and architectural complexities of brain tissues, orientationally-averaged diffusion signals can be obtained from as few as 13 measurements even at large diffusion sensitization, while for smaller b-values fewer measurements are needed.
The efficient IDWI sampling schemes can reduce total scan duration (and subject/physiological motion) enabling a rapid and accurate assessment of orientationally-averaged water mobilities in clinical exams. Further acceleration can be achieved with single-shot isotropic diffusion techniques8-10.
IDWI extends the clinical assessment of eloquent rotation-invariant parameters, such as the mADC, which has provided a sensitive, robust, reliable and quantitative clinical imaging biomarker for non-invasive detection and characterization of hypoxic ischemic brain injury11, cancers, and other pathologies12. Moreover, IDWI may enable new whole-brain clinical applications that require dense sampling of the orientation-averaged diffusion signal decays as a function of b-value13,14.
Conclusions
IDWI provides a fast and accurate solution to assessing orientationally-averaged properties of tissue water diffusion both in fixed brain specimen and in human subjects. The ability to efficiently and effectively remove modulations due to anisotropy in images with high-b values may improve existing diffusion MRI techniques and spur the development and clinical translation of new methods with improved biological specificity.Acknowledgements
This work was supported by the Intramural Research Programs of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) and the National Institutes of Biomedical Imaging and Bioengineering (NIBIB).References
1 Basser, P. J., Mattiello, J. & LeBihan, D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 103, 247-254 (1994).
2 Liu, C., Bammer, R. & Moseley, M. E. Generalized Diffusion Tensor Imaging (GDTI): A Method for Characterizing and Imaging Diffusion Anisotropy Caused by Non-Gaussian Diffusion. Israel Journal of Chemistry 43, 145-154, doi:10.1560/hb5h-6xbr-1aw1-lnx9 (2003).
3 Liu, C., Bammer, R., Acar, B. & Moseley, M. E. Characterizing non-gaussian diffusion by using generalized diffusion tensors. Magn Reson Med 51, 924-937, doi:10.1002/mrm.20071 (2004).
4 Özarslan, E., Vemuri, B. C. & Mareci, T. H. Generalized scalar measures for diffusion MRI using trace, variance, and entropy. Magn Reson Med 53, 866-876, doi:10.1002/mrm.20411 (2005).
5 Hansen, B., Lund, T. E., Sangill, R. & Jespersen, S. N. Experimentally and computationally fast method for estimation of a mean kurtosis. Magn Reson Med 69, 1754-1760, doi:10.1002/mrm.24743 (2013).
6 Hansen, B. et al. Experimental considerations for fast kurtosis imaging. Magn Reson Med, n/a-n/a, doi:10.1002/mrm.26055 (2015).
7 Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys J 66, 259-267, doi:10.1016/S0006-3495(94)80775-1 (1994).
8 Mori, S. & Van Zijl, P. C. M. Diffusion Weighting by the Trace of the Diffusion Tensor within a Single Scan. Magn Reson Med 33, 41-52, doi:10.1002/mrm.1910330107 (1995).
9 Wong, E. C., Cox, R. W. & Song, A. W. Optimized isotropic diffusion weighting. Magn Reson Med 34, 139-143 (1995).
10 Avram, A. V., Sarlls, J. E., Freidlin, R. Z. & Basser, P. J., Clinical feasibility of high-resolution single-shot diffusion tensor trace -weighted (ssTW) MRI, in The 22nd Annual Meeting of the International Society for Magnetic Resonance in Medicine 2067 (Salt Lake City, USA, 2013).
11 Moseley, M. E. et al. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med 14, 330-346 (1990).
12 Le Bihan, D. et al. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 161, 401-407 (1986).
13 Ronen, I., Moeller, S., Ugurbil, K. & Kim, D.-S. Investigation of multicomponent diffusion in cat brain using a combined MTC-DWI approach. Magn Reson Imaging 24, 425-431, doi:10.1016/j.mri.2005.12.022 (2006).
14 Pfeuffer, J., Provencher, S. W. & Gruetter, R. Water diffusion in rat brain in vivo as detected at very large b values is multicompartmental. Magn Reson Mater Phy 8, 98-108 (1999).
Figures
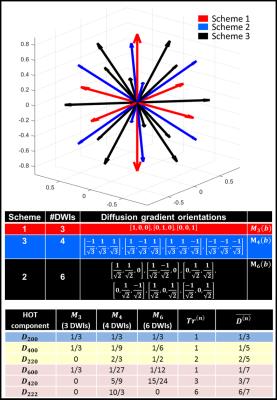
Figure 1: Diffusion gradient orientations for measuring the average log signal attenuations M3(b), M4(b), and M6(b), using the efficient IDWI sampling Schemes 1, 2, and 3. The relative weightings of unique tensor components in the expressions of the three log signal attenuation averages, M3(b), M4(b), and M6(b), as well as the generalized HOT Traces and mean diffusivities. M3(b), M4(b), and M6(b) can be linearly combined to achieve the desired isotropic mADC-weighting for a wide range of b-values (Fig.2).