Synopsis

We develop a general framework for estimating orientational and microstructural parameters of neurites. By employing a set of rotational invariants, we analytically reveal the nontrivial topology of the parameter estimation landscape, showing that multiple branches of parameters describe the measurement almost equally well, with only one of them corresponding to the biophysical reality. A comprehensive acquisition shows that the branch choice differs for white and for gray matter. We reveal hidden degeneracies in MRI parameter estimation for neuronal tissue, provide microstructural and orientational maps in the whole brain without constraints or priors, and assess commonly used parameter constraints.

Purpose

$$$\bullet$$$ To estimate compartment diffusivities, water fractions, and fiber orientation dispersion of axons and dendrites in the whole brain without constraints or priors;

$$$\bullet$$$ To reveal hidden degeneracies affecting accuracy and precision in microstructural parameter estimation;

$$$\bullet$$$ To resolve the degeneracies by acquiring human data up to $$$b\leq10\,$$$ms/μm².

Theory

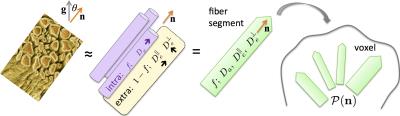
Consider the general picture of anisotropic Gaussian compartments, Fig.1, an overarching model of diffusion at long (clinical) diffusion times. Previous models^[1-9] follow as special cases. The dMRI signal in direction $$${\bf g}$$$ parameterized by diffusion weighting $$$b=q^2t$$$ is a convolution^[4,10-12] on a unit sphere $$$|{\bf n}|=1$$$

$$S_{\bf g}(b)=S(0)\cdot\int_{{\bf n}=1}d{\bf n}\,{\cal P}({\bf n})\,{\cal K}(b,{\bf g\!\cdot\!n})\quad(1)$$

between the fiber ODF $$${\cal P}({\bf n})$$$ and the anisotropic response

$${\cal K}(b,\xi;\,x)=fe^{-bD_a\xi^2}+(1-f)e^{-bD_e^\perp-b(D_e^\parallel-D_e^\perp)\xi^2},\quad\xi={\bf g\!\cdot\!n}\quad(2)$$

of an individual fiber fascicle, Fig.1. Kernel (2) can further include a 3rd (CSF) compartment.

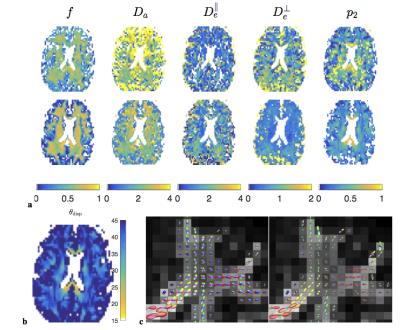
The scalar parameters $$$x=\{f,D_a,D_e^\parallel,D_e^\perp\}$$$, and ODF $$${\cal P}(\bf {n})$$$, carry distinct biophysical significance. Voxelwise fiber ODF provides an adequate starting point for tractography. Scalar parameters make dMRI specific to demyelination ($$$D_e^\perp$$$), axonal loss ($$$f$$$), beading, oedema and inflammation ($$$D_a,D_e^\parallel$$$). Since pathophysiological origins of these values are unknown, ideally, to become specific to pathology, one needs to estimate $$$f,D_a,D_e^\parallel,D_e^\perp$$$ separately.

Here we estimate all the parameters of problem (1-2) without assumptions on the ODF shape and constraints on $$$x$$$. For that, we first factorize Eq.(1) in the spherical harmonics (SH) basis^[4]:

$$S_{lm}(b,x)=p_{lm}\,K_l(b,x).\quad(3)$$

Here $$$S_{lm}$$$ and $$$p_{lm}$$$ are signal and ODF SH coefficients, and $$$K_l(b,x)$$$ are projections of the kernel (2) onto Legendre polynomials^[4,11,12].

In terms of basis-independent rotational invariants^[11,12] of signal and ODF,

$$S_l^2=\sum_{m=-l}^l |S_{lm}|^2/4\pi(2l+1),\quad p_l^2=\sum_{m=-l}^l |p_{lm}|^2/4\pi(2l+1),\quad(4)$$

one per each SH set $$$l$$$, ODF factors out^[10-12]:

$$S_l(b,x)=p_l\,K_l(b,x)\,,\quad l=0,\ 2,\ \dots.\quad(5)$$

Here, $$$p_0\equiv1$$$ (normalization); $$$0\leq\,p_2\leq1$$$ is a "nonlinear FA" of fibers, etc.

Solutions to the system (5) by any means $$$-$$$ using Taylor-expansion in b (LEMONADE^[10]), nonlinear fitting^[11] by minimizing

$$F(x)\propto\sum_{l=0}^L\sum_{b{\rm-shells}}(S_l-p_l\,K_l)^2,\quad(6)$$

or Bayesian estimation^[12] $$$-$$$ are degenerate^[7,10,13]. Degeneracies originate due to multi-compartmental diffusion described by the kernel (2).

Below we investigate the degeneracies and attempt to resolve them using an extensive acquisition.

Experiment

Results

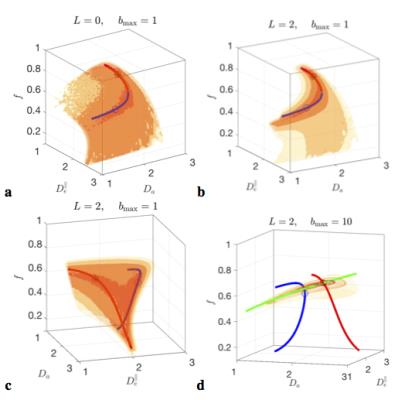
The minimization landscape, Fig.2, of problem (5) has nontrivial topology, depending on the number $$$l=0,2,\dots$$$ of rotational invariants employed:

$$$\bullet$$$ The $$$l=0$$$ invariant alone, $$$S_0=K_0$$$, is equivalent to powder averaging^[14](spherical mean, SMT^[15,16]). Up to $$${\cal\,O}(b^2)$$$, SMT topology is a 2d surface, Fig.2a; hence, for clinical acquisitions, almost perfectly described by DKI, SMT cannot be employed without at least 2 constraints.

$$$\bullet$$$ At the "clinical" level $$${\cal\,O}(b^2)$$$, including the $$$K_2(b)$$$ invariant adds one extra ODF anisotropy parameter $$$p_2$$$ and turns the surface into two narrow 1d trenches, Fig.2b,c. The trenches $$$x_\zeta(p_2)$$$, labeled by index $$$\zeta=\pm$$$, exactly follow as the two "LEMONADE" branches of a quadratic equation that involves rotationally invariant combinations of signal’s diffusion and kurtosis tensors^[10,11]. Physically, 2 branches come from having at least two tissue compartments. We emphasize that both sets of values can look perfectly plausible (Fig.3), and the “wrong” set corresponds to swapping intra- and extra-neurite parameters— which carries the danger of misrepresenting parameter changes in pathology. Including the $$$K_{l>2}(b)$$$ invariants, practically, does not improve precision.

Hence, if acquisition is only sensitive to $$${\cal\,O}(b^2)$$$, due to e.g. b-range or SNR limitations, the parameter estimation problem is “doubly degenerate” [10,13]: with respect to selecting the trench, and due to the perfect flatness of either trench. This degeneracy and flatness are general “hidden” features of problem (1)-(2) for any ODF.

Fig.3 shows that histograms of fit outputs, initialized from 2 low-b LEMONADE branches, remain bimodal even for very high b. Hence, branch choice is a "topological invariant", depending on ground truth values in each voxel.

Using acquisition up to $$$b\leq10\,$$$ms/μm², and employing prevalence method (using 100 random fit initializations/voxel and selecting largest cluster), we see that branch choice is different in WM and in GM (Fig.3).

Fig.4 shows the resulting parameter maps and ODFs.

Discussion and Conclusions

$$$\bullet$$$ Robust parameter estimation for "clinical" dMRI, well-described by $$${\cal\,O}(b^2)$$$ expansion (DKI), is generally impossible without constraints;

$$$\bullet$$$ We are unaware of justifiable parameter constraints; currently employed constraints^[8,15,16] generally do not hold, Fig.5, introducing spurious correlations and bias into estimated parameter values;

$$$\bullet$$$ High-b acquisition shows that scalar parameters vary across brain, and must be separately estimated even in healthy subjects;

$$$\bullet$$$ Clinical studies should employ "orthogonal" measurements^[17-20], e.g. isotropic weighting, for obtaining interpretable microstructural trends.

Acknowledgements

References

1. Behrens et al., Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging, Nat Neurosci 6, 750 (2003)

2. Kroenke et al., On the Nature of the NAA Diffusion Attenuated MR Signal in the Central Nervous System, MRM 52, 1052 (2004)

3. Assaf et al., New Modeling and Experimental Framework to Characterize Hindered and Restricted Water Diffusion in Brain White Matter, MRM 52, 965 (2004)

4. Jespersen et al., Modeling dendrite density from magnetic resonance diffusion measurements, NeuroImage 34, 1473 (2007)

5. Jespersen et al., Neurite density from magnetic resonance diffusion measurements at ultrahigh field: Comparison with light microscopy and electron microscopy, NeuroImage 49, 205 (2010)

6. Fieremans et al., Monte Carlo study of a two-compartment exchange model of diffusion, NMR Biomed 23, 711 (2010)

7. Fieremans et al., White matter characterization with diffusional kurtosis imaging, NeuroImage 58, 177 (2011)

8. Zhang et al., NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain, NeuroImage 61, 1000 (2012)

9. Sotiropoulos et al., Ball and rackets: Inferring fiber fanning from diffusion-weighted MRI, NeuroImage 60, 1412 (2012)

10. Novikov et al., From diffusion signal moments to neurite diffusivities, volume fraction and orientation distribution: An exact solution, Proc ISMRM 2015, p. 469

11. For mode details, see unpublished preprint: Novikov et al., Mapping orientational and microstructural metrics of neuronal integrity with in vivo diffusion MRI, https://arxiv.org/abs/1609.09144

12. Reisert et al., Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach, NeuroImage, DOI:10.1016/j.neuroimage.2016.09.058

13. Jelescu et al., Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue, NMR Biomed 29, 33 (2016)

14. Jespersen et al., Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments, NMR Biomed 26, 1647 (2013)

15. Kaden et al., Quantitative Mapping of the Per-Axon Diffusion Coefficients in Brain White Matter, MRM 75, 1752 (2016)

16. Kaden et al., Multi-compartment microscopic diffusion imaging, NeuroImage 139, 346 (2016)

17. Szczepankiewicz et al., Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors, NeuroImage 104, 241 (2015)

18. Dhital et al., Isotropic Diffusion Weighting Provides Insight on Diffusion Compartments in Human Brain White Matter In vivo, Proc. ISMRM, p.2788 (2015)

19. Szczepankiewicz et al., The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE), NeuroImage DOI:10.1016/j.neuroimage.2016.07.038 (2016)

20. Skinner et al., Rapid In Vivo Detection of Rat Spinal Cord Injury with Double-Diffusion-Encoded Magnetic Resonance Spectroscopy, MRM DOI:10.1002/mrm.26243 (2016)