Introduction

In order to extract more specific microstructural information from MRI without model assumptions, measurements reflecting more flavors of the underlying tissue are needed. One such technique in diffusion MRI is multi-dimensional diffusion encodings that have recently gained interest due the possibility of measuring the microscopic fractional anisotropy (µFA), which, unlike a conventional FA measurement, is insensitive to dispersion^1,2. One approach for this measurement combines the conventional linear tensor encoding (LTE) with spherical tensor encoding (STE) performed by the magic angle spinning of the q-vector (q-MAS) method. The original approach assumes that the measured diffusion spectra are constant, which may lead to a µFA bias in systems exhibiting time-dependent diffusion^3,4. To correct for this bias and at the same time probe the time-dependency of diffusion, which reflects the length scales of the underlying microstructure, we propose the combination of spectrally modulated schemes sensitive to different time scales. We experimentally demonstrate the method on phantoms with well-known microstructures and post-mortem neuronal tissue.

Theory

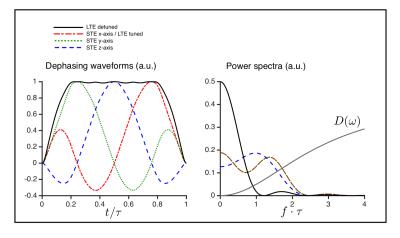
The power spectrum of the diffusion encoding describes the sensitivity filter for the diffusion spectrum (D(ω)), which is non-constant for time dependent diffusion (Fig. 1) ⁵. The optimised STE⁶ have sufficiently similar spectral content in the individual axes to reflect the same diffusion times. An LTE with similar, i.e. tuned, spectral content can be realized as a projection of one of the STE axes. A detuned LTE with more encoding power at lower frequencies is obtained from the magnitude of the STE gradient trajectory (compare solid and broken lines in Fig. 1).

Methods

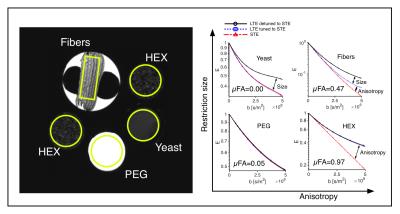
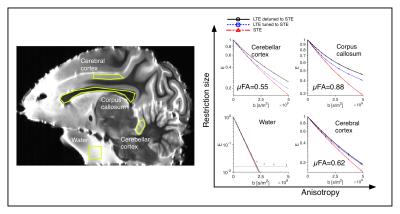
Phantoms and tissue: Four diffusion phantoms were designed to yield specific diffusion characteristcs: i) isotropic multicomponent Gaussian diffusion was constructed by the use of PEG (Polyethylene glycol) mixed with water⁷ ii) a two-compartment system with isotropic and restricted diffusion by a yeast cell suspension¹ iii) a system with time-independent microscopic anisotropy but complete orientation dispersion by the use of a liquid crystal forming a hexagonal array of water channels (HEX) with 7 nm diameter⁸ and iv) a system with time-dependent anisotropic diffusion by the use of hollow electrospun fibers with mean diameter of 13.4 µm ⁹. An excised brain from a 3.5 year old vervet monkey was prepared for ex vivo imaging¹⁰. The live animal was handled following the ethical guidelines of the local ethics committee on St Kitts. Experiments and analysis: Experiments were performed on a preclinical 4.7 T Agilent MRI scanner with a quadrature coil. Three different gradient waveforms were used: an optimized STE⁶, a tuned LTE from the x-projection of the STE scaled by $$$\sqrt{3}$$$ and a detuned LTE from the magnitude of the STE. Pairs of 23 ms long encoding gradients were applied with 15 uniformly distributed directions and 12 b-values between 200 and 4800 s/mm² using a maximum gradient amplitude of 500 mT/m. Image resolution was 0.375x0.375x2 mm³ for the phantom experiment and 0.25x0.25x2 mm³ for the monkey experiment. A 2D spin-echo sequence with TE/TR: 68/2500 ms was used for both experiments. Total acquisition time was 96 hours. The powder averaged signals over ROIs were fitted to 3^rd order in b and the µFA was calculated based on the tuned LTE and STE data¹.

Results and Discussion

All four phantoms showed qualitatively different powder-averaged signal attenuations, with a higher variance with LTE relative to STE in anisotropic media and with contrast between the tuned and detuned LTE in time dependent domains (Fig. 2). The signals from ROIs in the monkey brain also demonstrate anisotropy to different degrees and time dependence in the corpus callosum and in an ROI in the cerebellar cortex (Fig. 3), qualitatively matching the findings from the hollow electrospun fibers (Fig. 2). The cerebellar cortex contains densely packed large neurons in the granular layer and has shown large frequency dependence in earlier OGSE studies¹¹. The cerebral cortex ROI is anisotropic with negligible time dependence, qualitatively similar to the HEX phantom, presumably due to a main µFA contribution from thin dendrites. Simulations confirmed sensitivity to time-dependence in a range of realistic cellular geometries (data not shown).

Conclusion

We propose spectrally tuned and detuned combinations of STE and LTE to probe µFA and time-dependent diffusion in one experimentally feasible imaging framework. We experimentally demonstrate the method on phantoms with well-known microstructures, providing technical validation of the approach. Results from a fixed monkey brain further illustrate the method’s potential to extract microstructurally specific parameters from neuronal tissue directly from data without model assumptions. This gives new opportunities for improved tissue characterization and validation of model parameters.

Acknowledgements

This project was supported by Vinnova, VINNMER Marie Curie Industry Outgoing (2013-04350). Henrik Lundell is supported by the Danish Council for Independent Research (4093-00280A and 4093-00280B). The design of the electrospun fibre phantom was supported by the CONNECT network supported by the Future and Emerging Technologies (FET) programme within the Seventh Framework Program for Research of the European Commission, under FET-Open (23829) .