1037
Wave-LORAKS for faster Wave-CAIPI MRI1Electrical Engineering, University of Southern California, Los Angeles, CA, United States, 2A. A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Radiology, Harvard Medical School, Charlestown, MA, United States, 4Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany
Synopsis
Wave-CAIPI is a novel technique that enables accelerated acquisition with negligible g-factor penalty by using corkscrew readout trajectories, while LORAKS (LOw-RAnk modeling of local K-Space neighborhoods) is a powerful approach to constrained reconstruction that integrates sparse support, phase, and parallel imaging constraints into a unified linear prediction framework. In this work, we propose a new fast imaging technique called Wave-LORAKS, which combines Wave-CAIPI acquisition with LORAKS-based reconstruction. Retrospective undersampling experiments with 3D T1-weighted data show that Wave-LORAKS enables higher acceleration and more flexible sampling compared to traditional Wave-CAIPI, allowing up to 15-fold acceleration with similar quality as 9-fold accelerated Wave-CAIPI.
Purpose
We introduce a novel fast imaging approach called Wave-LORAKS, which combines the advantages of two powerful and complementary fast imaging techniques: Wave-CAIPI1 data acquisition and LORAKS2 reconstruction.
Wave-CAIPI is a recent data acquisition technique that enables high acceleration factors with minimal g-factor penalty. Wave-CAIPI is based on Controlled Aliasing In Parallel Imaging (CAIPI) 3 undersampling, but employs additional corkscrew-shaped readout trajectories to achieve more efficient spatial encoding. Traditional Wave-CAIPI reconstruction solves a simple linear least-squares problem in the style of SENSE4. While Wave-CAIPI has been very successful, there is substantial interest in accelerating Wave-CAIPI even further using advanced constrained reconstruction techniques. For example, Curtis et al.5 and Bilgic et al.6 proposed compressed sensing (CS) based reconstruction for Wave-CAIPI, enabling higher acceleration factors using variable-density Poisson disc sampling and $$$\ell_1$$$-regularized reconstruction. In this work, we explore the combination of LOw-RAnk modeling of local K-Space neighborhoods (LORAKS) 2 with Wave-CAIPI acquisition.
LORAKS is a powerful and flexible constrained reconstruction framework, that integrates sparse support, phase, and parallel imaging constraints into a unified formulation based on linear-prediction relationships and low-rank matrix recovery2,7-10. LORAKS has previously been shown to enable a substantially higher flexibility in the choice of sampling scheme and better reconstruction performance relative to other popular advanced reconstruction methods.
Methods
The Wave-LORAKS optimization problem is formulated as
$$$ \arg\min_\boldsymbol{\rho} \vert \vert \mathbf{E}\boldsymbol{\rho} – \mathbf{k} \vert \vert ^2 + \lambda ({J}_x(\boldsymbol{\rho}) + {J}_y(\boldsymbol{\rho}) + {J}_z(\boldsymbol{\rho}))$$$,
where $$$\mathbf{E}$$$ is the matrix modeling the Wave-CAIPI data acquisition, including weighting by the coil sensitivity maps and Fourier sampling along corkscrew trajectories; $$$\boldsymbol{\rho}$$$ is the image to be reconstructed; $$$\mathbf{k}$$$ is the measured k-space data; $$$\lambda$$$ is a regularization parameter; and the $$$ {J}(\cdot)$$$ terms are regularization penalties that encourage LORAKS matrices to have low-rank . The first term in this equation is the standard Wave-CAIPI data consistency constraint, while the remaining three terms are associated with LORAKS regularization. While LORAKS constraints could be formulated in 3D, we instead use 2D LORAKS by summing over every 2D data slice for all 3 orientations ($$$x,y,z$$$). The 2D formulation leads to substantial memory savings.
For faster computation speed, we use the AC-LORAKS10 technique, in which the null-space of the LORAKS matrix is estimated a priori from training data. This simplifies the LORAKS reconstruction from a nonlinear nonconvex low-rank matrix recovery problem into a simple linear least squares problem. In this abstract, we estimate the null-space from an initial Wave-CAIPI reconstruction of the same accelerated Wave data.
Results
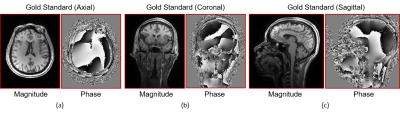
Fully sampled 3D MPRAGE data was acquired on a 3T scanner with Wave encoding as shown in Fig. 1. The data was acquired with a 32-channel array, which was coil compressed down to 16 channels. This data was then retrospectively undersampled using different sampling strategies and reconstructed using Wave-LORAKS.
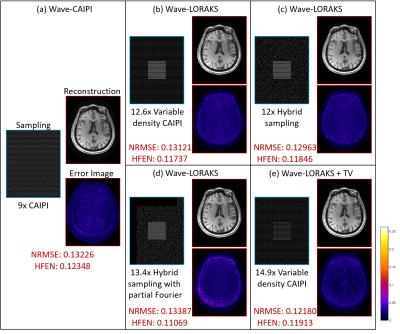
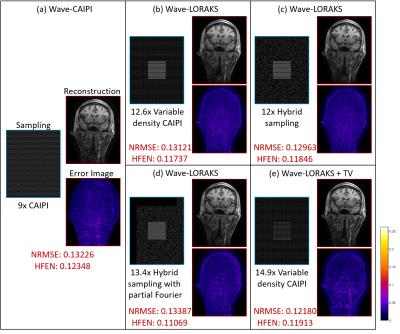
Figs. 2, 3, and 4(a)-(d) show the reconstruction results of Wave-CAIPI and Wave-LORAKS using various sampling patterns. The results show that Wave-LORAKS enables higher acceleration factors than traditional Wave-CAIPI with lower normalized root mean-squared error (NRMSE) and lower high frequency error norm (HFEN) 11 (i.e., the NRMSE of the high-pass filtered image), demonstrating that Wave-LORAKS enables both higher acceleration factors and more flexible sampling trajectories.
Wave-LORAKS is also easily combined with other constraints, such as sparsity. Figs. 2, 3, and 4(e) show results when Wave-LORAKS is combined with total variation (TV). With 14.9x variable density CAIPI sampling, Wave-LORAKS combined with sparsity constraints has lower NRMSE and lower HFEN than 9x Wave-CAIPI.
Discussion
With our data of size 1440x240x192 and 16 channels, the reconstruction time takes 6.5 hours in Matlab using a simple desktop computer (Intel Xeon E5-1620 3.7 GHz quad core CPU processor and 64GB memory). For reference, with the same computer and Matlab implementation, conjugate gradient based Wave-CAIPI takes 45 minutes, and an ADMM implementation of Wave-CS6 takes 3 hours. Currently, we have not yet optimized for the reconstruction speed, but it can be improved dramatically by using faster hardware and better algorithms. Faster implementation is an interesting topic for further exploration.Conclusion
This work introduced and evaluated the new Wave-LORAKS approach for highly accelerated MRI. Our experimental results indicate that Wave-LORAKS is quite powerful relative to standard Wave-CAIPI. Specifically, the Wave-CAIPI acquisition and LORAKS reconstruction combine synergistically, allowing even higher acceleration factors with higher flexibility in the choice of sampling trajectories. While this work focused on 3D Wave-CAIPI acquisition, the extension of Wave-LORAKS to simultaneous multi-slice (SMS) acquisition (Wave-SMS) 12 would also be straightforward.Acknowledgements
This work was supported in part by Annenberg Fellowship, Kwanjeong Educational Foundation Scholarship, NSF CAREER award CCF-1350563, and NIH research grants R21-EB022951, R01-NS089212, R24-MH106096, P41-EB015896, and R01-EB020613.
References
1. Bilgic B, Gagoski B, Cauley S, Fan AP, Polimeni J, Grant P, Wald L, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn Reson Med 2015;73:2152–2162.
2. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imag 2014;33:668–681.
3. Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med 2006;55:549–56.
4. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-962.
5. Curtis AT, Bilgic B, Setsompop K, Menon RS, Anand CK. Wave-CS: combining wave encoding and compressed sensing. ISMRM, Canada, 2015, p.82.
6. Bilgic B, Ye H, Wald LL, Setsompop K. Optimized CS-Wave imaging with tailored sampling and efficient reconstruction. ISMRM, Singapore, 2016, p.612.
7. Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med 2016;75:1499–1514.
8. Haldar JP. Low-rank modeling of local k-space neighborhoods: from phase and support constraints to structured sparsity. Proc SPIE 2015;9597:959710.
9. Kim TH, Setsompop K, Haldar JP. LORAKS makes better SENSE: phase-constrained partial Fourier SENSE reconstruction without phase calibration. Magn Reson Med 2016, doi:10.1002/mrm.26182.
10. Haldar JP. Autocalibrated LORAKS for Fast Constrained MRI Reconstruction. IEEE International Symposium on Biomedical Imaging: From Nano to Macro, New York City, 2015, pp. 910-913.
11. Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans Med Imag 2011;30:1028–1041.
12. Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL,Setsompop K. RARE/turbo spin echo imaging with simultaneous multislice Wave-CAIPI. Magn Reson Med 2015;73:929–938.
Figures