0973
Using non-linear tissue biomechanics to infer static forces within tissue: towards quantifying IFP1Division of Imaging Sciences and Biomedical Engineering, King’s College London, London, United Kingdom
Synopsis
Quantifying static forces in the context of oncology, such as interstitial fluid pressure, would represent a valuable biomarker in therapy monitoring. Nonlinear tissue mechanics leads to distinct signatures of apparent anisotropic changes in mechanical shear properties in the vicinity of an object that exerts pressure onto its surroundings. Tissue nonlinearity can be modelled for instance via hyper elasticity. We show that the apparent modulation in tissue stiffness can be accounted for when incorporating the nonlinear anisotropic model into the estimation of the biomechanics via MR-Elastography. Knowledge of the deformation tensor enables direct quantification of underlying static forces, hence pressure.
Introduction
Primary tumour forces – such as tumour Interstitial Fluid Pressure (IFP) and cell traction force at the tumour border zone – are thought to be key indicators of therapy response and metastatic potential. While IFP is an accepted biomarker for therapy planning and evaluating treatment efficacy1, its non-invasive measurement remains an elusive target in oncology2. Nonlinear tissue mechanics leads to distinct signatures of apparent anisotropic changes in mechanical shear properties in the vicinity of an object exerting pressure onto its surroundings. Our aims are to demonstrate a) that an inflated spherical object inside tissue generates distinct patterns of apparent stiffness changes and b) that knowledge of the initial deformation field allows accounting for those unique alterations. Identification of this deformation field enables direct quantification of underlying static forces, hence pressure.Methods
Nonlinear elasticity theory
The constitutive properties of a soft tissue under static load can be modelled using a hyperelastic formulation. Here we assume an incompressible neo-Hookean material, for which the elastic modulus can be evaluated analytically:
$$ \mathcal{C}_{ijml}=\frac{\mu_{10}}{J}\left[ B_{lj}\delta_{im}-\frac{2}{3}(B_{ij}\delta_{ml}+B_{ml}\delta_{ij}) + \delta_{ml}\delta_{ij}\left( \frac{2I_\mathbf{B}}{9}+\frac{pJ}{\mu_{10}}\right) + \delta_{mj}\delta_{il}\left( \frac{I_\mathbf{B}}{3}+\frac{pJ}{\mu_{10}}\right) \right] \qquad (\mathbf{eq1})$$
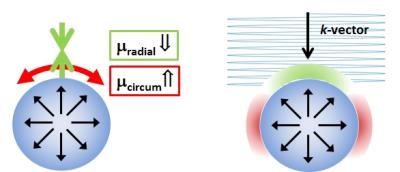
The terms F, p, J, and IB denote the deformation gradient, hydrostatic pressure, Jacobian and the first invariant of $$$ \mathbf{B}=J^{-2/3}\mathbf{FF}^T$$$ respectively. μ10 represents the stiffness parameter of the material. In the vicinity of an inflated spherical object, the material will be radially compressed, and circumferentially stretched leading to apparent transverse isotropic properties around the surface. The solution of the Christoffel equation shows that the apparent stiffness is decreased near the leading edge of the sphere, and increased on the sides (Fig.1).
Sample measurements
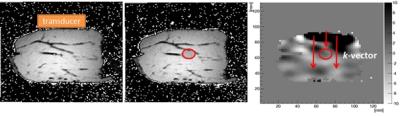
A 5Fr pulmonary balloon catheter was inserted into a bovine tissue specimen (Fig.2). MRE3 and high resolution T2-weighted anatomical images were acquired on a clinical 3T MR scanner (Achieva, Philips Healthcare, The Netherlands). Data acquisition was performed prior to, and after balloon inflation. The deformation gradient F was extracted from the anatomical images using SimpleElastix4.
Results
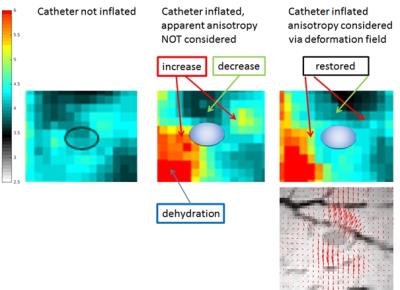
The baseline and the inflated MRE datasets were initially reconstructed under the assumption of isotropic tissue properties, providing maps of shear speed (Fig.3). The moduli estimated in this way for the inflated case are apparent quantities based on the application of the linear wave equation. The predicted decrease in apparent stiffness near the leading edge of the sphere and the corresponding increase on the sides are clearly visible. Those effects however originate in the non-linear regime from the macroscopic deformation F. Thus, knowing F, it is possible to isolate the geometric contribution from the underlying parameter μ10 that remains fixed between deformation states. The elastic wave equation, in conjunction with (eq1), was then used to yield an adjusted modulus map which incorporated the deformation information (Fig.3). The adjusted map returns the previously increased/decreased elasticities back to their original values in the vicinity of the balloon. Knowledge of F and μ10 allows to estimate the pressure within the object via $$$ p = -\sigma_{RR}$$$ where $$$\mathbf{\sigma} = \frac{1}{J}\mathbf{PF}^T$$$ (P: first Piola-Kirchoff Stress).Conclusion
We have presented a proof-of-concept for determining static forces using MRE in conjunction with image registration and nonlinear mechanics theory. Knowledge of the initial deformation state will be absent in a clinical setting of a developed tumour. We hypothesise that multiple acquisitions at different macroscopic deformation states will allow inference of the initial deformation field and, subsequently, the interstitial fluid pressure.Acknowledgements
This work was funded by the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039References
[1] Munson, J. M. & Shieh, A. C. Interstitial fluid flow in cancer: implications for disease progression and treatment. Cancer management and research 6, 317-328, doi:10.2147/CMAR.S65444 (2014).
[2] Heldin, C. H., Rubin, K., Pietras, K. & Ostman, A. High interstitial fluid pressure - an obstacle in cancer therapy. Nature reviews. Cancer 4, 806-813, doi:10.1038/nrc1456 (2004).
[3] Garteiser, P. et al. Rapid acquisition of multifrequency, multislice and multidirectional MR elastography data with a fractionally encoded gradient echo sequence. NMR in biomedicine 26, 1326-1335, doi:10.1002/nbm.2958 (2013).
[4] Kasper Marstal, Floris Berendsen, Marius Staring, et al. SimpleElastix: A user-friendly, multi-lingual library for medical image registration. International Workshop on Biomedical Image Registration (WBIR), Las Vegas, Nevada, USA, 2016.
Figures