0962
Real-time B0 concomitant field compensation for a compact 3T MR scanner with asymmetric transverse gradients1Radiology, Mayo Clinic, Rochester, MN, United States, 2GE Healthcare, Waukesha, WI, United States, 3MRI, GE Global Research, Niskayuna, NY, United States
Synopsis
A prototype, high-performance gradient system capable of 80 mT/m and 700 T/m/s with asymmetric design has been installed. Zeroth-order concomitant field terms endemic to MRI systems employing asymmetric gradient designs cause blurring and ghosting in spiral scans, as well as image quality degradation in fast-spin-echo imaging. The theory is reviewed, and a real-time hardware compensation is demonstrated to correct for the effect.
Purpose
Magnetic resonance imaging (MRI) relies on the use of linear magnetic field gradients for spatial localization. Assumptions involving the ideality of these imaging gradients are the source of a variety of artifacts in MRI. One non-ideality is the Maxwell or concomitant field terms[1]. These time-varying magnetic field terms are temporally coupled with gradient activity. Whole-body MR systems with gradient coils employing cylindrical symmetry exhibit concomitant field leading terms with quadratic spatial dependence. Several correction methods have been developed to correct their effect[1–5]. Recently a lightweight, compact 3T MRI system employing asymmetric transverse gradients has been developed[6–9]. The asymmetry of the transverse gradient axes leads to two additional concomitant field terms, linear and zeroth-order (B0) terms[10]. Previous work has demonstrated a pre-emphasis method[11] to correct for the linear concomitant field term in real-time. This work will demonstrate the efficacy of a hardware compensation for the zeroth-order or B0 term, and compare it to a software correction.Theory
Concomitant field terms can be calculated from considering the net magnetic field as a function of time and location:$$|\mathbf{B}(x,y,z,t)|\approx B_{0}+G_{x}(t)x+G_{y}(t)y+G_{z}(t)z+B_{c}(x,y,z,t) Eq (1)$$.
The linear gradient terms represent the ideal applied gradients, while Bc contains undesired terms. Bc can be expanded[10,11] to show the 0th, 1st, and 2nd order terms. The zeroth order term,$$B_{c,0th}(t) = \frac{z_0^2(G_x^2(t)+G_y^2(t))}{2B_0} Eq (2)$$is the focus of this work, where z0 is the offset of the transverse (asymmetric) gradients from the magnet isocenter. The center frequency of an MR experiment is set as $$$f_{0}(t)=\frac{\gamma}{2\pi}B_{0}$$$ the additional constant off-resonance from the zeroth order concomitant field can be compensated for by applying a frequency shift $$$\Delta f_{c,0th}(t)$$$, such that $$f_{corrected}(t)=f_0+\Delta f_{c,0th}(t)=\frac{\gamma}{2\pi}B_{0}+\frac{\gamma}{2\pi}\frac{z_0^2(G_x^2(t)+G_y^2(t))}{2B_0} Eq (3)$$.
Methods
The zeroth order concomitant field correction was implemented onto the system board responsible for zeroth order eddy current correction[12], and takes as input the two asymmetric transverse gradient values and applies a the frequency shift to RF transmit and receive in real-time according to Equation 3.
All scans were acquired on a lightweight, low-cryogen prototype MR system (GE Global Research, Niskayuna, NY) equipped with asymmetric gradients capable of 80 mT/m and 700 T/m/s. A spiral acquisition with 4096 readout points, 16 arms, 5 mm slice thickness, ±125 kHz receiver bandwidth and a 12 cm FOV was acquired at isocenter on the American College of Radiology (ACR) musculoskeletal phantom (MSK). A two-shot gradient-echo B0 mapping sequence was also acquired, employing a 256×256 matrix, ±15.63 kHz readout bandwith, and 1 ms echo time difference. The spiral scans were acquired with and without the B0 concomitant field compensation, and all gradient waveforms were retained to apply the accumulated phase to each data point based on Eq. 2. as the software correction. The spiral reconstruction utilized a non-iterative type-III non-uniform fast Fourier transform (NUFFT) implemented with a 1.5x oversampled FFT operator and 5-point Kaiser-Bessel window. This reconstruction accounted for off-resonance and gradient nonlinearity effects. The off-resonance was corrected based on time-segmentation (N = 16) [13], and the second-order concomitant field was also corrected[4].
A sagittal T2 weighted fast spin echo series on a human volunteer under an IRB approved protocol was acquired: TR = 5000 ms, TE = 116 ms, 4 mm slice thickness, 512×384 acquisition matrix with a 22 cm FOV, ±62.5 kHz receiver bandwidth, partial Fourier sampling and an echo train length of 16. The hardware B0 concomitant field compensation was switched on and off.
Results
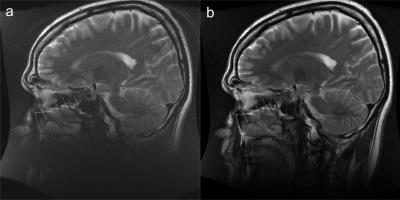
Figure 1 shows the spiral acquisition reconstructed with (a) no B0 correction, (b) a reconstruction-based B0 correction, and (c) the proposed hardware B0 correction. Figure 1b and 1c agree closely and show that the blurring effect due to 0th order concomitant field is eliminated. Figure 2 shows a sagittal T2-weighted FSE image without (a) and with (b) the B0 concomitant field correction.Discussion
Correction of the B0 concomitant field term is necessary for successful imaging in a system with asymmetric gradient axes. While a software correction could be implemented, it would require extensive modification to the pulse sequence and reconstruction environment, as each and every sequence and reconstruction pair would have to store gradient waveforms for every acquisition. Additionally, the correction would then not be applied to any off-resonance effects during combined RF excitation and gradient activity. The proposed real-time compensation corrects the problem without the need to tailor the software on a per-sequence basis, and therefore is completely transparent to the user.Conclusion
A real-time correction for the B0 concomitant field of a MRI system employing asymmetric transverse gradient systems has been demonstrated to compensate for the effect.Acknowledgements
Funding Support: NIH R01EB010065References
[1] Bernstein MA, Zhou XJ, Polzin JA, King KF, Ganin A, Pelc NJ, et al. Concomitant gradient terms in phase contrast MR: Analysis and correction. Magn Reson Med 1998;39:300–8. doi:10.1002/mrm.1910390218.
[2] Zhou XJ, Tan SG, Bernstein M a. Artifacts induced by concomitant magnetic field in fast spin-echo imaging. Magn Reson Med 1998;40:582–91.
[3] Zhou XJ, Du YP, Bernstein MA, Reynolds HG, Maier JK, Polzin JA. Concomitant magnetic-field-induced artifacts in axial echo planar imaging. Magn Reson Med 1998;39:596–605.
[4] King KF, Ganin A, Zhou XJ, Bernstein MA. Concomitant gradient field effects in spiral scans. Magn Reson Med 1999;41:103–12. doi:10.1002/(SICI)1522-2594(199901)41:1<103::AID-MRM15>3.0.CO;2-M.
[5] Du YP, Joe Zhou X, Bernstein MA. Correction of concomitant magnetic field-induced image artifacts in nonaxial echo-planar imaging. Magn Reson Med 2002;48:509–15. doi:10.1002/mrm.10249.
[6] Lee S, Mathieu J, Piel JE, Hardy CJ, Schenck JF, Tan ET, et al. Brain imaging with a Dedicated Asymmetric Head-only Gradient Coil without Peripheral Nerve Stimulation at 500 T/m/s. ISMRM Annu. Meet., vol. 22, Milan: 2014, p. 310.
[7] Mathieu J-B, Amm BC, Lechner-greite S, Lee S-K, Tan ET, Foo TK-F, et al. Design of High Performance Gradient Coil for 3T Head Specialty Scanner. Proc 20th Annu. Meet. ISMRM, vol. 20, 2012, p. 2588.
[8] Lee S-K, Mathieu J-B, Graziani D, Piel J, Budesheim E, Fiveland E, et al. Peripheral nerve stimulation characteristics of an asymmetric head-only gradient coil compatible with a high-channel-count receiver array. Magn Reson Med 2015:n/a-n/a. doi:10.1002/mrm.26044.
[9] Weavers PT, Shu Y, Tao S, Huston J, Lee S-K, Graziani D, et al. Technical Note: Compact three-tesla magnetic resonance imager with high-performance gradients passes ACR image quality and acoustic noise tests. Med Phys 2016;43:1259–64. doi:10.1118/1.4941362.
[10] Meier C, Zwanger M, Feiweier T, Porter D. Concomitant field terms for asymmetric gradient coils: Consequences for diffusion, flow, and echo-planar imaging. Magn Reson Med 2008;60:128–34. doi:10.1002/mrm.21615.
[11] Tao S, Weavers PT, Trzasko JD, Shu Y, Huston J, Lee S, et al. Gradient pre-emphasis to counteract first-order concomitant fields on asymmetric MRI gradient systems. Magn Reson Med 2016;0. doi:10.1002/mrm.26315.
[12] Crozier S, Eccles CD, Beckey FA, Field J, Doddrell DM. Correction of eddy-current-induced B0 shifts by receiver reference-phase modulation. J Magn Reson 1992;97:661–5. doi:10.1016/0022-2364(92)90049-D.
[13] Noll DC, Meyer CH, Pauly JM, Nishimura DG, Macovski A. A homogeneity correction method for magnetic resonance imaging with time-varying gradients. IEEE Trans Med Imaging 1991;10:629–37. doi:10.1109/42.108599.
Figures