Synopsis

Functional Magnetic Resonance Imaging (fMRI) is a key neuroimaging technique in large cohort studies, allowing the analysis of healthy and pathological networks of spontaneous brain function. However, resting stage fMRI analysis is often limited by the requirement for image registration and the resulting spatial smoothing used to ensure spatial consistency between subjects. We propose an analysis strategy to overcome these limitations using a novel non-linear Sparse Autoencoder to produce functional network decompositions in each subject without the need for spatial smoothing nor registration. This technique applied at both the group and individual level retains the capability to obtain unique single subject functional network representations. We use this technique to reveal consistent individual-level network differences between a group of healthy controls and individuals diagnosed with young-onset dementia; most strikingly in areas representing a working-memory network.

PURPOSE

METHODS

We propose a non-linear Sparse Autoencoder [1,2] with one hidden layer that minimizes the following cost function:$$\min_{W^g,V^g}\frac{1}{2m}||\hat{X}-X||_2^2+\lambda(||\mathbf{W^g}||_2^2+||\mathbf{V^g}||_2^2)+\beta*KL(\rho||\hat{\rho})$$with the sigmoid activation function $$$f:\mathbb R\to \mathbb R$$$ given by $$$f(x)=\frac{1}{1-\exp(-x)}$$$, $$$\mathbf{W^g}$$$ is the weight matrix mapping the data $$$X$$$ into the hidden components $$$h=f(\mathbf{W^g}X+\mathbf{b_1^g})$$$ with $$$\mathbf{W^g} \in \mathbb R^{(k*s)\times k}$$$, $$$\mathbf{V^g}$$$ reconstructs the data $$$\hat{X}=\mathbf{V^g}h+\mathbf{b_2^g}$$$ from the hidden units with $$$\mathbf{V^g} \in \mathbb R^{k \times (k*s)}$$$, $$$\lambda$$$ being the weight decay parameter controlling the relative importance of the regularization term, $$$KL(\rho||\hat{\rho}) = \sum_{j=1}^k \rho\log\frac{\rho}{\hat{\rho_j}} + (1-\rho)\log\frac{1-\rho}{1-\hat{\rho_j}}$$$ is a symmetrized Kullback-Leiber (KL) divergence between a Bernoulli random variable with mean $$$\rho$$$ and a Bernoulli random variable with mean $$$\hat{\rho_j}$$$, and $$$\beta$$$ the relative importance of the sparsity term [1]. A voxel in a hidden component is considered as active if its value is close to 1 or inactive of its value is close to 0. The sparsity parameter $$$\rho$$$ can be understood as the average activation of a hidden component $$$h_j$$$ [1]. The weight matrix $$$\mathbf{W^g}$$$ (and analogously for $$$\mathbf{V^g}$$$) can be seen as a set $$$\mathbf{W^g}=\{\mathbf{W_1^g},...,\mathbf{W_s^g}\}$$$ in which each $$$\mathbf{W_i^g}$$$ is the time course parametrization of each subject $$$i$$$ contributing to the group hidden components. We compute a sparse individual decomposition for each subject $$$i$$$ minimizing the following cost function $$\min_{W_i,V_i}\frac{1}{2m}||\hat{X_i}-X_i||_2^2+\lambda(||\mathbf{W_i}-\mathbf{W_i^g}||_2^2+||\mathbf{V_i^g}-\mathbf{V^g}||_2^2)+\beta*KL(\rho||\hat{\rho})$$with $$$\hat{X_i}=\mathbf{V_i}f(\mathbf{W_i}X_i+\mathbf{b_{1i}})+\mathbf{b_{2i}}$$$. We initialize the parametrization $$$\mathbf{W_i^{init}}$$$ and $$$\mathbf{V_i^{init}}$$$ of each individual subject Autoencoder with its corresponding group parameters $$$\mathbf{W_i^g}$$$ and $$$\mathbf{V_i^g}$$$, respectively. To summarize, we first optimize the group Autoencoding and then proceed to the individual Autoencodings for each subject using the regularization provided by the group time course parametrization as depicted in Figure 1. We compare our proposed method against ICA with Dual Regression [3,4,5].

RESULTS

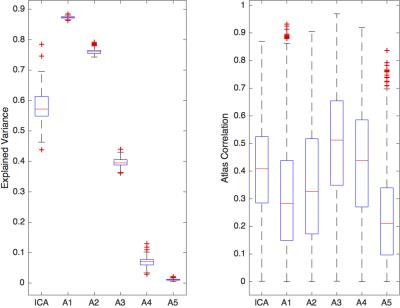
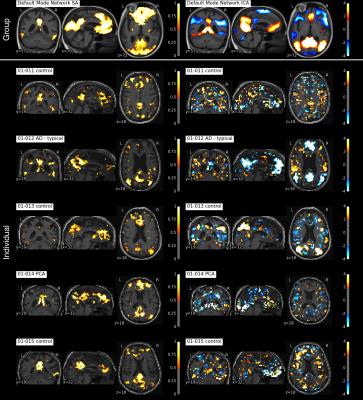
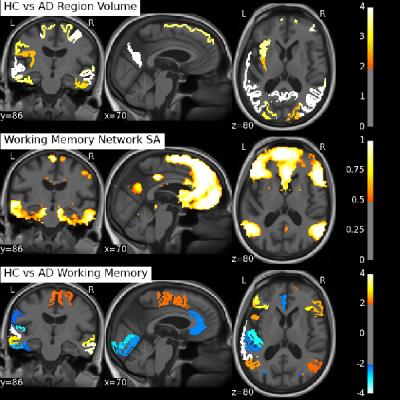
We can either tune our method towards greater reproducibility among subjects or more variance explained in each individual subject as depicted in Figure 2. The following results are presented for $$$\lambda=0.05$$$, for which we achieved the best component reproducibility for all subjects. Both group decomposition techniques produce several previously reported resting-state networks and noticeable noise components which reflect the effect of misregistration (brain edges) and brain pulsatility (white matter and CSF). Figure 3 shows the appearance of the default mode network (DMN) at both group and individual level using the Sparse Autoencoder technique and ICA. The individual Autoencoder decompositions show reduced noise and much stronger spatial coherence than their corresponding ICA counterparts after Dual Regression. The analysis reveals differences in regions associated with working memory in young-onset AD relative to controls depicted in Figure 4, provides evidence that the technique is able to elicit differences relevant to pathology.

DISCUSSION

CONCLUSION

Acknowledgements

References

[1] Bengio, Y., 2009. Learning deep architectures for AI. Foundations and trends® in Machine Learning, 2(1), pp.1-127.

[2] Ng, A., 2011. Sparse autoencoder. CS294A Lecture notes, 72, pp.1-19.

[3] Beckmann, C.F., Mackay, C.E., Filippini, N. and Smith, S.M., 2009. Group comparison of resting-state FMRI data using multi-subject ICA and dual regression. Neuroimage, 47(Suppl 1), p.S148.

[4] Beckmann, C.F. and Smith, S.M., 2004. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE transactions on medical imaging, 23(2), pp.137-152.

[5] Daubechies, I., Roussos, E., Takerkart, S., Benharrosh, M., Golden, C., D'ardenne, K., Richter, W., Cohen, J.D. and Haxby, J., 2009. Independent component analysis for brain fMRI does not select for independence. Proceedings of the National Academy of Sciences, 106(26), pp.10415-10422.

[6] Cardoso et al.Geodesic Information Flows: Spatially-Variant Graphs and Their Application to Segmentation and Fusion. IEEE Trans Med Imaging. 2015 Sep;34(9):1976-88.