0936
On optimizations of MRF patterns based on generalized MRI sequence schemes1Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Institute for Forensic Medicine and Traffic Medicine, University Hospital Heidelberg, Heidelberg, Germany
Synopsis
Within this study, we introduce an MRF pattern generation by the incorporation of a generalized MRI sequence scheme. Optimizations of these patterns lead to a higher matching accuracy and a potential for higher efficiency.
Purpose
Quantitative imaging by magnetic resonance fingerprinting (MRF)1 relies on the distinct signal behavior of dissimilar spin entities under a variation of sequence parameters, a so called MRF pattern. The optimization of such a pattern, in terms of quantification accuracy and efficiency, holds challenges due to the complexity of parameter-space, the ambiguousness of the target function, and focus on one designated MRI imaging sequence. Within this study, we introduce an MRF pattern generation and optimization by the incorporation of a generalized MRI sequence scheme.Methods
A numerical solver for the Bloch equations was developed and implemented in MATLAB (The MathWorks Inc, Natick, Massachusetts, USA) and parallelized for computation on multi-CPU/GPU systems. In general, the effective magnetic field is defined by the RF-elements amplitude, frequency, and phase as well as the gradient-elements absolute amplitude and direction in time. A virtual phantom is characterized as a unique set of the respective proton density (PD) and relaxation times (T1/T2) as well as local field-deviations such as complex RF-modulation and off-resonance. The significance of dephasing effects (gradient spoiling/T2*), slice selection, and spatial encoding are addressed by supersampling.
The optimization of the MRF patterns was performed via a genetic algorithm2. A population of phenotypes (MRF patterns) is ranked within tournament iterations and evolved by genesis (of new), mutation (of preexisting), inheritance (by conjunction at multiple crossover-points) and natural selection (by rank and chance) of phenotypes to minimize the score of a target function. The target function itself was calculated as the weighted sum over the correlation-matrix, to stress distinctness of alike spin entities.
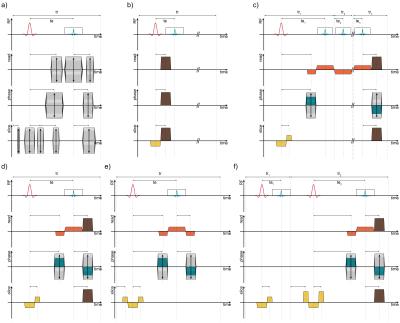
Each phenotype consists of a sequence of various chromosomes (acquisition intervals). In this study, we introduce the use of only one generalized chromosome (cf. 1.a). With each object being fully parameterized independently, different apparent magnetization preparation and imaging techniques such as single- and multi-echo FLASH/FISP, TRUFI or SE are mimicked by the junction of multiple chromosomes (cf. 1).
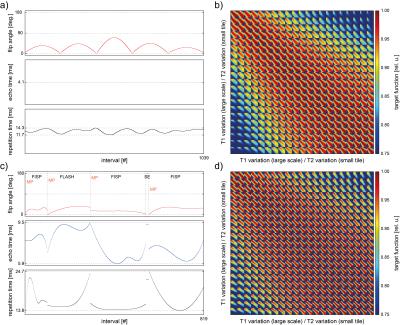
In a preliminary simulation-study, the performance of optimized MRF pattern comprised of segments of inversion-recovery- (IR-), GRE-, FISP-, and SE-imaging techniques with a spline-shaped full degree of freedom in flip angle, RF-phase, echo time (te), and repetition time (tr) was investigated.
Results
Benchmarking of the simulation framework yielded the following complexity estimation: i) direct proportionality in number of time steps and ii) linearity in favor of larger scaled virtual phantoms. The computational overhead for small phantoms and short MRF patterns decreases the acceleration by multi-CPU processing. GPU processing offers an acceleration factor of 100 compared to single CPU computations for reasonably sized phantoms.
The proposed generalization of a sequence scheme offers a new degree of freedom to the generation of MRF pattern and allows for a simple implementation into the sequence code. Optimized MRF patterns result as a composition of different imaging techniques (cf. 2.c,d). Its resulting score of the target function comes out to 0.904 in relative units. A prior presented FISP-MRF pattern3 scores 0.936, respectively (cf. 2.a,b). While the T1 matching quantification degrades for high and low T1 values, the improved accuracy in T2 quantification is denotable (small element of the mosaic view; cf. 2.b,d).
Discussion and Conclusion
Results of this study outline a new design concept for MRF patterns by the implementation of different preparation and imaging techniques. Optimizations of these patterns lead to a higher matching accuracy and a potential for higher efficiency (not investigated within this study). The increase in computational burden to regard for dephasing effects demands for highly-parallelized processing.
The full potential of the introduced generalized MRI sequence scheme is not assessable yet and experimental validation a future topic of research. Minimizing the segment length of each imaging technique may lead to a new perspective of MRF: breaking with using only one designated imaging sequence and allowing for arbitrary signal evolution. This could be one approach to unfold the full potential of magnetic resonance fingerprinting.
Acknowledgements
No acknowledgement found.References
1. Dan Ma, Vikas Gulani, Nicole Seiberlich, et al. Magnetic resonance fingerprinting. Nature. 2013;496:187-192.
2. David E. Goldberg, John H. Holland. Genetic Algorithms and Machine Learning. Machine Learning. 1988;3(2):95–99.
3. Jesse Ian Hamilton, Katherine L Wright, Yun Jiang, et al. Pulse Sequence Optimization for Improved MRF Scan Efficiency. Proc. Intl. Soc. Mag. Reson. Med. 2015;23:3386.
Figures