0935

Motion corrected Magnetic Resonance Fingerprinting using Soft-weighted key-Hole (MRF-McSOHO)

Gastao Cruz¹, René Botnar¹, and Claudia Prieto¹

¹Division of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom

Synopsis

Magnetic Resonance Fingerprinting (MRF) estimates multi-parametric maps from a large amount of highly undersampled time-point images. MRF has been shown to be robust to the presence of abrupt motion occurring towards the end of the acquisition. In this work we further study the effects of different types of motion on MRF, showing high sensitivity to periodic motion and motion occurring at the beginning of the MRF scan. A method for 2D translational motion correction in MRF is proposed and validated in vivo, showing significant improvements when compared with no motion correction.

Introduction

Magnetic Resonance Fingerprinting (MRF)¹ produces multi-parametric maps from a large series of highly undersampled time-point images, via template matching of a measured signal to a set of simulated signals. The original work in¹ demonstrated that MRF still produces accurate parametric maps when a fraction of the time-point images is corrupted by motion. Here, we study the effects of different types of motion during the MRF acquisition and propose a novel approach to correct for this motion (MRF-McSOHO). This method is based on SOft-weighted key-HOle (MRF-SOHO²) reconstruction for highly undersampled MRF data which produces alias free time-point images, enabling motion estimation³ from the reconstructed images. Estimated motion is applied to the motion corrupted k-space, followed by a second MRF-SOHO reconstruction. The proposed approach was validated on standardized T₁/T₂ phantom and in-vivo brain acquisitions.

Methods

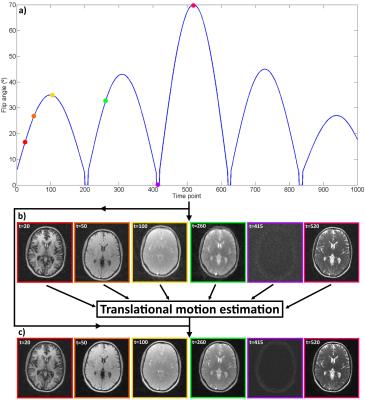
MRF-SOHO combines ideas from parallel imaging⁴, soft-gating⁵ and key-hole⁶ to reconstruct highly undersampled MRF data. The slow varying flip angle in the MRF acquisition produces smooth contrast changes in the time-point images, enabling high frequency data sharing in the temporal dimension. In MRF-SOHO each highly undersampled time-point image I_t is reconstructed by solving I_t = arg min ||W_tⁿ(FSI_t - K_t)||². F is the Fourier transform, S are the coil sensitivities, K_t are the acquired k-space data for time point t and W_tⁿ are the soft-weights for time frame t and neighbour n which control the amount of shared data between time-points. Translational motion for each time-point t is extracted from I_t using image registration. The corresponding phase shifts are applied to produce the motion corrected k-space K'_t. Finally, a second MRF-SOHO reconstruction is performed: I'_t = arg min ||W'_tⁿ(FSI'_t - K'_t)||², producing the motion corrected MRF time series (Figure 1). The MRF dictionary was built with an Extended Phase Graph method based on⁷, using T₁ ranges of [0ms, 6000ms] and [0ms, 1600ms] and T₂ ranges of [0ms, 2600ms] and [0ms, 260ms] for brain and phantom, respectively. Template matching was performed as described in¹.

Experiments

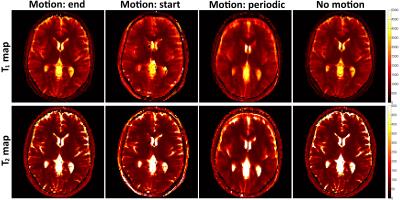
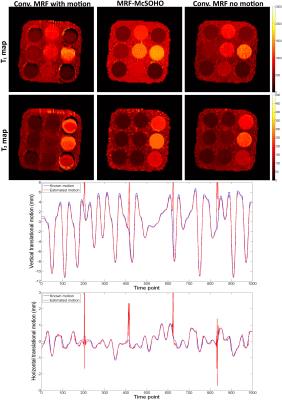
A standardized T₁/T₂ phantom⁶ was scanned in a 1.5T Philips MR scanner using an 18-channel coil. Data was obtained with a rewound gradient echo acquisition after an initial inversion pulse using a tiny golden radial (~23.6º) trajectory⁷. Relevant scan parameters include: resolution 2x2 mm², 10 mm slice thickness, field-of-view 320x320 mm², 8 radial spokes per time-point, 1000 time points and TR (varying between 6.0 and 7.4 ms) and FA (varying between 0º and 70º) patterns similar to the ones described in⁸. One healthy subject underwent a brain scan using a 12-channel coil and the same protocol as above (except field-of-view=440x440 mm²). Three motion experiments were performed by modifying the acquired motion free k-space: 1) abrupt 2D translational motion in the last 100 time-points, 2) abrupt 2D translational motion in the first 100 time-points, 3) realistic 2D respiratory motion throughout all time-points based on previously acquired respiratory signal. The MRF-SOHO neighbourhood size was set to 11 and 21 for the reconstructions before and after motion correction, respectively. All motion experiments were reconstructed with a zero fill gridding reconstruction as in conventional MRF¹ with and without motion, and with the proposed MRF-McSOHO (motion corrected).

Results

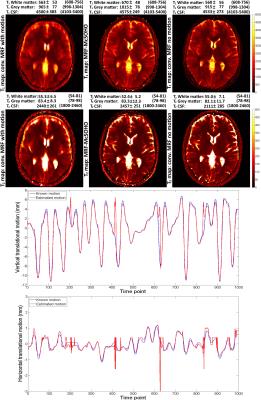
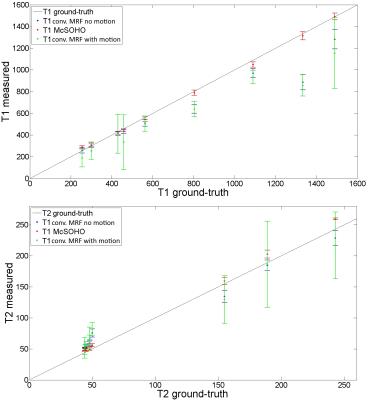
Brain T₁ and T₂ maps for the different type of motions studied are shown in Figure 2 for conventional MRF, demonstrating MRF is robust to motion in the end (as shown in¹), but sensitive to other types of motion. Brain T₁ and T₂ maps and motion estimation plots (in comparison with ground truth) are shown in Figure 3 for conventional MRF and the proposed MRF-McSOHO. Corresponding maps and plots for the phantom dataset can be seen in Figure 4. In both cases artefacts can be seen in conventional MRF in the presence of motion, however these are significantly reduced with the proposed method. 2D reliable motion estimation was obtained for most time-points, except when the flip angle was close to zero. Regardless, no significant artefacts were found in the time-point images or the parametric maps (Figures 3 and 4). T₁ and T₂ measurements of the standardized phantom in comparison to ground-truth values are shown in Figure 5, where MRF-McSOHO achieves higher accuracy and precision than conventional MRF (with and without motion). Additionally, underestimation of high T₁ values was observed for conventional MRF in both datasets, however the proposed method correctly estimated these values.

Conclusion

MRF was shown to be sensitive to periodic motion. A novel method for motion correction in MRF (MRF-McSOHO) was proposed, improving parametric map quality and accuracy. Future work will include further validations in-vivo for different types of motion and different applications.

Acknowledgements

ACKNOWLEGDMENTS: This work was supported by EPSRC EP/P001009/1 and FONDECYT 1161055.

References

1. Ma D et al. Magnetic Resonance Fingerprinting. Nature. 2013; 495:187-192

2. Cruz et al. Accelerated Magnetic Resonance Fingerprinting using Soft-weighted key-Hole (MRF-SOHO). ISMRM. 2017. Submitted

3. Buerger et al. Hierarchical adaptive local affine registration for fast and robust respiratorymotion estimation. Med Image Anal. 2011; 15:551-564

4. Pruessman et al. Advances in sensitivity encoding with arbitrary k-space trajectories. MRM. 2001; 46:638-651

5. Johnson et al. Improved Least Squares MR Image Reconstruction Using Estimates of k-Space Data Consistency. MRM. 2012; 67:1600-1608

6. Song et al. Non-Contrast Enhanced 4-D Dynamic MRA with Golden Angle Radial Acquisition and K-space Weighted Image Contrast (KWIC) Reconstruction. MRM. 2004; 52:815-824

7. Weigel. Extended Phase Graphs: Dephasing, RF Pulses,and Echoes - Pure and Simple. MRM. 2015; 41:266-295

8. Jiang et al. MR Fingerprinting Using Fast Imaging with Steady State Precession (FISP) with Spiral Readout. MRM. 2015; 74:1621-1631

Figures

Figure 1: a) Flip angle used during the acquisition contributes to a smooth change in the magnetization which enables high-frequency data sharing between highly undersampled MRF time-point images (MRF-SOHO reconstruction). Corresponding time-point images are colour coded. b) Initial MRF-SOHO reconstruction of the brain data with realistic 2D pseudo periodic respiratory motion. Time-point images in different motion states are reconstructed with sufficient quality for motion estimation (2D translational motion in this case). c) After motion estimation, the k-space is translation corrected and a second MRF-SOHO reconstruction produces a set of motion corrected time-point images.

Figure 2: T₁ and T₂ maps (in ms) for conventional MRF reconstruction using 3 types of simulated motion: abrupt motion during the last 100 time points (end) of the MRF scan, abrupt motion during the first 100 time points (start) of the MRF scan and realistic respiratory motion throughout all (1000) time points (periodic). MRF is robust to motion at the end of the acquisition, as shown in¹. However, MRF is sensitive to motion when motion occurs at the beginning of the scan, closer to the initial inversion pulse. MRF is also more sensitive to periodic motion throughout the scan.

Figure 3: Top: Brain T₁ and T₂ maps (in ms) for conventional motion corrupted MRF (left), the proposed MRF-McSOHO (middle) and conventional MRF without motion (right). Literature T₁/T₂ values are show in parenthesis. Although no large measurement differences were observed, significant motion artefacts can be seen in T₁ and T₂ maps without motion correction (left), which are reduced with the proposed method (middle), comparable to the no motion case (right). Bottom: plots of the simulated ground-truth 2D periodic motion and estimated motion with MRF-McSOHO. Motion estimation is generally accurate, except for time-points where there is reduced magnetization (low flip angle).

Figure 4: Top: Phantom T₁ and T₂ maps (in ms) for conventional motion corrupted MRF (left), the proposed MRF-McSOHO (middle) and conventional MRF without motion (right). Similarly to Figure 3, motion artefacts propagate into the T₁ and T₂ maps when no motion correction is used (left). The proposed MRF-McSOHO removes most of the motion artefacts, improving quality of the parametric maps. Bottom: plots of the simulated periodic motion and estimated motion with MRF-McSOHO. As in Figure 3, motion is correctly estimated, but tends to fail in time-points where there is little transverse magnetization (corresponding time-points in Figure 1a).

Figure 5: T₁ and T₂ measurement plots (in ms) with conventional motion corrupted MRF (green), conventional MRF without motion (blue) and the proposed MRF-McSOHO, in the presence of 2D respiratory motion (red). Accuracy and precision of both T₁ and T₂ measurements is reduced when no motion correction is applied to conventional MRF. The proposed MRF-McSOHO improves accuracy and precision of all measurements. Additionally, MRF-McSOHO does not underestimate high T₁ (in contrast to conventional MRF in blue), which was also observed in the brain measurements of Figure 3.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0935