Synopsis

The IVIM model and typical DWI-evaluations assume flow in tissue to be incoherent. However, there is evidence that in some tissues flow might be coherent and thus, the DWI-signal might be influenced by the applied first gradient moment m₁. A gradient scheme was implemented that allows applying different m₁ for a constant b-value. Moreover, the IVIM model was extended to also include coherent flow in the modeling process of DWI data. It was found that flow in the human kidney is, at least in part, coherent and that the proposed model is able to fit that data very robustly.

Purpose

Methods

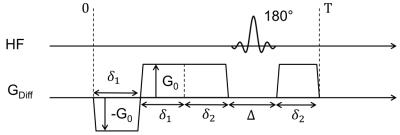
A gradient scheme was implemented that allows to change m₁ while keeping the b-value constant (figure 1). This can be achieved via shortening of δ₁ and prolongation of δ₂ and vice versa. We extended the IVIM model to be able to distinguish between incoherent and coherent flow for high b-values (≥200 s/mm²):

$$S_{b,m_{1}} = S_{0}e^{-b{\underline{\underline{D}}}}[(1-f)-([\beta_{||}cos^{2}(\theta)+\beta_{\bot}sin^{2}(\theta]m_{1}^{2})$$

S_b,m1 is the signal at a certain b-value with a certain m₁. D is the diffusion tensor from which the main direction of diffusion can be derived. f is the fraction of incoherent flow and ϴ the angle between the diffusion gradient and the main direction of diffusion. β_|| and β_⊥ represent the fraction of coherent flow parallel and orthogonal to the main direction of diffusion.

We examined the kidneys of eight healthy volunteers in coronary orientation (FOV 330x330mm², Matrix 140x140, slice thickness 5mm, partial Fourier 6/8, TR 2700ms, TE 89ms, b-Values 0, 250 and 600s/mm²). Every b-value was acquired with 10 different m₁, 2 averages and 20 directions. Values for m₁ were equally distributed between flow compensated (m₁=0) and maximal flow encoding (m₁=m_1,max; achieved at a VENC of 1.4s/mm² (b=250s/mm²) and 0.9s/mm² (b=600s/mm²)).

Results

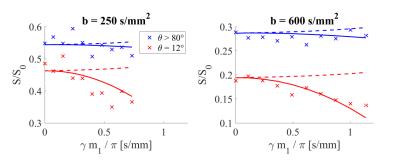
Figure 2 shows the data for ϴ>80° (orthogonal) and ϴ=12° (parallel) to the main diffusion direction of one voxel in the medulla. The signal decreased with increasing m₁ when the diffusion gradient was almost parallel to the main diffusion direction (red crosses). However, this effect was not observed when the gradient was orthogonal to the main diffusion direction in the medulla (blue crosses). Solid lines represent the quadratic fit. Dashed lines represent the expected course when completely incoherent flow is assumed (β_||=β_⊥=0).

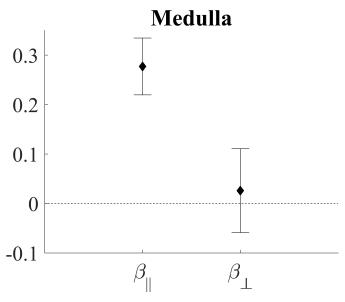
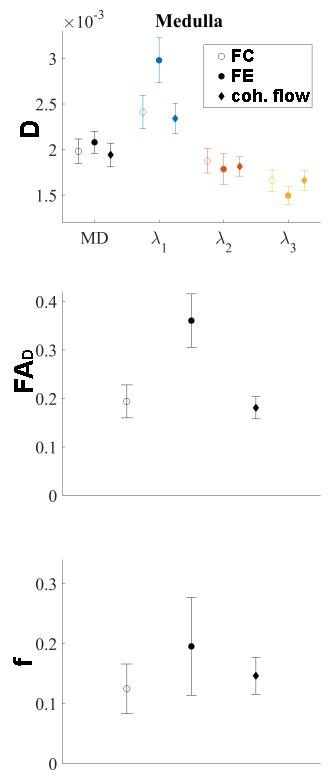
In figure 3 and 4 the data of all voxels in all volunteers is presented as mean ± SD. A fit of all acquired data (0≤m₁≤m_1,max, all gradient directions, all volunteers) to equation (1) resulted in a mean fraction of coherent flow parallel (β_||) to the main direction of diffusion of 0.28 in the medulla (figure 3). However, the fraction of coherent flow orthogonal (β_⊥) to the main diffusion direction did not differ significantly from zero. The resultant parameters of the diffusion tensor D (mean diffusion (MD) and three eigenvalues λ), the fractional anisotropy (FA_D) and the incoherent perfusion fraction (f) of these fits are shown in figure 4 (coh. flow). These findings are compared to results of a fit to either only the flow compensated data (FC) or only the data from maximal flow encoding (FE) to an extended IVIM model (diffusion tensor D and a perfusion fraction f). Results from flow compensated measurements and the evaluation using the coherent flow model matched well, while the results from flow encoded measurements overestimate λ₁, the fractional anisotropy and the perfusion fraction.

Discussion

Conclusion

Acknowledgements

References

[1] Le Bihan et al., Radiology, 168(2):497–505, 1988.
[2] Wetscherek et al., Magnetic Resonance in Medicine, 74(2):410–419, 2015.