0845
Clinically feasible relaxation-diffusion correlation MRI using MADCO1Quantitative Imaging and Tissue Sciences, National Institutes of Health, Bethesda, MD, United States
Synopsis
Even though the brain is microscopically heterogeneous, the majority of currently used quantitative MRI methods in brain research employ idealized models to describe specific structures. Multidimensional relaxation-diffusion correlation (REDCO) is an assumption-free method that measures how water is distributed within the tissue. REDCO had never been used in clinical applications because of the large amount of data it requires. Here we apply the concept of marginal distributions constrained optimization (MADCO) to REDCO-MRI experiments. Using this approach data requirements are vastly reduced, making REDCO-MRI a clinically feasible imaging technique to infer the underlying microstructure, number of compartments, and possibly their function.
Purpose
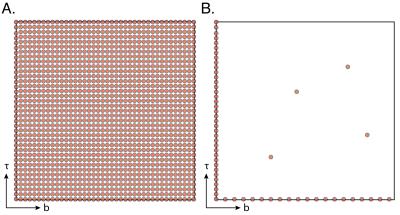
The majority of currently used quantitative MRI methods in brain research employ idealized models to describe specific structures and regions (e.g., axons in white matter are modeled as impermeable cylinders). However, the brain is microscopically heterogeneous. A typical brain volume contains different components, such as axons, glia, myelin, dendrites, and soma, and a mixture of extracellular matrix molecules, neurofilaments, etc. The high level of complexity and variability of brain tissue requires rethinking the use of parametric model-based methods. A promising alternative is to use an assumption-free method to study material samples, such as those used in NMR petrophysics applications: multi-dimensional relaxation-diffusion correlation (REDCO).1 This approach can be used to measure how water is distributed within the tissue, and from it, one can infer the underlying microstructure, number of compartments, their volume fraction and possibly their function. The number of exchange processes can all be quantified, without imposing any a priori assumptions. REDCO can be based on any number of MR contrasts, but typically the relaxation times $$$T_1$$$ and $$$T_2$$$, and the diffusivity are used with a 2D acquisition (Fig. 1A) and analysis framework.2 Combined with MRI, these distributions could provide maps of different neuronal components, possibly allowing for the observation of neuroplasticity at the sub-cellular level. The reason REDCO had never been used in clinical applications, however, is the large amount of data it requires, leading to impractical MRI scan times. Recently, a strategy was introduced that used the marginal 1D distributions of the desired 2D function as equality constraints to stabilize and reduce the number of required acquisitions.3 Here we apply the concept of marginal distributions constrained optimization (MADCO) to multi-dimensional MRI experiments.Methods
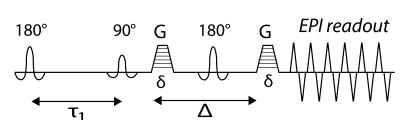
Although the method is equally applicable to other types of multi-dimensional experiments, we chose to demonstrate it on a $$$D$$$-$$$T_{1}$$$ polyvinylpyrrolidone (PVP) water solution phantom. Doped water and PVP were used to create a three-peak MRI phantom. Two purified water samples with 0.18mM and 0.5mM gadopentetate dimeglumine were prepared, along with a 20% w/v PVP water solution sample. The corresponding relaxation times and diffusivities are measured separately for each sample (referred to as Ground Truth, Fig. 3A). MRI data were acquired on a 7T Bruker wide-bore vertical magnet with an inversion recovery DW EPI sequence (details in Fig. 2). For $$$D$$$-$$$T_{1}$$$ measurements, for a given recovery time the fully recovered data are subtracted from the data, and the signal attenuation can be expressed as:
$$M(\tau,b)=\sum_{n=1}^{N_{T_{1}}}\sum_{m=1}^{N_{D}}{{\mathbf{F}(T_{1,n},D_{m})\,\exp(-\frac{\tau}{T_{1,n}})\exp(-bD_{m})}}.$$
In this work we suggest a simple way to stabilize the estimation of $$$\mathbf{F}(T_1,D)$$$ in Eq. 1, while significantly reducing the number of required acquisitions and improving accuracy, by constraining the solution according to the following relations:
$$\sum_{n=1}^{N_{D}}{\mathbf{F}(T_1,D_{n})}=F(T_1) \quad and \quad \sum_{n=1}^{N_{T_1}}{\mathbf{F}(T_{1,n},D)}=F(D). $$
These marginal distributions can be separately estimated from 1D experiments, which require an order of magnitude less data than a conventional 2D acquisition (Fig. 1B).
Results and Discussion
The performance of MADCO was determined and compared with the conventional method. 2D distributions and their 1D projections obtained from MADCO and conventional analyses of the signal using 64 and 1480 acquisitions, respectively, are shown in Figs. 3B-C. Purposely oversampled, the full acquisition scan time was $$$\sim37$$$h. As shown, the $$$D$$$-$$$T_{1}$$$ distribution estimated with the conventional method was far from accurate, even when the full data set was used (Fig. 3C). Conversely, applying the proposed method led to very good agreement with the ground truth distribution (Fig. 3B), even when using only 4% of the full data set (64 acquisitions). With the current experimental parameters 64 acquisitions corresponded to $$$\sim$$$90min in scan time. Although this is a phantom study, we intentionally used an IR-DWI-EPI pulse sequence, which can be used in in vivo preclinical and clinical studies. The repetition time in this study could have been reduced from 10s to the widely used range in in vivo applications of 3s,4 resulting in a total acquisition time of $$$\sim$$$30min. Further acceleration can be achieved by using a version of the Look-Locker acquisition.5Conclusion
The potential impact of this work is directed towards preclinical and clinical applications, where it would allow a comprehensive investigation of compartments and their exchange in a practicable time frame by using the MADCO method in conjunction with a variety of 2D MRI experiments. Currently invisible compartments and inaccessible biological processes that may be implicated in neuroplasticity and learning, in normal and abnormal development, and following disease or neurodegenerative conditions and injury. Furthermore, our work may be extended beyond 2D to higher dimensions since the main limitation of experimental time is now relaxed.
Acknowledgements
No acknowledgement found.References
1. English AE, Whittall KP, Joy MLG, Henkelman RM, Quantitative two-dimensional time correlation relaxometry. Magn Reson Med. 1991;22:425-434.
2. Song Y-Q, Venkataramanan L, Hu¨rlimann M, Flaum M, Frulla P, Straley C, T1-T2 correlation spectra obtained using a fast two-dimensional Laplace inversion. J Magn Reson. 2002;154:261-268.
3. Benjamini D, Basser PJ, Joint radius-length distribution as a measure of anisotropic pore eccentricity: an experimental and analytical framework. J Chem Phys. 2014;141:214202.
4. Mulkern RV, Zengingonul HP, Robertson RL, Bogner P, Zou KH, Gudbjartsson H, Guttmann CR, Holtzman D, Kyriakos W, Jolesz FA, Maier SE, Multi-component apparent diffusion coefficients in human brain: relationship to spin-lattice relaxation. Magn Reson Med. 2000;44:292-300.
5. Look DC, Locker DR, Time saving in measurement of NMR and EPR relaxation times. Rev Sci Instrum. 1970;41:250.
Figures