Synopsis

Time dependence of the brain white matter diffusion-weighted signal originates from both intra-axonal and extra-axonal spaces. Here, we investigate which of these contributions dominates in spinal cord white matter for clinically feasible acquisitions, to inform accurate model-based microstructural imaging. We analyse data from Monte Carlo simulations and from in vivo scans, and find that for diffusion times of 20-70 ms time dependence has mostly intra-axonal origin. Such a time dependence influences the estimation of axonal volume fraction and extra-axonal diffusivity, and highlights the importance of using long diffusion times to support stick-like models for axons in the spinal cord.

Purpose

Recent findings suggest that the time dependence of the diffusion-weighted (DW) magnetic resonance (MR) signal in brain white matter originates not only from the intra-axonal, but also from the extra-axonal space¹, with important modelling implications². However, it is not clear yet which of these contributions dominates for clinically-achievable diffusion times in spinal cord white matter, characterised by larger axons³ than those previously considered¹.

Here, we aim to answer this question, as such information is key for mapping microstructure accurately in spinal cord applications.

Methods

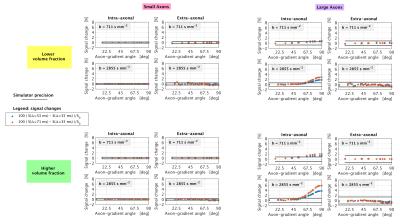
Simulations We ran Monte Carlo simulations in Camino⁴ using 10⁵ spins to obtain signals from two substrates of gamma-distributed, impermeable cylinders, accommodating for myelin (g-ratio: 0.75). We modelled spinal cord white matter (large radii³; mean radius: 3.50 μm, figure 1) and, for comparison, callosal axons (smaller radii⁵; mean radius: 1.29 μm, figure 1), considering two different volume fractions (0.4 and 0.7) and setting 2 μm²/ms for the diffusivity inside/outside the cylinders. Assuming maximum gradient strength of 65 mT/m and TE ≤ 110 ms, we simulated three clinically-feasible pulsed-gradient spin echo (PGSE) protocols (9 b = 0; 20 directions at b = 711 s/mm², 40 at b = 2855 s/mm²), each characterised by δ = 19 ms and a unique Δ amongst {35, 53, 71} ms.

Image acquisition We scanned three healthy volunteers (2 males, 27 years) on a 3T Philips Achieva system at cervical level. Our protocol included: a fast-field-echo (FFE) scan (resolution 0.75×0.75×5 mm³, field-of-view 240×180×60 mm³, TE/TR = 4.1/20 ms/ms, flip angle 7°); three clinically feasible, two-shell DW scans (cardiac-gated PGSE ZOOM; resolution 1×1×5 mm³, field-of-view 64×48×60 mm³, TE = 111 ms; TR 12RR repeats; b-values/directions as simulations; δ = 22 ms), each characterised by a unique Δ amongst {29, 52, 76} ms.

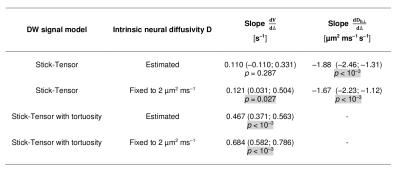
Image analysis Preprocessing was performed with MRtrix3 and SCT (denoising⁶ accounting for noise floor⁷; motion correction⁸; semi-automated white matter segmentation⁹ on FFE scans; co-registration FFE-DW scans⁹). Afterwards, we fitted voxel-by-voxel the following two-compartment signal model to each two-shell scan using Matlab: i) intra-axonal restricted compartment (zero-radius cylinders or “sticks”; volume fraction V); ii) extra-axonal hindered compartment (cylindrically symmetric tensor; perpendicular diffusivity D_h⊥ ≤ D). The model was fitted either fixing D = 2 µm²/ms or estimating D and, for each case, estimating D_h⊥ or fixing it to (1 – V) D (tortuosity limit²).

Statistical analysis We tested for Δ-dependence of V and D_h⊥ fitting in Stata 14.1 a mixed effects model accounting for within-voxel/within-subject correlations (3-level hierarchy; random intercept; random slope).

Results

Simulations Figure 2 illustrates synthetic signal changes when Δ increases at fixed b, for different gradient orientations (signal sensitivity¹⁰). No appreciable changes above the simulation precision can be measured for small axons and for the extra-axonal signal of larger axons. However, the intra-axonal signal of the substrate with larger axons exhibits marked diffusion time dependence.

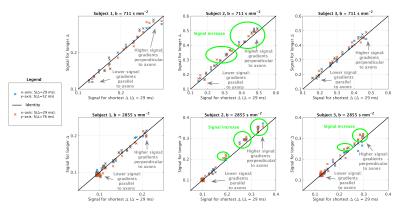
In vivo signals Figure 3 shows scatter plots of signals obtained at minimum Δ versus those obtained at higher Δ. At fixed b, we observe higher signal at high Δ compared to low Δ in subjects 2 and 3 for gradients perpendicular to axons.

Statistical analysis Figure 4 reports the results of the statistical analysis. V increases significantly for increasing Δ when D is fixed, but only for the fitting with D_h⊥ fixed to the tortuosity limit when D is estimated. D_h⊥ always decreases significantly for increasing Δ.

Discussion

We have investigated the time dependence of the DW MR signal in the human spinal cord.

In vivo, at fixed b the DW signal increases as Δ increases, leading to significant decreases of D_h⊥ and increases of V (more evident when D is fixed, owing to ill-posed model inversion). This time dependence is likely to originate mostly in the intra-axonal space, as shown by our simulations, which also point towards negligible signal changes for smaller, callosal-like axons (a finding compatible with other studies^1,2, where wider diffusion time ranges were considered).

The changes in V in vivo are stronger when the tortuosity approximation is employed, while they are weaker without, although still present and detectable. Results suggest that the lowest Δ used here is not sufficient for the perpendicular intra-axonal signal to reach its fully-restricted limit, and also implies that the changes of D_h⊥ may capture changes of the apparent intra-axonal perpendicular diffusivity.

Conclusion

Acknowledgements

References

[1] Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage 2015; 114: 18-37.

[2] De Santis S, Jones DK, Roebroeck A. Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage 2016; 130: 91-103.

[3] Makino M, Mimatsu K, Saito H, et al. Morphometric study of myelinated fibers in human cervical spinal cord white matter. Spine 1996; 21: 1010-1016.

[4] Hall MG and Alexander DC. Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE T Med Imaging 2009; 28(9): 1354-1364.

[5] Alexander DC, Hubbard PL, Hall MG, et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage 2010; 52(4):1374-1389.

[6] Veraart J, Novikov DS, Christiaens D, et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016; 142: 394-406.

[7] Koay CG and Basser PJ. Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. J Magn Reson 2006; 179(2): 317-322.

[8] Grussu F, Schneider T, Zhang H, et al. Neurite orientation dispersion and density imaging of the healthy cervical spinal cord in vivo. NeuroImage 2015; 111: 590-601.

[9] De Leneer B, Lévy S, Dupont SM, et al. SCT: spinal cord toolbox, an open source software for processing spinal cord MRI data. NeuroImage 2016 (in press).

[10] Drobnjak I, Zhang H, Ianus A, et al. PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magn Reson Med 2016; 75(2): 688-700.