0841
Time Dependence Of White Matter Biomarkers From Axially Symmetric Diffusion Kurtosis ImagingJonas Lynge Olsen1, Brian Hansen2, Noam Shemesh3, and Sune Nørhøj Jespersen1,2
1Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark, 2CFIN/MINDLab at the Department of Clinical Medicine, Aarhus University, Aarhus, Denmark, 3Champalimaud Neuroscience Programme, Champalimaud Centre for the Unknown, Lisbon, Portugal
Synopsis
Using a recently developed PFG-based framework for fast diffusion kurtosis imaging we observe a strong time dependence of diffusion and kurtosis metrics in fixed spinal cord white matter from 6-350 ms. DKI metrics can be expressed in terms of intra- and extra axonal properties using white matter tract integrity (biexponential modelling), but a sign ambiguity results in two solutions of the inverse problem. The time dependence of the two solutions observed here help identify the correct solution, and allows comparing time-dependent compartment diffusivities with theory.
Introduction
Non-vanishing diffusion kurtosis and time-dependent diffusion are both hallmarks of nongaussian diffusion in biological tissues. Here we use the 199 fast kurtosis acquisition protocol [1-3] to estimate radial, axial and mean kurtosis and diffusivity with reduced data requirements, allowing us to cover an extended range of diffusion times (6-350 ms ) using the same PFG based sequence. Combined with biophysical modelling, we use this data from spinal cord white matter to provide microstructurally specific information, i.e. axonal water fraction, intra-axonal diffusivity and extracellular diffusivity in radial and axial directions as functions of diffusion time, and compare with effective medium theory. The time dependence of axonal diffusivities help resolve an inherent ambiguity in diffusion modelling related to the relative magnitude of intra- and extra-cellular diffusivity.Methods
Fixed porcine spinal cord was imaged with a stimulated echo diffusion imaging sequence (EPI) on an ultrahigh-field 16.4T Bruker Aeon Ascend magnet (700MHz) equipped with a micro5 probe capable of producing up to 3000mT/m in all directions. Six b=0 images were acquired, as well as six b-values from 500 to 3000 µm2/ms, with nine directions for the 199 DKI scheme each[1]. Other imaging parameters were: 4 averages, TE=16 ms, TR=7.5s, in-plane resolution 140 µm x140 µm. Gradient pulse width was kept constant at 1.15ms, and diffusion times ranged from 6 ms to 350 ms in 57 steps. The raw images were corrected for Gibbs ringing[4] and denoised[5] before the subsequent analysis. Axial, radial, and mean diffusion and kurtosis were estimated with axially symmetric DKI fitting[3], and analysed in seven white matter ROIs: A=dCST – dorsal corticospinal tract, B=FG – Fasiculus Gracilis, C=FC – Fasiculus Cuneatis, D=ReST – Reticulospinal tract, E=RST – Rubrospinal tract, F=STT – Spinothalamic tract, G=VST – Vestibulospinal tract. In these regions of highly aligned axons, biexponential modelling (WMTI[6]) is appropriate at least for sufficiently large diffusion times, and allows kurtosis and diffusion tensors to be expressed in terms of compartmental biophysical parameters: $$$D_{a}$$$ (intra-axonal diffusivity), $$$D_{e,||}$$$ (axial extra axonal diffusivity), $$$D_{e,\bot}$$$ (radial extra axonal diffusivity), and $$$f$$$ (axonal water fraction). These relationships can be analytically inverted in axially symmetric regions, resulting in $$f = (1 + 3/K_{\bot})^{-1}$$ $$D_{e,\bot} = D_{\bot}(1 + K_{\bot}/3)$$ $$D_{e,||} = D_{||}(1 - \eta\sqrt{K_{||}K_{\bot}}/3)$$ $$D_{a} = D_{||} (1 + \eta \sqrt{K_{||}/K_{\bot}})$$ where $$$\eta = \pm 1$$$. The unknown sign $$$\eta$$$ prevents an unambiguous solution for the diffusion coefficients[7, 8]. The long time behavior of the diffusivities has been predicted using effective medium theory[9, 10] $$ D_{a}(t) \sim (D_{a}(\infty) + \frac{c_1}{\sqrt{t}})$$ $$ D_{e,||}(t) \sim (D_{e,||}(\infty) + \frac{c_2}{\sqrt{t}})$$ $$ D_{\bot}(t)\approx (1-f) D_{e,\bot}(t) \sim (1-f)(D_{e,\bot}(\infty) + \frac{c_3}{t}\ln(t/t_c))$$Results
Figure 1 shows the ROI-averaged diffusion (top) and kurtosis metrics (bottom). A pronounced, smoothly decaying time dependence was observed in axial and radial diffusivity, and remarkably, neither seem to have plateaued at 350 ms. Axial kurtosis displays two types of behaviours. In regions D,G a clear nonmonotonic behavior is seen, with a maximum around ~80 ms. Such nonmonotonic behavior is expected, as diffusion is approximately Gaussian at very short and very long diffusion times. (For confined diffusion, $$$K(t)\sim \sqrt{t}$$$ for $$$t\to 0$$$, $$$K(t)\propto 1-\textrm{constant}\cdot\exp(-\lambda_1 t)$$$ for $$$t\to \infty$$$. The remaining ROIs show only decreasing behavior, perhaps because of a smaller characteristic length scale. Radial kurtosis is noisier, but appears to increase over the observable time range. Finally, mean kurtosis increases sharply initially, plateauing above $$$t\sim 100$$$ ms. Figure 2 shows the two branches of intra-axonal diffusivity as function of time. The + branch shows the expected smooth decay of diffusivity for increasing diffusion times, whereas the - branch shows an increasing behavior as a function of diffusion time, although noisier. This indicates that the negative branch is unphysical, and it is therefore discarded in the following. Figure 3 shows the remaining WMTI parameters, f (a), $$$D_{e,||} $$$ (b) and $$$D_{e,\bot}$$$. Although noisy, the axonal water fraction is relatively stable for most ROIs at diffusion times above 100 ms. For lower diffusion times, there is a systematic decrease, which may be due to non-negligible intra-compartmental kurtosis. Extracellular axial diffusivity smoothly decays with time over the entire range, fulfilling $$$D_{e,||}< D_a$$$. Radial diffusivity also decays with time, but with a much lower rate at large diffusion times. Finally, figure 4 demonstrates fits to EMT diffusivity predictions with reasonable agreement. Fit parameters are available from the table.Conclusions
We demonstrated strong time dependence of directional kurtosis and diffusion metrics over an extended range in fixed pig spinal cord. Biophysical modelling revealed intra-axonal diffusivity to typically exceed extracellular axial diffusivity, and effective medium theory provided reasonable predictions.Acknowledgements
Danish Ministry of Science, Technology and Innovation’s University Investment Grant (MINDLab, Grant no. 0601-01354B), and Lundbeck Foundation R83-A7548 .References
1. Hansen, B., et al., Magnetic Resonance in Medicine, 2013. 69(6). 2. Hansen, B., et al., Magnetic Resonance in Medicine, 2015. 3. Hansen, B., et al., NeuroImage, 2016. 4. Kellner, E., et al., Magn Reson Med, 2016. 76(5). 5. Veraart, J., et al., Magn Reson Med, 2016. 76(5). 6. Fieremans, E., et al., Neuroimage, 2011. 58(1). 7. Jelescu, I.O., et al., NMR in biomedicine, 2016. 29(1). 8. Novikov, D.S., et al. (2016) ArXiv e-prints 1609.09144v1 9. Novikov, D.S., et al., Proceedings of the National Academy of Sciences, 2014. 10. Fieremans, E., et al., Neuroimage, 2016. 129.Figures
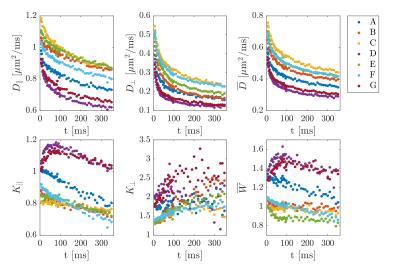
Time dependent axial,
radial, and mean diffusivity (top row) and kurtosis (bottom row)
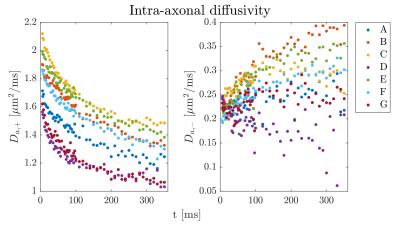
The two solutions
(branches) for intra axonal diffusivity.
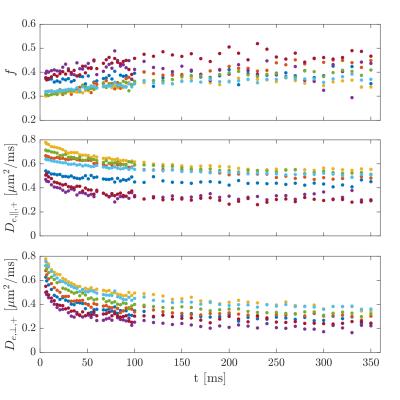
Remaining WMTI
parameters for the most plausible solution.
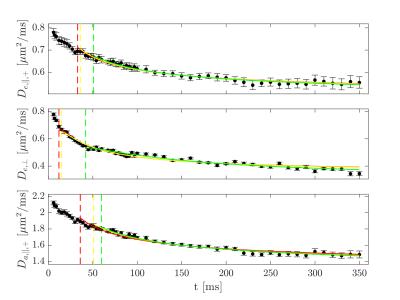
Fits to long time
extra- and intra-axonal diffusivities predicted by effective medium theory. The different colours indicate fits using
different low time cutoffs selected according to the relative change in R2 per
degree of freedom of 1% (green), 3% (yellow), and 5% (red).
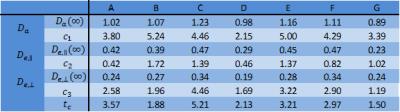
Fitting parameters from effective
medium theory. Diffusivities are in µm2/ms, tc in ms, c1
and c2 are in µm2ms1/2, and c3 is
in µm2.