0839

T1-induced apparent time dependence of diffusion coefficient measured with stimulated echo due to exchange with myelin water

Hong-Hsi Lee¹, Dmitry S. Novikov¹, and Els Fieremans¹

¹Center for Biomedical Imaging, New York University, New York, NY, United States

Synopsis

For diffusion measurements, stimulated-echo acquisition mode (STEAM) has been widely used. To enhance sensitivity to microstructure, previous studies used STEAM to vary the diffusion time by changing the mixing time t_M. Here we show that varying t_M results in an “apparent” STEAM-measured diffusivity dependence on t_M, irrespective of genuine microstructure-specific time dependence. This effect is caused by T₁-relaxation and water exchange between myelin water and "free" water (intra- and extra-axonal water). We propose a modified Kärger model considering diffusion+T₁-relaxation+exchange, and demonstrate that exchange-induced t_M-dependence explains ~20-50% of the total diffusion time dependence, and should be considered while using STEAM.

Purpose

Stimulated-echo acquisition mode (STEAM) has been widely used for diffusion measurements [1]. To enhance the sensitivity to microstructure, previous studies attempted to vary diffusion time $$$\Delta$$$ in a wide range [2,3], achieved by changing mixing time $$$t_M$$$ in STEAM sequence. Here we show that varying $$$t_M$$$ results in an “apparent” STEAM-measured diffusivity dependence on $$$t_M$$$, irrespective of the genuine microstructure-specific time dependence $$$D(t)$$$. This extra $$$t_M$$$ dependence is caused by $$$T_1$$$-relaxation and water exchange between myelin water and "free" water (intra- and extra-axonal water) [3]. We develop a theoretical framework for this effect based on solving a modified K$$${\rm\ddot{a}}$$$rger model incorporating longitudinal relaxation [4-6]. Furthermore, we demonstrate exchange-induced $$$t_M$$$-dependence in human brain white matter (WM), and subsequently correct for it, revealing the genuine $$$D(t)$$$ dependence. Exchange-induced $$$t_M$$$-dependence explains ~20-50% of the total diffusion time dependence, and should be considered when interpreting diffusion experiments using STEAM.

Theory

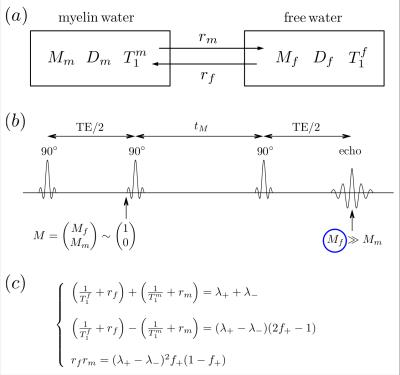
For human brain WM, we proposed a diffusion+relaxation+exchange model shown in Fig.1a, where $$$M_f$$$ and $$$M_m$$$ are magnetizations of ”free” and myelin water. It is the K$$${\rm\ddot{a}}$$$rger model [4,5] for a two-component magnetization $$$M\sim\begin{pmatrix}M_f\\M_m\end{pmatrix}$$$, but with a modified initial condition for the evolution during the $$$t_M$$$ interval: the observed signal comes only from the “free” pool, i.e. the initial condition $$$\sim\begin{pmatrix}1\\0\end{pmatrix}$$$, and the measurement (at t>$$$t_M$$$) projects the evolution back onto the “free” pool, because of short myelin water T$$$_2\ll$$$TE (Fig.1b) [7]. The result is that the apparent diffusion coefficient (ADC) in the free water acquires $$$t_M$$$-dependence even if both compartment diffusivities are constant---in stark contrast to the regular K$$${\rm\ddot{a}}$$$rger model, where exchange does not lead to extra time-dependence [4,5].

In this model (Fig.1a), myelin water has diffusivity $$$D_m$$$, longitudinal relaxation time $$$T_1^m$$$, and free water has $$$D_f$$$ and $$$T_1^f$$$, respectively. The exchange rates are $$$r_m$$$ (from myelin to free) and $$$r_f$$$ (from free to myelin), conforming to the detailed balance [4,5].

For this modified K$$${\rm\ddot{a}}$$$rger model, the Bloch-Torrey equation is given by [6]$$\partial_t M=(D\nabla^2-i\gamma\,g\cdot\,r-R_L-R_E)\cdot\,M,\quad\quad(1)$$ where $$$M=\begin{pmatrix}M_f\\M_m\end{pmatrix},\,D=\begin{pmatrix}D_f&0\\0&D_m\end{pmatrix},\,R_L=\begin{pmatrix}1/T_1^f&0\\0&1/T_1^m\end{pmatrix}$$$, and $$$R_E=\begin{pmatrix}r_f&-r_m\\-r_f&r_m\end{pmatrix}$$$.

Solving Eq.(1) with the initial condition $$$\sim\begin{pmatrix}1\\0\end{pmatrix}$$$ based on previous discussion, the non-diffusion weighted signal [6]$$S_{b=0}=f_+\cdot\,e^{-\lambda_+\cdot\,t_M}+f_-\cdot\,e^{-\lambda_-\cdot\,t_M},\quad\quad(2)$$ where $$$f_++f_-=1$$$. $$$S_{b=0}$$$ is normalized to 1 for $$$t_M$$$=0. Fitting parameters ($$$f_+,\,\lambda_+,\,\lambda_-$$$) are combinations of tissue parameters ($$$T_1^f,\,T_1^m,\,r_f,\,r_m$$$), shown in Fig.1c. The myelin water residence time $$$\tau_m=1/r_m$$$ is roughly estimated by $$$\sim\,1/\sqrt{r_fr_m}$$$. Without water exchange ($$$r_f=r_m=0$$$), Eq.(2) degenerates to a mono-exponential decay $$$S_0=e^{-\lambda\cdot\,t_M}$$$.

Solving for the signal at finite $$$q$$$ and expanding up to $$$q^2$$$, we get our main result: the ADC measured via STEAM DTI is given by $$D_{\rm\,app}=D_f-(D_f-D_m)\cdot\,f_+\cdot\frac{1-\frac{\tau}{t_M}+\left(1+\frac{\tau}{t_M}\right)e^{-2t_M/\tau}}{1+\frac{f_+}{f_-}e^{-2t_M/\tau}}\cdot\frac{t_M}{\Delta-\delta/3},\quad\quad(3)$$ where $$$\tau=2/(\lambda_+-\lambda_-)$$$, and $$$\delta$$$ is diffusion gradient pulse width. To stabilize our fitting, we fixed myelin diffusivities: axial $$$D_m^\parallel\sim$$$0.5μm$$$^2$$$/ms and radial $$$D_m^\perp\sim$$$0.2μm$$$^2$$$/ms [8]. The case of $$$D_m^\parallel$$$=$$$D_m^\perp$$$=0 is also shown to discuss the influence of $$$D_m$$$ on corrections.

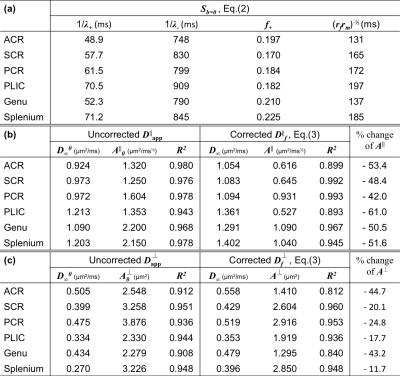
We also applied models for time-dependent diffusion [3,9,10] to the measured $$$D_{\rm\,app}$$$ and the calculated $$$D_f$$$ after correction for exchange (Table 1).

Materials and Methods

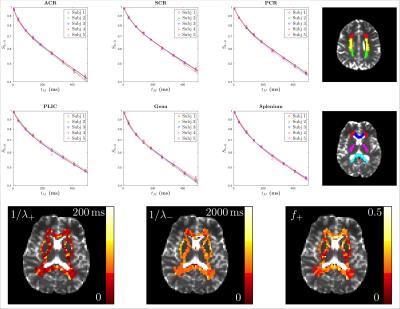
Diffusion measurements were performed on five healthy subjects (4males/1female, 23-27y/o) using a 3T Siemens Prisma scanner with a 64-channel head coil. We used a STEAM sequence provided by the vendor (Siemens WIP 511E). TE/TR=100/11900ms, resolution=(2.7mm)$$$^3$$$, FOV=(221mm)$$$^2$$$. For each $$$\Delta$$$, we acquired three $$$b=0$$$ images and $$$b=500$$$s/mm$$$^2$$$ images along 20 diffusion gradient directions. We varied $$$\Delta=71-550$$$ms and $$$t_M$$$=5.5-484.5ms, and fixed $$$\delta=8$$$ms. A series of WM regions-of-interest (ROIs) were created based on the JHU DTI WM atlases (anatomical WM ROI) (Fig.2) [11]. The axial and radial diffusivities were averaged over each ROI and corrected for each subject by using Eq.(3).

Results

Fig.2 shows for each ROI bi-exponential decay of the $$$b=0$$$ signal $$$S_{b=0}$$$, instead of mono-exponential, with respect to $$$t_M$$$ (Eq.(2)) with two time scales $$$1/\lambda_+$$$~65ms and $$$1/\lambda_-$$$~830ms, and the estimated myelin residence time is $$$\tau_m\sim160$$$ms (Table 1a), consistent with previous studies [12], manifesting effects of water exchange and $$$T_1$$$-relaxation.

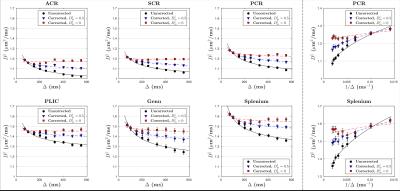
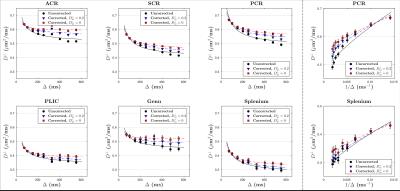
The uncorrected ADC ($$$D_{\rm app}^\parallel,\,D_{\rm app}^\perp$$$) and calculated free water diffusivities ($$$D_f^\parallel,\,D_f^\perp$$$), based on Eq.(3), with respect to $$$\Delta$$$, are both shown in Figs.3 and 4. The fitting parameters of time dependence models are shown in Table 1b-c. In general, ~20-50% of the diffusion time dependence, indicated by strength of restrictions ($$$A^\parallel,\,A^\perp$$$), is contributed to exchange.

Discussion and Conclusion

Varying $$$t_M$$$ in STEAM introduces a $$$t_M$$$-dependent diffusion in human brain WM, caused by water exchange between myelin water and "free" water with different $$$T _1$$$ values. In WM, ~20-50% of the "diffusion time" dependence results from this effect.

Remarkably, STEAM provides an “orthogonal” contrast to monopolar pulsed-gradient spin-echo (PGSE); hence, using both sequences, or providing the correction described above based on the $$$S_{b=0}$$$ signal, may enable simultaneous mapping of microstructural and relaxational tissue parameters.

Acknowledgements

We would like to thank Thorsten Feiweier for developing the advanced diffusion WIP sequence and Jelle Veraart for assistance with image processing. Research was supported by the National Institute of Neurological Disorders and Stroke of the National Institutes of Health under award number R01NS088040.

References

[1] Merboldt, K.D., et al. JMR 64(3),479-486 (1985).

[2] Assaf, Y., et al. MRM 59:1347-1354 (2008).

[3] Fieremans, E., et al. NI 129,414-427 (2016).

[4] K$$${\rm\ddot{a}}$$$rger, J. Adv. Colloid Interface Sci. 23,129-148 (1985).

[5] Fieremans, E., et al. NMR Biomed. 23,711-724 (2010).

[6] Stanisz, G.J., et al. MRM 39,223-233 (1998).

[7] Whittal, K.P., et al. MRM 37,34-43 (1997).

[8] Andrews, T.J., et al. MRM 56,381-385 (2006).

[9] Novikov, D.S., et al. PNAS 111,5088-5093 (2014).

[10] Burcaw, L.M., et al. NI 114,18-37 (2015).

[11] Mori, S., et al. MRI atlas of human white matter. Elsevier (2005).

[12] Rioux, J.A., et al. MRM 75(6),2265-2277 (2016).

Figures

Fig.1. (a) A modified K$$${\rm\ddot{a}}$$$rger model (two-component model) for the brain WM, composed of myelin water and “free” water, and its corresponding tissue parameters [4,5]. (b) In a STEAM sequence, myelin water magnetization $$$M_m$$$ decays away at t=TE/2 and t=$$$t_M$$$+TE since myelin water T$$$_2\ll$$$ TE [7]. Therefore, signal is generally contributed by free water. (c) The three fitting parameters ($$$\lambda_+,\,\lambda_-,\,f_+$$$) in Eq.(2) are combinations of the four tissue parameters ($$$T_1^f,\,T_1^m,\,r_f,\,r_m$$$) in Fig.1a.

Fig.2. Signal $$$S_{b=0}$$$ in $$$b$$$=0 images decays with mixing time $$$t_M$$$ in a bi-exponential fashion, manifested by the curve, instead of a straight line, in a semi-log plot. The bi-exponential decay conforms to Eq.(2), indicating the effect of T$$$_1$$$-relaxation and water exchange. Table 1a shows corresponding fitting parameters. WM ROIs are shown in the right column. One subject’s parametric maps are shown in the lower row. ACR (red)= anterior corona radiata, SCR (yellow)= superior corona radiata, PCR (green)= posterior corona radiata, PLIC (magenta)= posterior limb of the internal capsule, Genu (blue) and Splenium (cyan) of the corpus callosum.

Fig.3. Measured axial diffusivity $$$D^\parallel_{\rm\,app}$$$ (black circle) in each WM ROI is corrected based on Eq.(3) and parameters in Table 1a. Assuming that axial diffusivities of the myelin water $$$D_m^\parallel$$$ is negligible, $$$D^\parallel_f$$$ would be over-corrected (red square), especially at long diffusion time $$$\Delta$$$. Using a typical value of $$$D_m^\parallel$$$~0.5μm$$$^2$$$/ms [8], corrected $$$D^\parallel_f$$$ (blue triangle) does not show the over-correction and gradually approaches bulk diffusivity at long $$$\Delta$$$. Curves in each subfigure are fits based on $$$D^\parallel\simeq\,D_\infty+\frac{2A^\parallel}{\sqrt{\Delta}}$$$ [3,9], where $$$D_\infty$$$ is bulk diffusivity, and $$$A^\parallel$$$ is strength of restrictions. Figures of $$$D^\parallel$$$ vs. $$$1/\Delta$$$ are shown in the right column.

Fig.4. Measured radial diffusivity $$$D^\perp$$$ (black circle) in each WM ROI is corrected based on Eq.(3) and parameters in Table 1a. Assuming that radial diffusivities of the myelin water $$$D_m^\perp$$$ is negligible, the correction for $$$D^\perp$$$ is large (red square). By using $$$D_m^\perp$$$~0.2μm$$$^2$$$/ms [8], corrections are smaller (blue triangle). Curves in each subfigure are fits based on $$$D^\perp\simeq\,D_\infty+A^\perp\cdot\frac{\ln(\Delta/\delta)}{\Delta}$$$ [3,9], where $$$D_\infty$$$ is bulk diffusivity, and $$$A^\perp$$$ is strength of restrictions. Figures of $$$D^\perp$$$ vs. $$$1/\Delta$$$ are shown in the right column. Corrected $$$D^\perp$$$ increases nonlinearly with 1/$$$\Delta$$$, indicating that time dependence model for $$$D^\perp$$$ is applicable to corrected data.

Table 1. (a) Parameters obtained by fitting Eq.(2) to $$$S_{b=0}$$$. (b) Parameters ($$$D_\infty,\,A^\parallel$$$) obtained by fitting the time dependence of axial diffusivities $$$D^\parallel\simeq\,D_\infty+\frac{2A^\parallel}{\sqrt{\Delta}}$$$ [3,9], with or without corrections based on Eq.(3) and $$$D_m^\parallel$$$ = 0.5 μm$$$^2$$$/ms. (c) Parameters obtained by fitting the time dependence of radial diffusivities $$$D^\perp\simeq\,D_\infty+A^\perp\cdot\frac{\ln(\Delta/\delta)}{\Delta}$$$ [3,9], with or without corrections based on Eq.(3) and $$$D_m^\perp$$$ = 0.2 μm$$$^2$$$/ms. The % change of diffusion time dependence with and without corrections for water exchange is estimated by the % change of strength ($$$A^\parallel$$$, $$$A^\perp$$$) of restrictions.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0839