Synopsis

We resolve degeneracies in the estimation of parameters of white matter integrity by exploiting the observed echo time dependency of diffusion MRI signal in human brain white matter. Empirical results and statistical analyses reveal that adding compartment-specific T₂ relaxation times to biophysical models of diffusion MRI improves the parameter estimation in terms of precision and accuracy.

Purpose

To resolve degeneracies in diffusion MRI parameter estimation of neuronal microstructure, and to determine compartmental $$$T_2$$$ relaxation times.

Biophysical modeling of the diffusion-sensitized MRI (dMRI) signal is the way to achieve specificity, not just sensitivity, to tissue microstructure. Unfortunately, parameter estimation for dMRI models is degenerate.^1,2 In particular, it has been shown empirically and analytically that (at least) two branches of model parameters, often both biophysically plausible, fit dMRI data equally well. Here we report a nontrivial dMRI signal dependence on echo time (TE) in human brain in vivo. We demonstrate, empirically and theoretically, that this TE dependence, which we interpret as originating from compartment-specific $$$T_2$$$ values^3,4, is a promising "orthogonal measure" able to break the degeneracy in parameter estimation, and also yield important relaxational metrics.

Methods

We extended a widely used two-compartment biophysical model^2,5-7 of water inside narrow impermeable "sticks" representing axons, embedded in an extra-cellular matrix, by including the compartment-specific $$$T_2$$$-relaxation parameterized by $$$T_2^a$$$ and $$$T_2^e$$$ for the axonal and extra-axonal compartments, respectively: $$S_\mathbf{\hat{g}}\mathrm{(}b,\,T_E)\,=\,S(0,0)\cdot\int_{|\mathbf{\hat{n}}\mathrm{|}=1}\,d\mathbf{\hat{n}}\mathcal{P}\mathrm{(}\mathbf{\hat{n}}\mathrm{)}\mathcal{K}\mathrm{(}b,T_E,\mathbf{\hat{g}}\cdot\mathbf{\hat{n}}\mathrm{)},\quad(1)$$

with

$$\mathcal{K}(b, T_E, \xi)=fe^{-T_E/T_2^a-bD_a\xi^2}+(1-f)e^{-T_E/T_2^e-bD_e^\perp\,-b(D_e^\parallel-D_e^\perp)\xi^2}\quad(2)$$

being the signal response of a individual fiber fascicle, and $$$S(0,0)$$$ the proton density. We adopt the recently introduced rotationally invariant framework^2,7 that allows limiting the dimensionality of the parameter space by factoring out the axonal orientation distribution function (ODF) $$$\mathcal{P}({\bf\hat{n}})$$$. Basically, we solve an equivalent system

$$S_{l}(b,T_E;x)=p_l\,K_l(b,T_E;x)\quad(3)$$

where rotational invariants of the signal and ODF

$$S_l^2=\sum_{m=-l}^l |S_{lm}|^2/4\pi(2l+1),\quad\mathrm{and}\quad\,p_l^2=\sum_{m=-l}^l |p_{lm}|^2/4\pi(2l+1),\quad(4)$$

one for each $$$l$$$, are constructed from their spherical harmonics coefficients. The projections $$$K_l(b,T_E;x)$$$ of kernel (2) onto Legendre polynomials include explicit $$$T_E$$$ dependence. Here $$$x$$$ denote scalar model parameters including $$$T_2^a,\,T_2^e$$$, axonal volume fraction ($$$f$$$), intra-axonal diffusivity ($$$D_a$$$), parallel and perpendicular extra-axonal diffusivity ($$$D_e^\parallel$$$ and $$$D_e^\perp$$$). The spherical mean technique^8,9 effectively corresponds to a constrained version of the $$$l=0$$$ rotational invariant, $$$K_0$$$. Here we include up to the 2nd order invariant^2,7 $$$K_{0,2}$$$, involving the axonal dispersion $$$p_2$$$, which provides an important extra equation, and do not apply any constraints on scalar parameters $$$x.$$$ Including $$$K_{0,2}$$$, together with experimentally varying $$$T_E$$$, constitutes a novel parameter estimation framework which we refer to as TEdDI, TE dependent Diffusion Imaging.

Data

Results

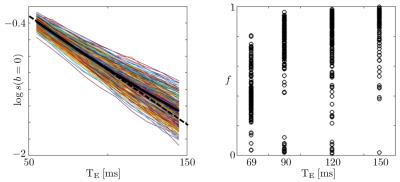
Figure 1: The logarithm of the non-diffusionweighted signal, and the estimated $$$T_2$$$-weighted axonal fraction are shown as function of $$$T_E$$$ for all voxels of the posterior limb of the internal capsule (PLIC). The non-monoexponential signal decay and monotonically changing fraction support the hypothesis of having compartment-specific $$$T_2$$$'s in the white matter (WM). Other ROIs, including corpus callosum (CC), show similar trends (unlike¹⁰).

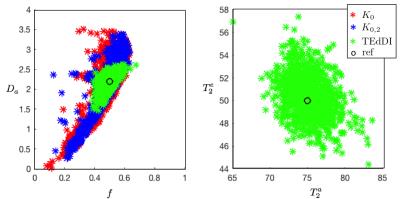
Figure 2: A statistical analysis of TEdDI using the inverse of the Fisher matrix, the covariance matrix of the model variables, predicts that by exploiting the $$$T_E$$$ dependence of the dMRI signal, the coefficient of variation of the model parameters lowers and, at least equally important, the correlation between parameters (e.g. $$$f$$$ and $$$D_a$$$) decreases. The analysis depends on a set of reference values for the model parameters, signal-to-noise ratio (SNR), and acquisition protocol. We adopted these settings from our clinical data.

Figure 3: The decoupling of parameters, e.g. $$$f$$$ and $$$D_a$$$, turns out to be essential to overcome the degeneracy of the biophysical models. Simulations with random noise realizations and optimization initializations confirm these statistical results. Our analysis reveals that compartment $$$T_2$$$’s vary widely across different WM structures of interest.

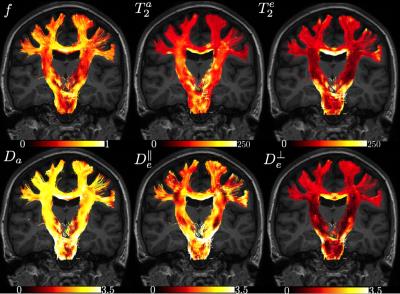
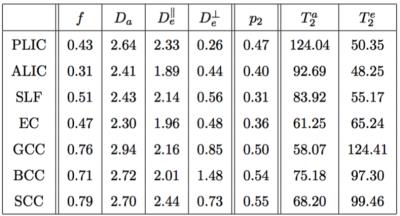
Maps are shown in Figure 4 and average ROI values are tabulated in Figure 5. Partial voluming with cerebrospinal fluid (CSF) that is characterized with high $$$T_2$$$ render the two-compartment model inaccurate around e.g. the CC/CSF border.

Discussion & Conclusion

$$$\bullet$$$ Empirical evidence is given for the $$$T_2$$$ values of intra- and extra-axonal water to be different.

$$$\bullet$$$ While more detailed study is needed, the tract-specific compartmental $$$T_2$$$’s may become valuable parameters in studying WM microstructure.

$$$\bullet$$$ The observed heterogeneity in $$$T_2$$$ values is not yet well understood, but already highlights the potential biases that might arise from assuming prior knowledge or globally fixing parameters, e.g. for kernel-driven diffusion methods such as constrained spherical deconvolution.

$$$\bullet$$$ Exploiting the $$$T_E$$$ dependence by including the compartmental $$$T_2$$$’s in the biophysical models bypasses several intrinsic problems of parameter estimation, resolving the previously highlighted degeneracies^1,2.

Acknowledgements

References

1. Jelescu et al., NMR Biomed 29, 33 (2016)

2. Novikov et al., Proc. ISMRM 2015, p.469; preprint https://arxiv.org/abs/1609.09144

3. Harkins et al. MRM 76(3): 793-800 (2012)

4. De Santis et al. ISMRM abstract 1998 (2016)

5. Jespersen et al., NeuroImage 34, 1473 (2007)

6. Jespersen et al., NeuroImage 49, 205 (2010)

7. Reisert et al., NeuroImage, DOI:10.1016/j.neuroimage.2016.09.058

8. Kaden et al., MRM 75, 1752-1763 (2016)

9. Kaden et al., NeuroImage 139, 346-359 (2016)

10. Ferizi et al. NeuroImage 118: 468-483 (2015)