Introduction

In MRI, in-plane and through-plane resolutions are usually not bound to each other. The acquired image slices tend to be thicker than the resolution of the image plane. In particular,if SNR plays a role, the increase of slice thickness is an easy way to reduce noise. However in several applications, an isotropic image resolution is desired. For example, in diffusion weighted MRI and tractography, isotropic imaging resolution and SNR is quite important.Simple upsampling techniques like linear, cubic or spline interpolation produce block like, jagged-edge artifacts that are disturbing and produce non-natural looking images [1]. In this work we propose a simple and fast method to increase the through-plane image resolution. The idea uses the high resolution edge information in adjacent transversal slices to interpolate in an edge preserving manner.

Method

Suppose a volumetric MR-image $$$I(x,y,z)$$$ with voxel sizes $$$s_p,s_p,s_z$$$ is given, where $$$s_p$$$ is the in-plane voxel size for $$$x$$$ and $$$y$$$ and $$$s_z$$$ is the voxel size in slice direction. The idea is to register image plane with z-index $$$z_i$$$ onto the neighboring image planes $$$z_{i+1}$$$ in a non-rigid way. This estimation problem is also known from so called optical flow estimation [2], where the z-index is the time. For small deformations, the objective can be rewritten in terms of partial derivatives, i.e. we search for a deformation field $$$v = (v_x,v_y)$$$ which minimizes \[ J(v) = \int | v_x \partial_x I + v_y \partial_y I - \partial_z I)|^2 \ dx\ dy \] where $$$\partial_x$$$, $$$\partial_y$$$ and $$$\partial_z$$$ are partial derivatives along $$$x$$$,$$$y$$$ and $$$z$$$, respectively. To solve such a problem we used the original approach by [1], which is a non-iterative method relying only on first-order partial derivatives. Suppose we have determined the optimal deformation field $$$v$$$, then, it is straight-forward to interpolate between slices by \[ (1-\alpha) I(x+ \alpha v_x,y+ \alpha v_y,z_{i}) + \alpha I(x-(1-\alpha) v_x),y- (1-\alpha) v_y,z_{i+1}) \] where $$$\alpha$$$ is a parameter between $$$0$$$ and $$$1$$$ which smoothly interpolates between slices $$$z_i$$$ and $$$z_{i+1}$$$. Depending on the anisotropy of the voxel several types of schemes are possible. One can either insert several new interpolated slices in between the original ones, or in case of $$$s_z/s_p = 2$$$ we used $$$\alpha = 0.25$$$ and $$$\alpha = 0.75$$$ and ignored the original slices. In this way, the noise behavior of all slices is the same.

Results

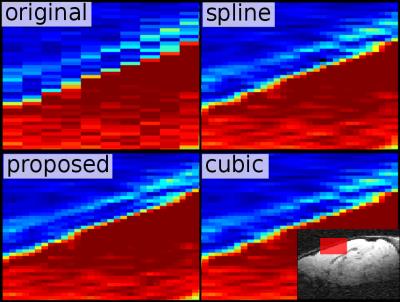
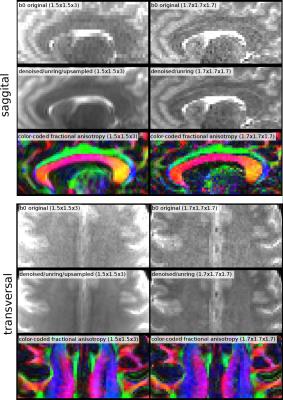
First, we applied the proposed algorithm to a mouse dataset (7T animal scanner, Biospec 70/20, head-adapted cryocoil, Turbo RARE T2, $$$51\times51\times300 \mu m^3$$$, TE/TR = 50 ms/6,514 ms), which was upsampled in slice direction by a factor of $$$3$$$ (Figure 1). Second, we applied the idea on a isotropically sampled MP2rage of the human head (Siemens PRISMA, 32-headcoil, TE/TR = 2.8ms/5000ms, $$$1mm^3$$$ isotropic), but downsampled the image artificially in saggital direction, thus, we have a kind of ground truth (Figure 2). Finally we applied the idea on a diffusion with $$$1.5\times1.5\times3 mm$$$ resolution (Siemens PRISMA, 32-headcoil, TE/TR = 81ms/2800ms, SMS-factor 2, 118 DW-direction at $$$b=1ms/\mu m^2$$$, 12 b0 images ) and, for comparison, a dataset with $$$1.7mm$$$ isotropic (65 DW-direction and $$$b=1ms/\mu m^2$$$, 8 b0 images). For both datasets we applied denoising [3] and Gibbs-ringing removal [4]. Then, we upsampled the first dataset in slice-direction as described above (Figure 3).

Discussion

The mouse example in Figure 1 shows that the typical jagged-edges can be suppressed by the proposed interpolation scheme. Neither spline nor cubic interpolation can avoid that. Although noise produces horizontal stripe-like artifacts, the proposed method produces 'original' looking images. The same holds for the MP2rage example. While cubic upsampling produces block-like artifacts for diagonal structures, the proposed method gives an image which is structurally more consistent with the original image, with some amount of additional smoothness. The diffusion example shows that it is actually possible to gain SNR while seemingly not loosing much resolution. The reference protocol was designed to keep the acquisition time the same if volume coverage is the same. The isotropic protocol needs by a factor of 3/1.7 more slices, which is approximately the ratio of totally acquired images (130/73). For a typical $$$T_2$$$, we can expect that the anisotropic protocol has an SNR gain of approximately $$$\sqrt 2\cdot 3\cdot 1.5^2 e^{-81ms/T_2 } / (1.7^3 e^{-69ms/T_2}) \approx 1.7$$$ compared to the isotropic protocol. The comparison of the two diffusion sequences shows that it is possible to acquire a large amount of diffusion gradient direction within a reasonable time with a good spatial resolution. In fact, for full brain coverage both protocols need about 6min of acquisition time, which fullfills clinical demands.

Acknowledgements

This study was supported by Deutsche Forschungsgemeinschaft (German Research Council) via grants DFG RE 3286/2-1 and DFG KI 1089/3-2.