0756
The Optimality Principle for MR signal excitation and reception: new physical insights into ideal RF coil design1Center for Advanced Imaging Innovation and Research (CAI2R) and Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University School of Medicine, New York, NY, United States, 2Sackler Institute of Graduate Biomedical Sciences, New York University School of Medicine, New York, NY, United States
Synopsis
Despite decades of collective experience, RF coil optimization has remained a largely empirical process, with clear insight into what might constitute truly task-optimal, as opposed to merely “good,” coil performance being difficult to come by. We introduce a new principle, the Optimality Principle, which allows one to predict the form of signal-optimizing current patterns on any arbitrary surface, using a simple conceptual framework. After a brief derivation of the principle, we illustrate its use in generating ideal current patterns for various experimental conditions, and in understanding the emergence of electric dipoles as strong performers at high frequency.
Introduction
Throughout the history of MR, RF coil optimization has remained a largely empirical process, since the complexity of Maxwell’s equations generally prevents all but the most seasoned experts from gaining clear intuition about what might constitute a truly task-optimal, as opposed to a merely “good,” coil performance. Ideal current patterns derived from electrodynamic simulations in simple geometries have been explored in recent years,1 as a guide for design intuition. Since these patterns emerge from a complex numerical optimization procedure, however, the underlying structures that make them truly ideal have remained elusive. The goal of the current work is to describe, and to illustrate implications of, a new principle that provides direct insight into the physical origin of ideal current patterns. We call this principle the “Optimality Principle” (OP), since it allows one to predict the form of signal-optimizing current patterns using a simple conceptual framework. Here, we provide a brief derivation of the principle, then explore some of its implications and predictions.Theory and Methods
The Optimality Principle, in its simplest form, states that the surface current pattern associated with optimal transmit field (B1(+)) or receive sensitivity (B1(-)) (per unit current) at a point of interest is directly proportional to the tangential electric field pattern that would be generated on the surface by a precessing spin placed at that point.
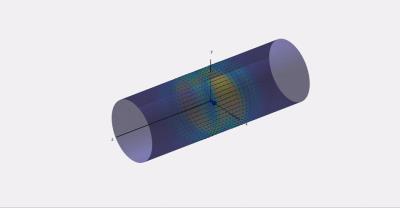
Figure 1 sketches a derivation of the principle for the case of signal reception. (For brevity, a full derivation of the reciprocity principle2,3 transformation used in step 2 has been omitted from the figure, but a simple, step-by-step derivation is available elsewhere4.) Figure 2 shows a sample ideal current pattern on a cylindrical surface surrounding a dielectric cylinder at 7 T.
The result that Jideal ~ Espin, tangential holds as long as noise a) is uncorrelated among the surface current modes, Jn, and b) scales with the current amplitude of each mode. This condition is satisfied when coil noise is dominant. When body noise dominates, the noise covariance matrix ψ mixes modes and distorts the projection. In this case, an iterative approach based on perturbation theory may be used to solve the general expression in Eq. (3) of Figure 1. Unlike analytic dyadic Green’s function formalisms limited to simple geometries,1 the perturbative OP approach enables computation of ideal current patterns, incorporating the effects of body noise, for any arbitrary surface topology and body model, with a limited number of calls to an electrodynamic solver of choice.
Results
Figure 3 compares snapshots of ideal current patterns on a cylinder at very low (0.1T) and very high (7T) magnetic field strength, either including or neglecting the effects of body noise. Without considering body noise, OP patterns for a central point match the tangential electric fields for a central spin: at all field strengths, they are dominated by z-directed currents reminiscent of electric dipoles. At low field, the need to minimize internal electric fields associated with body noise introduces “dark mode” patterns, which contribute no signal at the point of interest, but effectively return the ideal patterns to familiar closed loops. At high field, dark modes have only a minor contribution, and the ideal patterns retain a significant non-closed character. Additional effects resulting from spatial variations in electrical properties can be studied using perturbative OP calculations.
Figures 4 and 5 illustrate a leading hypothesis as to why considerations of body noise minimization penalize non-closed current patterns at low field but not at high field: the continuity equation requires charge separation for non-closed patterns, and this results in notably different contributions to electric field, and therefore body noise, at different field strengths.
Note that quite distinct current patterns are expected for different surface topologies. Indeed, the results for a spherical surface are notably different than for a cylinder:5,6 since a point at the center of a sphere is equidistant from all points on the surface, for example, OP immediately predicts that closed current patterns will be optimal for this configuration at all field strengths.
Discussion and Conclusions
Like the Principle of Reciprocity from which it is derived, the Optimality Principle offers both a conceptual and a computational shortcut, allowing one to arrive immediately at quantitative ideal conductor patterns for arbitrary surface and body geometries with a minimum of computation, simply by switching perspective to a reciprocal transmission process. Here, we have used OP to separate signal and noise effects in coil optimization, to understand the emergence of electric dipoles as strong performers at high frequency,7,8,9 and more generally to highlight the importance of surface topology in coil design.Acknowledgements
The Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net) at New York University School of Medicine is supported by NIH/NIBIB grant P41 EB017183.References
1. Lattanzi R, Sodickson DK. Ideal current patterns yielding optimal signal-to-noise ratio and specific absorption rate in magnetic resonance imaging: computational methods and physical insights. Magn Reson Med 2012;68(1):286-304.
2. Hoult DI, Richards RE. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J Magn Reson 1976;24:71-85.
3. Hoult DI. The Principle of Reciprocity in Signal Strength Calculations - A Mathematical Guide. Concepts Magn Reson 2000;12:173-187.
4. Sodickson DK. Understanding Reciprocity. ISMRM 2017, submitted.
5. Vaidya M, Collins CM, Sodickson DK, Carluccio G, Lattanzi R. Disentangling Signal Propagation and Noise-Related Effects in the Presence of High Permittivity Materials Via Ideal Current Patterns. ISMRM 2016, #391.
6. Vaidya M, Sodickson DK, Collins CM, Lattanzi R. Visualizing the role of the Ideal current patterns in minimizing sample noise using dark mode current patterns for a spherical sample. ISMRM 2017, submitted.
7. Raaijmakers AJ, Ipek O, Klomp DW, Possanzini C, Harvey PR, Lagendijk JJ, van den Berg CA. Design of a radiative surface coil array element at 7 T: the single-side adapted dipole antenna. Magn Reson Med 2011;66(5):1488-1497.
8. Chen G, Lattanzi R, Sodickson DK, Wiggins GC. Approaching the Ultimate Intrinsic SNR with Dense Arrays of Electric Dipole Antennas. ISMRM 2016, #168.
9. Sodickson DK, Wiggins GC, Chen G, Lakshmanan K, Lattanzi R. More Than Meets the Eye: The Mixed Character of Electric Dipole Coils, and Implications for High-Field Performance. ISMRM 2016, #389.
Figures