0749
The ultimate intrinsic SNR in a spherical phantom with regard to an open-pole surface current distribution at 9.4T1High-Field MR Center, Max Planck Institute for Biological Cybernetics, Tuebingen, Germany, 2Institute of Physics, Ernst-Moritz-Arndt University Greifswald, Greifswald, Germany
Synopsis
RF coils for human head imaging need to provide access for the human neck and cannot be entirely closed. In this work, we investigate the ultimate intrinsic signal-to-noise ratio (UISNR) in a spherical phantom due to an open-pole surface current distribution, where the generic surface current patterns run on a spherical cap. The influence of the cap’s opening angle ϑ0 on UISNR, parallel imaging performance and on the contribution of curl-free and divergence-free current patterns to UISNR is studied.
Purpose
The contribution of curl-free and divergence-free current patterns to the ultimate intrinsic signal-to-noise ratio (UISNR) can be evaluated by a spherical surface current distribution, which is completely surrounding a head-like phantom (1) or a voxel model (2). However, RF coils for human head imaging need to provide access for the human neck and cannot be entirely closed. In this work, for the first time, we present the contribution of curl-free and divergence-free current patterns to UISNR regarding an open-pole surface current distribution and investigate the effect of the opening angle.Methods
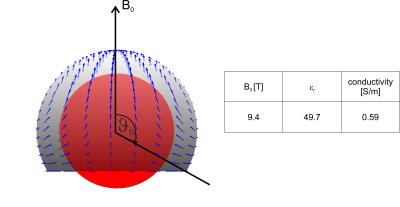
We let a surface current density flow on a spherical cap at a distance of 12.2 cm from the center of a homogeneous sphere (radius 9.2 cm) with opening angle ϑ0 (Fig. 1). Average tissue properties at 9.4 T were taken from (3) and are listed in Fig. 1. At the boundary (ϑ=ϑ0), we enforced the ϑ-component of the current to be zero and for ϑ>ϑ0 all current components were zero. For the divergence-free current patterns we used vector spherical harmonics (VSH) $$$\mathbf{X}^m_{\mu_k }$$$of non-integer degree μk and integer order m (0<m<μk):
$$\mathbf{X}^m_{\mu_k }=-i\left(\mathbf{r}\times\nabla\right)P^m_{\mu_k}(\cos\vartheta)\exp(im\varphi) $$
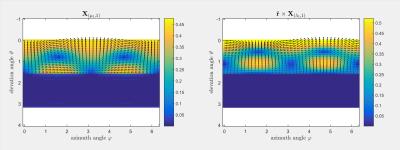
The fractional degree μk is the k-th root of the equation $$$P^m_{\mu}(\cos\vartheta_0)=0$$$. The term $$$P^m_{\mu}$$$ is the Legendre function of the first kind and can be understood as a generalization of the associated Legendre polynomials. For the curl-free current patterns we used vector spherical harmonics $$$\hat{\mathbf{r}}\times\mathbf{X}^m_{\lambda_k }$$$. The fractional degree λk (0<m<λk) is the k-th root of the equation $$$\frac{d}{d\vartheta}P^m_{\lambda}(\cos\vartheta_0)=0$$$. In Fig. 2 we show exemplary current patterns for m=1 and k=1 and an opening angle ϑ0 of 91°.
In order to calculate the electromagnetic fields excited by the spherical cap surface current distribution inside the spherical phantom, the framework of dyadic Green’s functions was applied (4,5). Therefore a series expansion of the non-integer VSH in terms of the standard, integer VSH is needed:
\begin{matrix}\mathbf{X}^m_{\mu_k}(\vartheta,\varphi) & =&\sum_{l=1}^\infty\alpha_l(m)\mathbf{X}^m_l(\vartheta,\varphi) \\\hat{\mathbf{r}}\times \mathbf{X}^m_{\lambda_k}(\vartheta,\varphi) & = & \sum_{l=1}^\infty\beta_l(m)\mathbf{X}^m_l(\vartheta,\varphi)+\gamma_l(m)\hat{\mathbf{r}}\times \mathbf{X}^m_l(\vartheta,\varphi)\\ \end{matrix}
The expansion coefficients α,β and γ can be obtained from the spherical harmonic transform. UISNR was evaluated according to the definition of equation 6 in (6).
Results
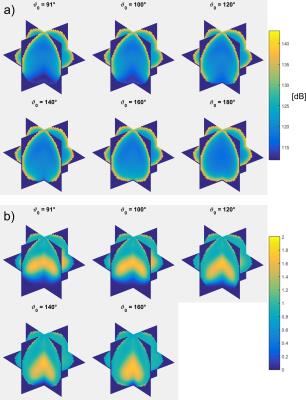
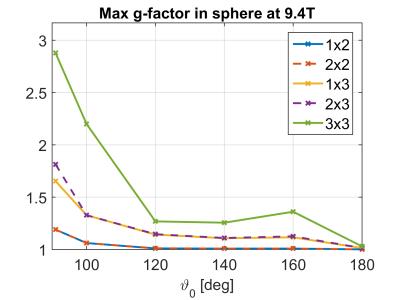
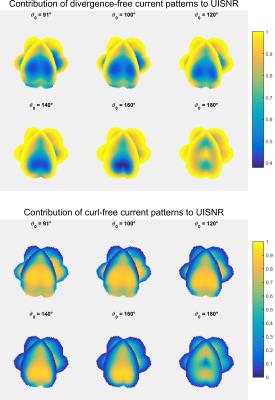
Figure 3a shows the spatial distribution of the UISNR for different opening angles. As expected, the smaller the opening angle ϑ0, the more the UISNR is decreased at the pole (ϑ=180°). However, in Fig. 3b it is demonstrated, that there is also an area, where UISNR is increased with respect to the completely symmetric case of ϑ0=180°. The influence of the opening angle on parallel imaging performance is shown in Fig. 4. For all acceleration factors, the g-factor penalty is minimal, when the current is allowed to flow on the entire sphere. However, it is interesting, that the g-factor penalty increases dramatically when ϑ0 <120° and is more or less constant within the range 120°<ϑ0<160° (except for 3x3 acceleration). Finally, we illustrate the contribution of divergence-free and curl-free current patterns to unaccelerated UISNR in Fig. 5. Divergence-free current patterns have a large contribution in the periphery, which is covered by the spherical cap. Except for the totally symmetric case of ϑ0=180°, there are signal voids in the inner regions. Curl-free current patterns behave exactly the opposite way, resulting in large contributions within the inner regions (ϑ0<180°).Discussion
Constraining the current to flow on a spherical cap of opening angle ϑ0<180°, redistributes the degrees of freedom of the underlying UISNR optimization problem from the entire spherical surface to a spherical cap. As a result, UISNR at the southern pole is tremendously decreased (no current can be optimized in this region). In contrast, central UISNR of a spherical cap surface current distribution is between 62% and 77% higher than for the entirely closed setup (Fig. 3b). Consequently, RF receive elements (=degrees of freedom) should be concentrated around the region of interest. Constraining the current to a spherical cap affects the contribution of curl-free and divergence-free current patterns to UISNR. Unlike the totally symmetric case (ϑ0=180°), curl-free elements have the major contribution in the central region of the sphere for ϑ0<180°. Generally speaking, the smaller the opening angle ϑ0, the more important the contribution of curl-free current patterns becomes.Conclusion
For the first time, the effect of an open-pole surface current distribution on UISNR and the contribution of curl-free and divergence-free current patterns was analyzed in a homogeneous spherical phantom. In future work, the homogenous sphere will be replaced by a realistic human body model.Acknowledgements
No acknowledgement found.References
(1) Pfrommer A. Proc 23rd ISMRM 2015, p. 856.
(2) Pfrommer A. Proc 24th ISMRM 2016, p. 175.
(3) Gabriel S. Phys Med Biol 41: p. 2271-2293, 1996.
(4) Tai C. Dyadic Green Functions in Electromagnetic Theory 2nd edition.
(5) Lattanzi R. MRM 68: p. 286-304, 2012.
(6) Lattanzi R. NMR in Biomed 23: p.142-151, 2010.
Figures