0723
In vivo observation and interpretation of time dependent diffusion in human gray matter1Radiology, New York University School of Medicine, Center for Biomedical Imaging, New York, NY, United States
Synopsis
The temporal scaling of the diffusion coefficient and diffusional kurtosis may reveal the underlying microstructural features of the human brain. Here we demonstrate time-dependent diffusion coefficient and kurtosis in gray matter areas of the human brain in vivo. Our results suggest that the major contribution of time-dependence in gray matter originates from intra-neurite water with the main source of restrictions, e.g. dentrites and beads, being short-range disordered in their placement.
Purpose
Time-dependent diffusion [1] is sensitive to the salient microstructural features of the brain. Here, we seek to determine if a time-dependent diffusion coefficient and kurtosis can be observed in human gray matter on a clinical scanner and provide a biophysical interpretation of its time-dependence.
Introduction
Diffusion in biological tissues is non-Gaussian, reflected by both a time-dependent diffusion coefficient [2,3] and non-zero diffusional kurtosis [1,3]. Previous works have reported on the time-dependence of the diffusion coefficient in brain white [4,5] and gray [2,6,7] matter. In this work we report on preliminary measurements of the time-dependence of the diffusion coefficient and diffusional kurtosis in cortical and deep GM areas of the human brain.Theory
Structural fluctuations in disordered systems manifest themselves in the temporal scaling of the instantaneous diffusion coefficient resulting in long time tails as [2]:
$$$D_{\mathrm{inst}}(t)\simeq D_{\infty} + \mathrm{const}\cdot t^{-\vartheta}\quad(1)$$$.
In Eq. 1, $$$\vartheta$$$ is the dynamical exponent related to the structural exponent $$$p$$$ as $$$\vartheta=\frac{p+d}{2}$$$, in $$$d$$$ spatial dimensions. In general the exponent $$$p$$$ depends on the structural correlations of the underlying geometry. The value $$$p=0$$$ corresponds to “conventionally” random (short-range disordered) geometries characterized by finite correlation length, while $$$p>0$$$ corresponds to hyperuniform (more-ordered) placement of restrictions, with suppressed structural fluctuations [8]. At long times, the power-law “tails” in diffusion coefficient and kurtosis are expected [2,3]. Diffusional kurtosis therefore may be used to probe for the underlying structure. Here, we apply it to GM areas of the human brain.
Methods
Four healthy subjects (1 female and 3 males) were scanned using a 3T Prisma (Siemens) scanner using a standard PG Spin Echo sequence along 64 directions in total and b values ranging from $$$b=$$$ 0.1, 0.4, 1.0 and 1.5 $$$\mathrm{ms/\mu m^2}$$$. Ten diffusion times, $$$\Delta$$$, were measured for each subject ranging from 21-100ms, probing length scales from 12-26 $$$\mu m$$$. Other sequence parameters were: $$$TE=$$$150ms, $$$TR=$$$4s, $$$\delta= 15$$$ms, with isotropic voxels $$$(2\mathrm{mm})^3$$$. For each subject, the $$$b_0$$$ images were registered to the subject’s MPrage image, to extract cerebral cortex and thalamus ROIs from FreeSurfer segmentation.Results/Discussion
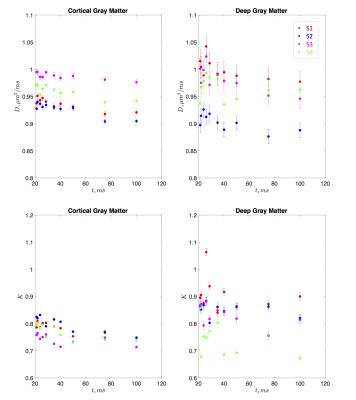
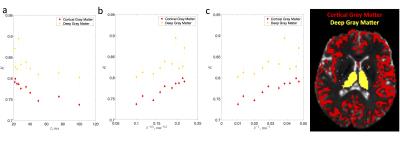
Both the diffusion coefficient and kurtosis were found to pronouncedly depend on time. Fig. 1 shows the time-dependence of the mean diffusivity and mean diffusional kurtosis, of the cortical and deep gray matter areas (ROIs shown in Fig. 2) among the four subjects. The diffusion coefficient in both ROIs appears to be time dependent, perhaps due to dendritic spines and beads along the intra-axonal space which occur at length scales of approximately $$$5 \mu m$$$ [9]. Kurtosis appears to have a more pronounced relative change of the order of 6% compared to the diffusion coefficient of 3%, over the measured time-scales. Fig. 2 highlights the time dependent diffusional kurtosis averaged over all subjects. The cortical gray matter appears to have slightly more pronounced time dependence as shown in Fig. 2a.
The power-law tail of the time-dependent kurtosis is then used to gain insight of the underlying microstructure. Fig. 2b-c shows kurtosis as a function of $$$t^{-1/2}$$$ and $$$t^{-1}$$$. Goodness of fit using the $$$\chi^2$$$ was implemented and showed slightly lower values for $$$\vartheta=1/2$$$ compared to $$$\vartheta=1$$$ indicating an observed dynamical exponent $$$\vartheta \simeq 0.5$$$. For the cortex $$$\chi^2/\nu\vert_{1/2}=4.15$$$ and $$$\chi^2/\nu\vert_{1}=4.18$$$ whereas for deep GM $$$\chi^2/\nu\vert_{1/2}=2.50$$$ and $$$\chi^2/\nu\vert_{1}=2.53$$$. Similarly, slightly higher correlation coefficients $$$\rho$$$ were found for $$$\vartheta=1/2$$$ compared to $$$\vartheta=1$$$. For the cortex $$$\rho_{1/2}=0.94$$$ and $$$\rho_{1}=0.93$$$ whereas for deep GM $$$\rho_{1/2}=0.64$$$ and $$$\rho_{1}=0.63$$$. If further confirmed, this scaling would be consistent with a dynamical exponent of $$$\vartheta=1/2$$$ identified in [2] in rat cortical GM OGSE measurements [7]. This observation would point to short-ranged disordered placement of restrictions along the $$$d=1$$$ dimensional neurites, e.g. dendrtitic spines and beads, consistent with histology [9] and confirming that the major contribution to the time-dependence of diffusivity and kurtosis originates from the intra-neurite water. Since the extra-neurite volume fraction was suggested to be on average 20% [10], our results indeed confirm that the observed time-dependence emerges predominately from the intra-neurite space.
Conclusions
This work presents preliminary data of time-dependence in the diffusion coefficient and kurtosis in human GM. Our data suggests that the scaling of diffusional kurtosis in cortical and deep GM may originate from short-ranged disordered dendritic spines and beads in the intra-neurite space.Acknowledgements
The authors acknowledge Thorsten Feiweier from Siemens Healthcare. Jelle Veraart, Hong-Hsi Lee, Benjamin Ades-aron and Gregory Lemberskiy for useful discussions about the data. Research was supported by the Fellowship from Raymond and Beverly Sackler Laboratories for Convergence of Physical, Engineering and Biomedical Sciences, by the Litwin Foundation for Alzheimer’s Research, by the NIH/NINDS award R01NS088040.References
1. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., & Kaczynski, K. (2005). Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 53(6), 1432-1440.
2. Novikov, D. S., Jensen, J. H., Helpern, J. A., & Fieremans, E. (2014). Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences, 111(14), 5088-5093.
3. Novikov, D. S., & Kiselev, V. G. (2010). Effective medium theory of a diffusion-weighted signal. NMR in Biomedicine, 23(7), 682-697.
4. De Santis, S., Jones, D. K., & Roebroeck, A. (2016). Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage, 130, 91-103.
5. Fieremans, E., Burcaw, L. M., Lee, H. H., Lemberskiy, G., Veraart, J., & Novikov, D. S. (2016). In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. NeuroImage, 129, 414-427.
6. Pyatigorskaya, N., Bihan, D., Reynaud, O., & Ciobanu, L. (2014). Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 tesla in the healthy rat brain cortex. Magnetic resonance in medicine, 72(2), 492-500.
7. Does, M. D., Parsons, E. C., & Gore, J. C. (2003). Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magnetic resonance in medicine, 49(2), 206-215.
8. Torquato, S., & Stillinger, F. H. (2003). Local density fluctuations, hyperuniformity, and order metrics. Physical Review E, 68(4), 041113.
9. Shepherd, G. M., Raastad, M., & Andersen, P. (2002). General and variable features of varicosity spacing along unmyelinated axons in the hippocampus and cerebellum. Proceedings of the National Academy of Sciences, 99(9), 6340-6345.
10. Syková, E., & Nicholson, C. (2008). Diffusion in brain extracellular space. Physiological reviews, 88(4), 1277-1340.
Figures