0722
Validation of DTI-based parcellation of the thalamus in the squirrel monkey1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Institute of Imaging Science, Vanderbilt University, Nashville, TN, United States, 3Psychological Sciences, Vanderbilt University, 4Electrical Engineering, Vanderbilt University, 5Biomedical Engineering, Vanderbilt University
Synopsis
DTI has been used to noninvasively resolve major thalamic nuclei using an unsupervised clustering algorithm. However, rigorous validation of the method has not been studied. Here, we evaluated the method by comparing the parcellation results with histology in the same non-human primate. We found that some nuclei were clustered with larger differences from histology. That probably was because the diffusion properties of these nuclei were not coherent. In addition, the pipeline constructed in this study is also a framework to validate other approaches for thalamic nuclei parcellation.
Introduction
Diffusion tensor imaging (DTI) has been used to noninvasively resolve major thalamic nuclei using an unsupervised clustering algorithm1. However, rigorous validation of the DTI-based parcellation in the thalamus has not been studied. Here, we evaluate the method by comparing the parcellation results with histology in the same non-human primate.Method
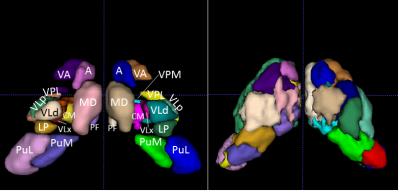
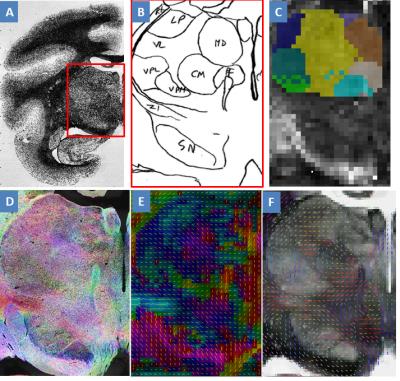
Histological nucleus definition: A squirrel monkey brain was frozen and sectioned coronally at 50μm thickness using a microtome. The tissue blockface was photographed after every three sections to compose an intermediate space for registration from microscopy space to DTI space. Every sixth section was reacted for Acetylcholinesterase (AChE) and photographed under a light microscope with 0.5X magnification. The borders of primary thalamic nuclei, 14 for either side of the thalamus, were identified by an expert, based on architectonics revealed by the AChE stain2. Each thalamic nucleus was then transformed to DTI space using deformation fields calculated via a modified multi-step registration procedure from light microscopy to DTI space3,4. The 14 thalamic nuclei are the Pulvinar inferior (PuI), Pulvinar medial (PuM), Pulvinar lateral (PuL), Ventral posterolateral (VPL), Ventral posteromedial (VPM), Centromedian (CM), Parafascicular (PF), Anterior (A), Ventral anterior (VA), Media dorsal (MD), Ventrolateral posterior (VLp), Ventrolateral medial (VLx), Ventrolateral dorsal (VLd) and Lateral posterior (LP) nucleus. In addition, another series of tissue sections were stained for myelin.
DTI parcellation: Before sectioning, the fixed monkey brain was scanned (3D EPI sequence, shots=4, TR=410ms, TE=41ms, number of gradient directions=101, b≈3000s/mm2, voxel size=0.3mm×0.3mm×0.3 mm, data matrix=128×192×128, b=0 with normal and reversed PE) using a 9.4Tesla scanner. FSL TOPUP5 and EDDY6 were used to correct eddy current distortion as well as movement, and the FSL diffusion tookit was used to estimate the diffusion tensor in thalamic nuclei. A K-means clustering algorithm in MATLAB was modified to cluster thalamic nuclei (k=14) for each hemisphere. The distance metric used in the modified k-means between voxels was defined as a linear combination of the Mahalanobis voxel distance and the Frobenius tensor distance (see Wiegell et al1 for more details). The cluster centroids for k-means were initialized by the center of mass for each histological nucleus.
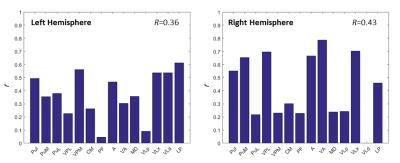
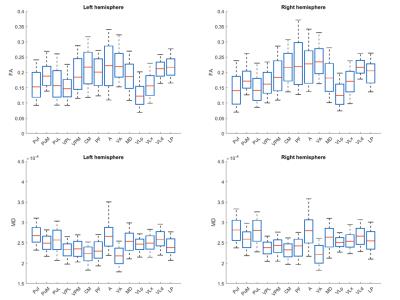
Comparison of DTI and histology: To evaluate overall accuracy of parcellation, we calculated the Jaccard index for all nuclei, defined as R. To evaluate accuracy of each parcellated nucleus, we calculated the Jaccard index for each nucleus, defined as r. Both R and r indicate how many out of total number of voxels were correctly clustered. To further investigate how the diffusion properties distributed across the thalamic nuclei, we calculated the mean of fractional anisotropy (FA) and mean diffusivity (MD) for each nucleus. Moreover, structure tensor analysis7 was performed on one micrograph of myelin stained tissue slice. The derived histological tensor was compared with diffusion tensor in micrograph space, in terms of primary eigenvector.
Results
Figure 1A shows the histological nuclei in the thalamus and figure 1B shows the k-means clustering results. Figure 2 displays the Jaccard index of every parcel r and the Jaccard index of overall parcellation R. Figure 3 illustrates FA and MD of each thalamic nucleus. Figure 4 gives an example of comparison between thalamic parcellation and histology.
Conclusion and Discussion
This study compared the DTI-based parcellated thalamic nuclei with histologically identified nuclei in the same monkey for the first time. Figure 2 indicates good agreement between clustering and histology for some thalamic nuclei. However, some nuclei were segregated with larger differences from histology. That probably was because the diffusion properties of these nuclei were not coherent enough (FA of PF in Figure 3, and MD in Figure 4). In addition, the pipeline constructed in this study is also a framework to validate other approaches for thalamic nuclei parcellation.Acknowledgements
No acknowledgement found.References
1. Wiegell MR, Tuch DS, Larsson HBW, Wedeen VJ. Automatic segmentation of thalamic nuclei from diffusion tensor magnetic resonance imaging. NeuroImage. 2003;19(2):391-401.
2. Stepniewska I, Preuss TM, Kaas JH. Architectonic subdivisions of the motor thalamus of owl monkeys: Nissl, acetylcholinesterase, and cytochrome oxidase patterns. The Journal of Comparative Neurology. 1994;349(4):536-557.
3. Choe A, Gao Y, Li X, Compton K, Stepniewska I, Anderson A. Accuracy of image registration between MRI and light microscopy in the ex vivo brain. Magnetic Resonance Imaging. 2011;29(5):683-692.
4. Gao Y, Choe AS, Stepniewska I, Li X, Avison MJ, Anderson AW. Validation of DTI Tractography-Based Measures of Primary Motor Area Connectivity in the Squirrel Monkey Brain. PloS one. 2013;8(10):e75065.
5. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20(2):870-888.
6. Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063-1078.
7. Schilling K, Janev V, Gao Y, Stepniewska I, Landman B, Anderson A. Comparison of 3D orientation distribution functions measured with confocal microscopy and diffusion MRI. Neuroimage. 2016.
Figures