0705

Towards Glioma Grading Using Non-Gaussian Diffusion Imaging with a Continuous-time Random Walk Model and A Quantile Histogram Analysis

Muge Karaman¹, Jiaxuan Zhang^1,2, Zheng Zhong^1,3, Kejia Cai^1,4, Wenzhen Zhu², and Xiaohong Joe Zhou⁵

¹Center for MR Research, University of Illinois at Chicago, Chicago, IL, United States, ²Department of Radiology, Tongji Hospital, Tongji Medical College, Huazhong University of Science and Technology, People's Republic of China, ³Department of Bioengineering, Chicago, IL, United States, ⁴Department of Bioengineering, University of Illinois at Chicago, Chicago, IL, United States, ⁵Departments of Radiology, Neurosurgery, and Bioengineering, University of Illinois at Chicago, IL, United States

Synopsis

Gliomas are the most common primary tumors of the central nervous system. As surgical biopsy may not be always feasible, an accurate noninvasive glioma grading is highly desirable for planning treatments. Recently, a number of non-Gaussian diffusion models were developed to characterize the anomalous diffusion behavior of the complex biological tissue. Among these, the continuous-time random walk (CTRW) model showed a great potential to probe the tissue heterogeneity and complexity that is elevated with tumor progression. In this study, we show that the CTRW parameters are capable of differentiating glioma grades, beyond simply separating low-grade and high-grade as in many diffusion MR studies on gliomas.

Introduction

Gliomas are the most common primary brain tumors in adults, spanning from grade I to IV according to the 2016 WHO guidelines. Glioma grade is typically determined by invasive surgical biopsy followed by histopathology analysis. This approach, however, may not always be feasible due to considerable surgical risks. An accurate imaging-based noninvasive grading method is therefore needed. While many imaging methods have been proposed to differentiate between low- (I and II) and high-grade (III and IV) gliomas, these techniques have limited success in determining individual grades¹. For example, apparent diffusion coefficient (ADC) from the conventional mono-exponential model (i.e., a Gaussian model) has not been established as a tumor-grading marker, despite a large number of studies¹. Recently, a number of non-Gaussian diffusion models were developed and showed great potential to probe tumor microstructures and microenvironment^2-13. In this study, we demonstrate the feasibility of using a novel anomalous diffusion model, the continuous-time random walk (CTRW) model, combined with a quantile histogram analysis to differentiate Grade II (GrII), III (GrIII), and IV (GrIV) gliomas.

Methods

Patients: This study enrolled a total of 103 patients (45 females and 58 males; ages 10-75 years) with histopathologically proven gliomas, consisting of 2 patients with Grade I, 46 Grade II, 23 Grade III, and 32 Grade IV tumors according to the WHO guidelines. Grade I gliomas were excluded from the analysis because of an inadequate sample size.

Image acquisition: All patients were scanned on a 3T GE MR750 scanner with a 32-channel head coil. The MRI protocol included pre-/post-contrast T1, FSE T2, T2 FLAIR, and DWI with 17 b-values (0 to 4000 s/mm²). For DWI, the other acquisition parameters were: TR/TE=4700/100ms, slice thickness=5mm, Δ=38.6ms, δ=32.2ms, FOV=22cm×22cm, reconstruction matrix size=256×256, and total scan time~4 minutes. Trace-weighted images were obtained to minimize the effect of diffusion anisotropy.

Diffusion Analysis: The multi-b-value diffusion images were analyzed with the CTRW model¹¹, $$$S/S_0=E_α (-(bD_m )^β)$$$, where D_m is an anomalous diffusion coefficient, α and β are temporal and spatial diffusion heterogeneity parameters, respectively, and E_α is a Mittag-Leffler function. A least squares algorithm was used for nonlinear fitting.

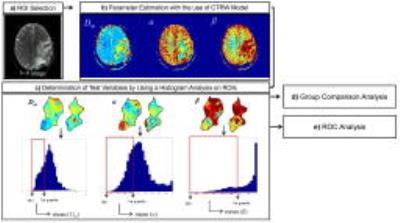
Statistical Analysis: The contrast-enhancing ROIs were drawn by two neuroradiologists jointly on b=0 images guided by other MRI images. A quantile histogram analysis, using the means of the first quartile of D_m, α, or β within the ROIs, was employed to determine the test variables for each patient. A Mann-Whitney U-test was used for the group comparison, followed by a receiver operating characteristic (ROC) analysis for differentiation among the grades. Figure 1 summarized the data analysis steps.

Results

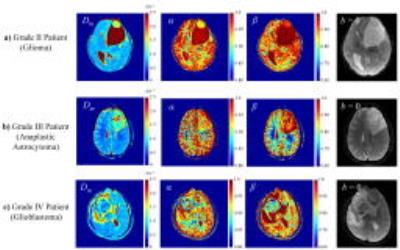
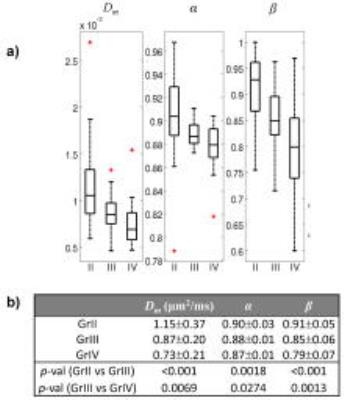
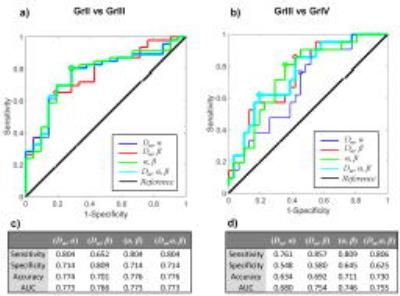
Figure 2 shows D_m, α, and β maps, as well as b=0 images, from a representative patient in each of the GrII, GrIII, and GrIV groups. The higher-grade tumors showed lower values in all three parameters than the lower-grade tumors. This observation was supported by the group analysis as presented in the boxplots of the mean D_m, α, and β (Fig. 3a), and by the statistical significance (p-values<0.05) of the difference between GrII and GrIII, as well as between GrIII and GrIV groups (Fig. 3b). Figure 4 shows the ROC results for different combinations of the CTRW parameters in differentiating GrII vs. GrIII (Fig. 5a) and GrIII vs. GrIV (Fig. 5b). The combinations of (α,β) and (D_m,α,β) yielded the highest sensitivity (0.804), specificity (0.714), accuracy (0.776) and area under the curve (AUC = 0.773) in differentiating GrII vs. GrIII gliomas. The (D_m,α,β) combination provided the highest accuracy (0.730) and AUC (0.755) while the (α,β) combination produced slightly better sensitivity (0.809 vs 0.806) and specificity (0.645 vs 0.625) in differentiating GrIII vs. GrIV gliomas.

Discussion and Conclusion

Our results based on more than 100 patients showed that the CTRW model has potential in differentiating GrII, GrIII, and GrIV gliomas. This represents an encouraging development from simply separating low-grade and high-grade as in the vast majority of diffusion MR studies. The quantile histogram analysis provides a “filter” for focusing on solid tumor regions without relying on precise ROI selections. This approach is built upon a justifiable assumption that lower D_m, α, and β regions are most relevant to tumor grading due to their sensitivity to diffusion restriction and/or heterogeneity¹¹. More importantly, this approach is also consistent with the current pathological practice of selecting the tissue from the worst part of the lesion. Using an ROC analysis, we have demonstrated that the combinations of the CTRW parameters are capable of differentiating glioma grades, pointing to a possible way for developing a non-invasive imaging-based glioma grading method without biopsies.

Acknowledgements

This work was supported in part by NIH 1S10RR028898, 3R01MH081019, and National Natural Science Foundation of China 81171308 and 81401389. We thank Drs. Keith R. Thulborn, Richard L. Magin, Karen Xie, Frederick C. Damen, Liping Qi, and Rong-Wen Tain for valuable discussions. Muge Karaman and Jiaxuan Zhang contributed equally to this work and share the first authorship.

References

[1] Maier SE, Sun Y, Mulkern RV. Diffusion imaging of brain tumors. NMR Biomed. 2010;23(7):849-864.

[2] Niendorf T, Dijkhuizen RM, Norris DG, et al. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn Reson Med. 1996;36(6):847-57.

[3] Bennett KM, Schmainda KM, Bennett R, et al. Characterization of continuously distributed cortical Water diffusion rates with a stretched-exponential model. Magn Reson Med. 2003;50:727-734.

[4] Yablonskiy Dam Bretthrst GL, Ackerman JJH. Statistical model for diffusion attenuated MR signal Magn Reson Med. 2003;50:664-669.

[5] Assaf y, Mayk A, Cohen Y. Displacement imaging of spinal cord using q-space diffusion-weighted MRI. Magn Reson Med. 2000;44:713-722.

[6] Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53:1432-1440.

[7] Magin RL, Abdullah O, Baleanu D, et al. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson Im. 2008;190:255–270.

[8] Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. 2010;63:562–569.

[9] Ingo C, Magin RL, Colon-Perez L, et al. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med. 2014;71(2):617–27.

[10] Sui Y, He W, Damen FW, Wanamaker C, Li Y, Zhou XJ. Differentiation of Low- and High- Grade Pediatric Brain Tumors with High b-Value Diffusion weighted MR Imaging and a Fractional Order Calculus Model. Radiology. 2015;277(2):489–496.

[11] Karaman MM, Sui Y, Wang H, et al. Differentiating low- and high-grade pediatric brain tumors using a continuous-time random-walk diffusion model at high b-values. Magn Reson Med. 2015; 76:1149-1157.

[12] Karaman MM, Wang H, Sui Y, et al. Fractional Motion Diffusion Model for Grading Pediatric Brain Tumors. Neuroimage Clin. 2016: 12:707-714.

[13] Fan Y, Gao JH. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys Rev E. 2015;92(1):012707.

Figures

Figure 1: Data analysis steps for individual patient (a-c) and for each tumor grade as a group (d,e). a) The contrast-enhancing ROIs were delineated on b=0 image with the help of conventional MR images. b) The CTRW parameters were determined. c) The histograms of D_m, α, and β within the ROIs and their first quartiles were obtained for the calculation of the means of the lower tails (25%). The mean parameter values were used for group comparison in d, and for ROC analysis to assess the performance of the CTRW parameters for differentiating GrII, GrIII, and GrIV gliomas in e.

Figure 2: Maps of D_m, α, and β as well as b=0 image from a representative patient in each of the GrII (top row), GrIII (middle row), and GrIV (bottom row) groups. The ROIs are shown with black contours in the CTRW parameter maps. The CTRW parameter values of the solid tumor regions within the ROIs decreased progressively as the tumor grade increased.

Figure 3: a) Boxplots of the mean values of the CTRW parameters (D_m, α, and β) from the lower tails (25%) of their histograms, and b) the corresponding descriptive statistics, showing sample mean and standard deviation, ($$$\bar{x}±σ$$$), of D_m, α, and β for GrII, GrIII, and GrIV glioma groups. All parameters decreased as the tumor grade increased, exhibiting significant differences (p-values<0.05) between GrII and GrIII as well as GrIII and GrIV glioma groups based on a Mann-Whitney U-test as listed in the last two rows.

Figure 4: The ROC curves of using the different combinations of D_m, α, and β for differentiating glioma grades. a): GrII vs. GrIII; b): GrIII vs. GrIV. Summary of the corresponding best cut-off sensitivity and specificity values (shown as circles in the curves) as well as the accuracy and the AUC for the ROC curves in a and b is given in c and d, respectively. The different combinations of the parameters were obtained by using a multivariate logistic regression algorithm.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0705