0686
Deep Convolutional Neural Network for Acceleration of Magnetic Resonance Angiography (MRA)1Yonsei University, Seoul, Korea, Republic of
Synopsis
In this paper, we propose a deep CNN with skip connection for reconstruction of highly undersampled MRA images. According to the experiments, the proposed method could restore most of fine vessel structures manifested in full-sampled MRA images.
Introduction
Magnetic resonance angiography (MRA) requires considerable time because it needs to acquire multi-slice images. To reduce the acquisition time, several reconstruction methods have been proposed. One representative method is compressed-sensing (CS)-based optimization method which uses the sparsity of the magnetic resonance (MR) images by transforming images to specific domains [1]. However, CS has limits in recovering fine structures of highly under-sampled MR images. In computer vision, convolutional neural network (CNN)-based reconstruction methods have been proposed and used for various tasks in optical images, for instance, super resolution and artifacts removal [2-3]. Moreover, recently, there have been attempts to apply CNN for reconstruction of undersampled MR images [4]. However, because they also have limits in restoring many of detailed structures, it is not suitable for reconstruction of MRA images which contains many detailed vessel structures. In this study, we propose very deep (25-layer) CNN with skip connection layer for reconstruction of undersampled MRA images to restore more of detailed vessels.Theory and methods
The proposed method is depicted in figure 1. The first layer of the proposed deep CNN is can be expressed as,$$ G_1 = max(0,W_1*x+b_1)$$ where $$$\normalsize x$$$ is input, $$$\normalsize W_1$$$ and $$$\normalsize b_1$$$ are filters and biases. The size of $$$\normalsize W_1$$$ is $$$\normalsize k_1\times k_1 \times m_1$$$. After convolution between $$$\normalsize W_1$$$ and $$$\normalsize x$$$, rectified linear unit (ReLu, $$$\normalsize max(0,x)$$$) is used for nonlinear activation. After the first layer, the $$$\normalsize n$$$th $$$\normalsize (n\geq2)$$$ layer is expressed as,$$ G_n = max(0,W_n*G_n-1+b_n)$$ where the size of $$$\normalsize W_n$$$ is $$$\normalsize k_n\times k_n \times m_n$$$. The $$$\normalsize N$$$th layer is expressed as,$$ G_N = W_{N-1}*G_{N-1}+b_{N}$$where the size of $$$\normalsize W_n$$$ is $$$\normalsize k_N\times k_N \times 1$$$. After $$$\normalsize N$$$th convolution layer, summation layer sums the output of the $$$\normalsize N$$$th convolution layer and the input. This summation layer makes the network to train the residual of the output and input image. To train the network, the l2 difference between the true high-resolution image and network output is used as the loss function. The loss function is defined as,$$l(\Theta)= \frac{1}{M}\sum_{i=1}^M\parallel G(x_i;\Theta)-y_i\parallel^2$$where $$$\normalsize M$$$ is the number of data sets, $$$\normalsize y$$$ is the true image, $$$\normalsize G(x;\Theta)$$$ is output image of the network, and $$$\normalsize \Theta=\{(W_1,b_1),...,(W_n,b_n),...,(W_N,b_N)\}$$$. In contrast to the conventional CNN-based methods, the original MR data in the k-space is used for reconstruction. When the network output image is acquired, the sampled part of its k-space is replaced with the originally acquired k-space data [5]. This can be described by,$$K_R(k_x,k_y)=\left\{ \begin{array}{ll} K_O(k_x,k_y) &, ~{\rm if}~ (k_x,k_y)\notin S \\ K_N(k_x,k_y) &, ~{\rm if}~ (k_x,k_y)\in S\\\end{array} \right.$$where $$$\normalsize K_R$$$ denotes the k-space of the desired reconstructed image, $$$\normalsize K_O$$$ is the original k-space, $$$\normalsize K_N$$$ represents the k-space of the network output image, and $$$\normalsize S$$$ denotes the sampling location of the k-space. The reconstructed image is then acquired using inverse Fourier transform of $$$\normalsize K_R$$$. After passing through deep CNN, under-sampled magnetic resoance angiography (MRA) multi-slice images are reconstructed to the high-resolution images with fewer artifacts. Then, high-resolution final angiography image is acquired by maximum image projection of the reconstructed MRA multi-slice images.
We used 600 MRA images from Information eXtraction from Images sites (IXI) [6]. Among 600 images, 500 images were used for training data set and 100 images were used for test data set. In deep CNN, we used parameters as follows: patch size $$$\normalsize 61\times61$$$, number of layers $$$\normalsize N=25$$$, kernel size $$$\normalsize k_n=3$$$, and number of filters for each convolution layer $$$\normalsize m_n=64$$$. Training required about 12 hours to complete using an Intel i7-4790 3.60 GHz CPU, GeForce GTX 1080, and 32 G memory.
Results
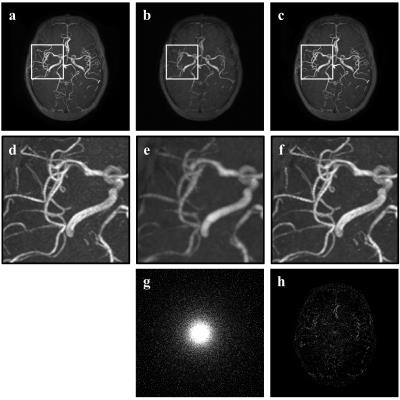
Fig. 2 shows the original and restored MRA images with acceleration factor 5.5 by 2D Cartesian sampling pattern. According to Fig. 2 d-f, proposed method restores fine structures of blood vessel while zero padding image lost much information and shows blur artifacts. Fig. 3 shows the original and restored MRA images with acceleration factor 11 by 2D Poisson sampling pattern. According to Fig. 3d-f, even in high acceleration factor, proposed method restores fine structures and remove artifacts. The difference image in Fig. 2h and Fig. 3h between true image and proposed one show that proposed method recovers almost the whole blood vessels from highly under-sampled image.Conclusion
In this paper, we propose a deep CNN with skip connection for reconstruction of highly undersampled MRA images. According to the experiments, the proposed method could restore most of fine vessel structures manifested in full-sampled MRA images.Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2016R1A2B4015016).References
[1] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.
[2] Dong, Chao, et al. "Learning a deep convolutional network for image super-resolution." European Conference on Computer Vision. Springer International Publishing, 2014.
[3] Dong, Chao, et al. "Compression artifacts reduction by a deep convolutional network." Proceedings of the IEEE International Conference on Computer Vision. 2015.
[4] Wang, Shanshan, et al. "Accelerating magnetic resonance imaging via deep learning." Biomedical Imaging (ISBI), 2016 IEEE 13th International Symposium on. IEEE, 2016.
[5] Ravishankar, Saiprasad, and Yoram Bresler. "MR image reconstruction from highly undersampled k-space data by dictionary learning." IEEE transactions on medical imaging 30.5 (2011): 1028-1041.
[6] Information eXtraction from Images sites (IXI). http://brain-development.org/ixi-dataset/. Accessed October 1, 2016.
Figures
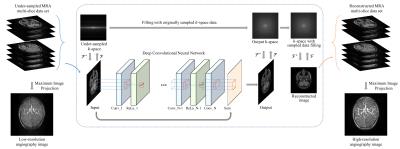
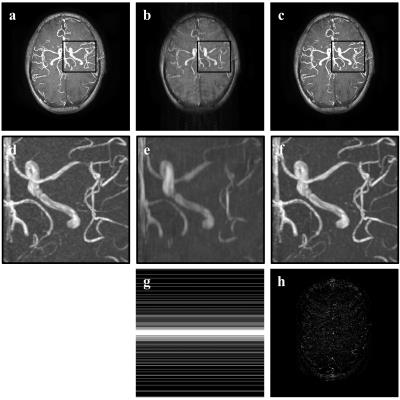
Fig.2 Reconsturcted MRA image with 2D Cartesian 5.5 acceleration factor (a) true image, (b) zero-padding image, (c) proposed image, (d) magnified image of (a), (e) magnified image of (b), (f) magnified image of (c), (g) 2D Cartesian sampling pattern, (h) difference image between (a) and (c)