0644

On the Influence of Sampling Pattern Design on Deep Learning-Based MRI Reconstruction
Kerstin Hammernik1, Florian Knoll2,3, Daniel K Sodickson2,3, and Thomas Pock1,4

1Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria, 2Center for Biomedical Imaging and Center for Advanced Imaging Innovation and Research (CAI2R), NYU School of Medicine, New York, NY, United States, 3Department of Radiology, NYU School of Medicine, New York, NY, United States, 4Safety & Security Department, AIT Austrian Institute of Technology GmbH, Vienna, Austria

Synopsis

In this work, we address the question if variable density sampling of 2D Cartesian knee sequences can improve deep learning-based MRI reconstruction. Our results suggest that incoherent artifacts introduced by variable density sampling are beneficial to reconstruct highly accelerated sequences. Additionally, we show that our learning-based approach for regular sampling improves reconstruction results compared to classical compressed sensing methods with variable density sampling for our target application.

Purpose

The fundamental principles of compressed sensing (CS) rely on incoherent undersampling artifacts which can be realized with radial$$$^1$$$, spiral or random sampling patterns$$$^{2}$$$. However, many clinical routine exams are still based on 2D Cartesian regular sampling. To overcome the limitations of CS methods for Cartesian sampling, a deep learning approach that learns a network for efficient reconstruction of 2D Cartesian sequences was recently proposed$$$^3$$$. In this work, we target the open question if learning-based approaches actually benefit from structured undersampling artifacts due to regular sampling or if they perform better with incoherent undersampling artifacts like CS methods.

Methods

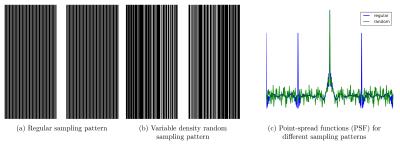
Many clinical protocols use a regular sampling scheme with fully-sampled k-space center to estimate coil sensitivity profiles (see Figure 1a). However, this sampling scheme leads to characteristic backfolding artifacts illustrated by the point-spread function (PSF) in Figure 1c. Using a variable density sampling pattern (Figure 1b) that has the same fully-sampled k-space center and the same amount of phase encoding steps as the regular sampling scheme introduces more incoherent artifacts (Figure 1c). The variable density sampling pattern is generated according to Lustig et al$$$^1$$$.

In order to perform retrospective downsampling experiments, we obtain fully-sampled data from 10 patients part of a study approved by the IRB using a clinical 3T system (Skyra, Siemens Healthineers) and a 15-channel knee coil. We acquire the following sequences: Proton density weighted (PD) coronal scans with sequence parameters TR=2800ms, TE=27ms, TF=4, matrix size 320x288 and PD with fat saturation (FS) coronal scans with sequence parameters TR=2870, TE=33ms, TF=4, matrix size 320x288. We train individual variational networks$$$^3$$$ using regular and variable density random sampling patterns for acceleration factors $$$R\in\{3,4\}$$$ on 100 slices from 5 patients. The network architecture consists of 10 gradient descent steps. In each of these steps, we learn the regularization term that consists of 48 filter kernels of size $$$11\times 11$$$ along with their corresponding activation functions and the regularization parameter that balances between data fidelity and regularization term. The network architecture is trained to minimize the mean-squared error (MSE). Testing is performed on the remaining 5 patients resulting in a total of 160 slices for PD and 148 slices for FS.

As a reference parallel imaging combined CS method (PI-CS), we use Total Generalized Variation (TGV) reconstruction$$$^4$$$. All regularization parameters are individually selected for each contrast, acceleration factor and sampling pattern such that the results minimize the MSE.

Results

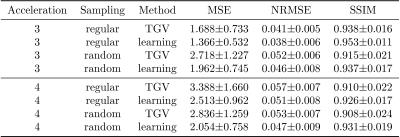
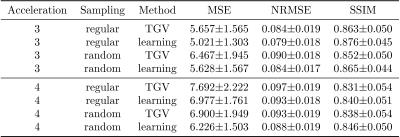
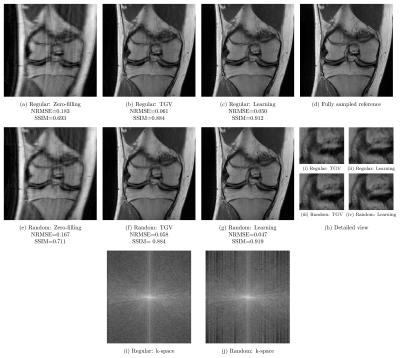
We report quantitative results in terms of the MSE, normalized root-mean squared error (NRMSE) and Structural Similarity Index (SSIM) for PD in Figure 2 and FS in Figure 3. Both sequences show the same behavior: Regular sampling outperforms variable density random sampling for $$$R=3$$$ in terms of all quantification measures. The introduced randomness improves the reconstruction results for both PI-CS TGV and our learned network for $$$R=4$$$.

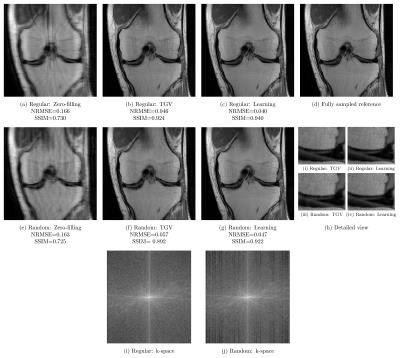
Qualitative results for a PD scan are illustrated for $$$R=3$$$ in Figure 4 and $$$R=4$$$ in Figure 5. These results verify the previous observations: For acceleration factor $$$R=3$$$, results based on regular sampling appear sharper. The k-space of regular sampling verifies the improved reconstruction quality: The k-space for regularly sampled network reconstruction in Figure 4i appears homogeneous, while the k-space for randomly sampled network reconstruction results shows inhomogeneities where larger gaps are present (Figure 4j). Results for $$$R=4$$$ illustrated in Figure 5 indicate the improved reconstruction quality of randomly sampled data. The variational network reconstructions appear sharper and more natural compared to the PI-CS method in all cases. Additionally, our networks learned for regular sampling $$$R=4$$$ outperform (PD) and are on par (FS) with TGV for variable density random sampling $$$R=4$$$. Figure 5i and Figure 5j show the k-spaces of the regularly and randomly sampled network reconstructions.

Discussion and Conclusion

Our results on 2D Cartesian knee sequences show that incoherent undersampling artifacts introduced by variable density sampling are beneficial for acceleration factor $$$R=4$$$. For acceleration factor $$$R=3$$$, our results indicate that regular sampling improves the results for both PI-CS and deep learning-based approaches, verified by the homogeneously filled k-space. Surprisingly, the PI-CS results also show better performance for regular sampling for this specific sequence- and hardware setting. Our hypothesis is that the PI component is the dominant element in this case. Our deep learning approach outperforms PI-CS in terms of quantitative results (MSE, NRMSE and SSIM) as well as qualitative results. For $$$R=4$$$, the network reconstructions based on regular sampling are superior compared to the PI-CS reconstructions with variable density sampling.

Acknowledgements

We acknowledge grant support from the Austrian Science Fund (FWF) under the START project BIVISION, No. Y729, NIH P41 EB017183, NIH R01 EB000447 and NVIDIA corporation.

References

1. K. T. Block, M. Uecker, J. Frahm, “Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint”, Magn Reson Med, vol. 57, no. 6, pp. 1086–1098, 2007.

2. M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging”, Magn Reson Med, vol. 58, no. 6, pp. 1182–1195, 2007.

4. K. Hammernik, F. Knoll, D. K. Sodickson, and T. Pock, “Learning a Variational Model for Compressed Sensing MRI Reconstruction”, in Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2016, no. 24, p. 1088.

5. F. Knoll, K. Bredies, T. Pock, and R. Stollberger, “Second order total generalized variation (TGV) for MRI”, Magn Reson Med, vol. 65, no. 2, pp. 480–491, 2011.

Figures

Figure 1: (a) shows a regular (clinical) sampling pattern. The k-space center and the number of reference lines in the variable density random sampling pattern (b) are equal to (a). Using regular sampling results in backfolding artifacts, depicted by the blue point-spread function (PSF) in plot (c). Using the variable density random sampling pattern introduces more incoherent artifacts, depicted by the green PSF.

Figure 2: Quantitative comparison of regular sampling and variable density random sampling: We compare 160 slices of coronal proton density (PD) scans in terms of the mean-squared error (MSE), normalized root-mean squared error (NRMSE) and structural similarity index (SSIM). The learning-based approach yields superior results than the PI-CS TGV approach in all cases. For acceleration factor $$$R=3$$$, variable density random sampling performs worse than regular sampling also for TGV. Variable density sampling improves the results for acceleration factor $$$R=4$$$.

Figure 3: Quantitative comparison of regular sampling and variable density random sampling: We compare 148 slices of coronal fat-saturated proton density (FS) scans in terms of the mean-squared error (MSE), normalized root-mean squared error (NRMSE) and structural similarity index (SSIM). The learning-based approach yields superior results than the PI-CS TGV approach in all cases. For acceleration factor $$$R=3$$$, variable density sampling performs worse than regular sampling also for TGV. Variable density random sampling improves the results for acceleration factor $$$R=4$$$.

Figure 4: Qualitative comparison of regular sampling and variable density random sampling for a selected coronal PD slice and acceleration factor $$$R=3$$$. The detailed view illustrates that the learned variational network results appear sharper compared to TGV. For this acceleration factor, the randomly sampled results appear blurrier compared to regularly sampled results which can best be seen in the detailed view. This is also verified by the homogeneous k-space of the regularly sampled network reconstruction result depicted in (i).

Figure 5: Qualitative comparison of regular sampling and variable density random sampling for a selected coronal PD slice and acceleration factor $$$R=4$$$. The variable density sampling clearly improves reconstruction quality for all cases. The k-spaces for the network reconstructions are illustrated in (i) and (j).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0644