0640

Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation
Bo Zhu1,2,3, Jeremiah Z. Liu1,4, Bruce R. Rosen1,2, and Matthew S. Rosen1,2,3

1A.A. Martinos Center for Biomedical Imaging, Dept. of Radiology, Massachusetts General Hospital, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Dept. of Physics, Harvard University, Cambridge, MA, United States, 4Department of Biostatistics, Harvard University, Boston, MA, United States

Synopsis

It has been widely observed that real-world data presented in high dimensional space tend to lie along a nonlinear manifold with much lower dimensionality. The reduced dimensionality manifold captures intrinsic data properties such as sparsity in a transform domain. We describe here an automated neural network framework that exploits the universal function approximation of multilayer perceptron regression and the manifold learning properties demonstrated by autoencoders to enable a new robust generalized reconstruction methodology. We demonstrate this approach over a variety of MR image acquisition strategies, showing excellent immunity to noise and acquisition artifacts.

Introduction

We describe here an automated neural network framework that exploits the universal function approximation of multilayer perceptron regression [1] and the manifold learning properties demonstrated by autoencoders [2] to enable a new robust generalized reconstruction methodology. We demonstrate this approach over a variety of MR image acquisition strategies.

Theoretical motivation and reconstruction framework

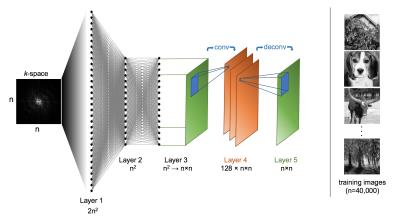
Real-world data presented in high dimensional space $$${C}^{n^{2}}$$$ tend to lie along a nonlinear manifold $$$M$$$ with much lower dimensionality $$$d_{M}$$$ [3]. The reduced dimensionality manifold captures intrinsic data properties such as sparsity in a transform domain. An image reconstruction technique conditioned upon this manifold would be more robust to non-imagelike corruption such as noise, undersampling, and the effects of imperfect acquisition processes such as phase distortion. Inspired by denoising autoencoders, which have been demonstrated to automatically learn such manifolds by encoding a compressed latent representation of image data, we have developed a neural network architecture for image reconstruction that maps k-space to image space utilizing the universal approximation theorem. In this usage, AUTOMAP (AUtomated TransfOrm by Manifold APproximation) optimizes a reconstruction function for any MR acquisition setup by a trained mapping between input-output pairs $$$\left ( x_{i}, y_{i}\right )$$$ corresponding to time-domain k-space samples and their ideal image representations. The selection of input-output training pairs and how they are generated depends upon the desired application. The AUTOMAP neural network architecture is composed of fully-connected layers followed by a convolutional autoencoder (Figure 1). The primary function of the fully-connected layers is to perform nonlinear regression mapping k-space and to the image domain, and the convolutional autoencoder further enforces an image-like manifold constraint on the reconstruction.

Methods and experiments

We trained AUTOMAP to learn an optimal feedforward reconstruction network between corrupted k-space and image space for two different acquisition scenarios: A) noisy variable-density spiral and B) imperfectly aligned EPI trajectory. In order to demonstrate the out-of-sample generalization capabilities of AUTOMAP training, the data for our training set is composed entirely of photographs of natural scenes downloaded from IMAGENET [4]; for each acquisition, the system was not exposed to any MR or other medical images until validation.

The training corpus is comprised of 40,000 photographs from IMAGENET cropped to 128x128. Each image was Fourier Transformed into A) variable-density 10-interleave spiral k-space by NUFFT [5] and further corrupted by additive Gaussian noise (SNR=25 dB); B) fully-sampled Cartesian k-space, where odd lines of Cartesian k-space are shifted by 1 pixel to simulate an imperfectly aligned EPI trajectory.

For each experiment, complex k-space data $$$x$$$ was provided to the input of a multilayer perceptron neural network, in which each layer is fully connected by an affine mapping followed by a nonlinearity $$$g(x)=s(Wx+b)$$$ where $$$W$$$ is a $$$d '\times d$$$ weight matrix, $$$b$$$ is an offset vector, and $$$s$$$ is the activation function $$$\tanh$$$. The fully-connected output layer is connected to a convolutional autoencoder [6] using a 6x6 kernel and 2x2 stride to generate 128 feature maps. The network parameters were trained to minimize squared loss and updated by ADAGRAD stochastic gradient descent [7], computed with Tensorflow [8] on two NVIDIA Tesla P100 GPUs.

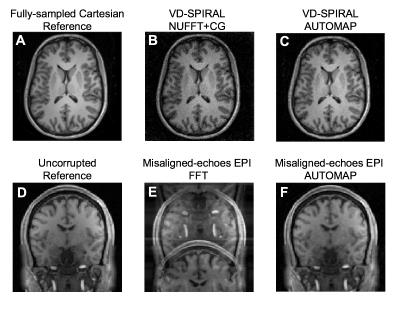
The trained model was validated with in-vivo data obtained from the Human Connectome Project [9] with T1-weighted 3D MPRAGE with TR=2530ms, TE=1.15ms, TI=1100ms, FA=7.0 deg, BW=651 Hz/Px). The k-space of representative slices were generated as described above and then processed through the feedforward network (reconstruction time approx. 1 second) to obtain reconstructions (Figure 2). For comparison, a conventional FFT reconstruction is shown for experiment B and a NUFFT with conjugate-gradient iteration [10] for experiment A.

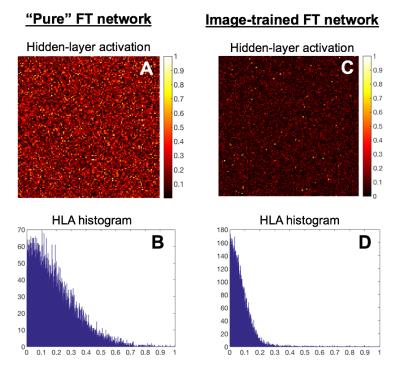
The sparsity of hidden layer activations is a common measure of neural network efficiency. Hidden layer activations of the network trained on images is substantially sparser than a “pure” Fourier transform network trained on random k-space inputs (Figure 3), indicating successful extraction of robust features [11] and is consistent with the noise immunity of AUTOMAP exhibited by our experiments.

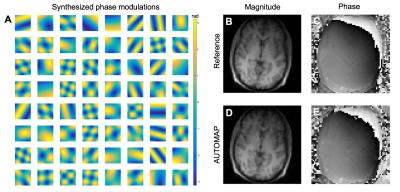
Training AUTOMAP on large image databases such as IMAGENET or PACS repositories is potentially problematic as image data are almost exclusively magnitude-only, which precludes AUTOMAP from learning how to properly reconstruct phase of complex k-space data. As a solution to this problem, modulation of our training data with smoothly-varying synthetic phase to the training dataset enables AUTOMAP to properly reconstruct both the magnitude and phase of k-space data (Figure 4).

We have shown an end-to-end automated k-space-to-image-space generalized reconstruction framework that demonstrates superior immunity to noise and acquisition artifacts. We anticipate AUTOMAP to be robust to a broad class of artifacts including motion, chemical shift, and signal chain imperfections such as gradient nonlinearity.

Acknowledgements

B.Z. was supported by National Institutes of Health / National Institute of Biomedical Imaging and Bioengineering F32 Fellowship (EB022390). The authors also acknowledge Dr. Mark Michalski and the resources of the MGH Clinical Data Science Center. Data were provided in part by the Human Connectome Project, MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga and Van Wedeen; U01MH093765) funded by the NIH Blueprint Initiative for Neuroscience Research grant; the National Institutes of Health grant P41EB015896; and the Instrumentation Grants S10RR023043, 1S10RR023401, 1S10RR019307.

References

[1] K. Hornik, M. Stinchcombe, and H. White, “Multilayer feedforward networks are universal approximators,” Neural Networks, vol. 2, no. 5, pp. 359–366, Jan. 1989.

[2] P. Vincent, H. Larochelle, I. Lajoie, Y. Bengio, and P.-A. Manzagol, “Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion,” Journal of Machine Learning Research, vol. 11, no. Dec, pp. 3371–3408, 2010.

[3] S. T. Roweis and L. K. Saul, “Nonlinear Dimensionality Reduction by Locally Linear Embedding,” Science, vol. 290, no. 5500, pp. 2323–2326, Dec. 2000.

[4] http://www.image-net.org

[5] Greengard, L., & Lee, J.-Y. (2006). Accelerating the Nonuniform Fast Fourier Transform. SIAM Review. http://doi.org/10.1137/S003614450343200X

[6] Masci, Jonathan, et al. "Stacked convolutional auto-encoders for hierarchical feature extraction." International Conference on Artificial Neural Networks. Springer Berlin Heidelberg, 2011.

[7] Duchi, John, Elad Hazan, and Yoram Singer. "Adaptive subgradient methods for online learning and stochastic optimization." Journal of Machine Learning Research 12.Jul (2011): 2121-2159.

[8] Abadi, Martin, et al. "Tensorflow: Large-scale machine learning on heterogeneous distributed systems." arXiv preprint arXiv:1603.04467 (2016).

[9] Marcus DS, Harwell J, Olsen T, Hodge M, Glasser MF, Prior F, Jenkinson M, Laumann T, Curtiss SW, Van Essen DC. Informatics and data mining tools and strategies for the human connectome project. Front Neuroinform 2011;5:4.

[10] Guerquin-Kern, Matthieu, et al. "A fast wavelet-based reconstruction method for magnetic resonance imaging." IEEE transactions on medical imaging 30.9 (2011): 1649-1660.

[11] Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., & Manzagol, P.-A. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. Journal of Machine Learning Research, 11(Dec), 3371–3408.

Figures

Figure 1: Neural network architecture of AUTOMAP reconstruction. An optimal mapping between k-space and image space is trained by nonlinear regression via fully-connected layers 1-3 by universal function approximation, and manifold learning with layers 1-3 projecting noisy reconstructed points toward the data manifold and layers 3-5 extracting local spatial correlation features by convolutional autoencoding. The system is agnostic towards k-space ordering, thus the same network architecture (changing only layer size, if needed) can be used to train any k-space trajectory including undersampled, non-Cartesian, and non-Fourier acquisitions. To demonstrate generalizability, all training data were derived from IMAGENET photographs of natural scenes.

Figure 2: Reconstruction performance. (A) Fully-sampled Cartesian reference data is regridded to a variable-density spiral trajectory with NUFFT and corrupted by additive Gaussian noise. Reconstructions by (B) NUFFT with Conjugate Gradient iteration and by (C) AUTOMAP are shown. (D) Fully-sampled Cartesian reference data is corrupted by odd-line k-space shift to simulate misaligned echoes experienced by imperfect EPI acquisition. (E) Conventional Fourier Transform exhibits N/2 ghosting, which is absent in the AUTOMAP reconstruction (F).

Figure 3: Sparsity of hidden-layer activations. A reconstruction trained exclusively on pairs of random k-space inputs and Fourier-Transformed outputs closely represents a “pure” Fourier Transform process. MR validation data processed through this network results in high-amplitude and widely-distributed hidden-layer activations (HLA), which are the output values of Layer 2 nodes (A). Histogram analysis of the activation values are shown in (B). In contrast, an image-trained AUTOMAP network results in far sparser hidden-layer activations (C,D) for the same validation data; thus the image-trained system captures the advantages of network sparsity such as noise-robustness and efficient feature extraction [11].

Figure 4: Learning phase reconstruction. The IMAGENET training data are magnitude-only, but the inclusion of synthetic phase to the training dataset enables AUTOMAP to properly reconstruct both the magnitude and phase of k-space data. The IMAGENET k-space training data was phase-modulated by 2-dimesional sinusoids of varying spatial frequencies (A). The magnitude (B) and phase (C) of the reference data are properly reconstructed by AUTOMAP trained in this manner (D, E).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0640