0607

Robust Estimation and In-vivo Validation of the Axon Bundle Diffusivity Profiles

Ricardo Coronado-Leija¹, Alonso Ramirez-Manzanares¹, and Jose Luis Marroquin¹

¹Computer Science, Centro de Investigacion en Matematicas, Guanajuato, Mexico

Synopsis

A stable, accurate and robust-to-noise general framework for the estimation of the intra-voxel axial and radial diffusivity parameters for diffusion-weighted magnetic resonance imaging is presented. The method estimates the diffusion profiles at multi-fiber voxels, improving the estimation of the intra-voxel geometry at challenging microstructure configurations. It naturally constrains the sparsity on the recovered solutions and exploits the spatial redundancy of the axon packs. A useful evaluation metric is proposed: it combines the information of the success rate of the number of bundles and their angular error. A new evaluation method for the in-vivo estimations on large datasets is also proposed.

Introduction and Purpose

The estimation of water molecular displacements from DW-MRI allows inferring the neuronal connections architecture. Spherical Deconvolution (CSD)¹ has become very popular because the reasonable number of acquisitions used to recover the fiber orientation distribution function. Some disadvantages are: a) it does not explicitly estimate voxel-wise diffusivity profiles but keeps them fixed. This constant deconvolution response-function assumption is not completely valid even on healthy white-matter (WM)², and could result in incorrect estimations of the number of diffusion compartments³, b) its inability to disentangle bundle populations on small crossing angles ($$$< 45^{\circ}$$$) and the uncertainty on the estimated orientations^4,5. It is important to tackle the drawbacks above in order to the improve estimation of bundle-wise microstructure parameters. Here, we propose a general adaptive framework of the response function at each voxel to estimate diffusion multi-compartment parameters from multi-shell data.

Methods

This work illustrates the estimation of the axial and radial diffusivity from a Gaussian Mixture Model (GMM), however our framework can be used for different tissue models. Given a robust estimation of the bundles number and orientations provided by the fixed-response-function MRDS⁶ we develop a framework to estimate the axial/radial diffusivities $$$\left\{\lambda_{k}^{\|},\lambda_{k}^{\bot}\right\}$$$. MRDS was set to recover a maximum of $$$N=3$$$ tensors per voxel to keep the optimization search space for the diffusivity profiles manageable. This optimization is iterated jointly with the MRDS stage, which re-computes the compartment sizes and orientations from an iteratively-updated response function. To compute the final number of bundles per voxel, the F-Test model-selection is used, which is the recommended selector for the nested models⁷ on the GMM formulation. The Simultaneous Denoising and Fitting strategy (SDF)⁶ is also applied; however, to avoid the blurring of local features, $$$\left\{\lambda_{k}^{\|},\lambda_{k}^{\bot}\right\}$$$ are computed only from individual voxel signals. We demonstrate the advantages of combining two widely used performance metrics^4,5: Success Rate (SR) and Angular Error ($$$\epsilon_{\theta}$$$), in a more informative metric $$$SR^{\theta}$$$ which quantifies the proportion in which an algorithm estimates the correct number of bundles and their orientations with an angular error $$$< \theta$$$.

Gold Standards for the validation on in-vivo data

The proper validation of estimations on in-vivo data is still a challenging open problem. Here we propose a methodology to create robust Gold Standards (GS) from the MASSIVE data set⁸. We created GSs by using the Bootstrap Aggregating Methodology which reduces the variance of the estimators and the effect of the outliers: it takes a large number of Bootstrap samples, fits a model (CSD, MRDS, etc.) on each sample, and averages the results over all the samples to create a robust estimator. The Bootstrap sampling is a natural option for GS construction on in-vivo data because they present strong outliers due to misalignments, eddy currents, etc. The quality of the GS is verified quantitatively first on synthetic data, then used to evaluate in-vivo results.

Experiments and Results

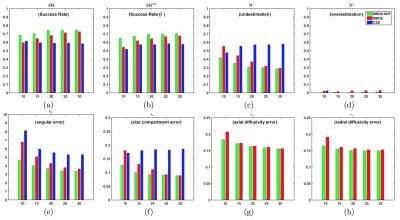
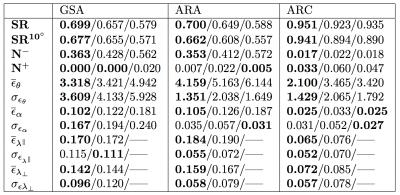
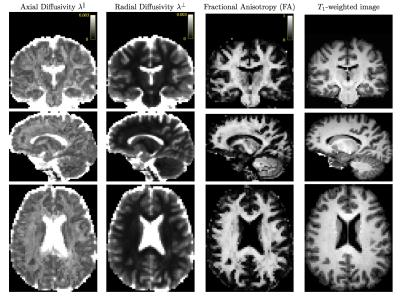
Realistic synthetic MR signals are generated from state-of-the-art multi-compartment models with intra/extra/isotropic compartments⁹. In all the experiments we use 64 DW signals for $$$b$$$-value = 3000 $$$s/mm^{2}$$$, 16 for $$$b$$$-value = 1000 $$$s/mm^{2}$$$, and 10 $$$S_{0}$$$. We compared against the recent multi-shell CSD¹⁰ MRtrix-3 implementation, $$$\ell$$$=8, and $$$th=$$$0.1¹⁰. The importance of the response function estimation is demonstrated in Figure 1. Results from synthetic experiments on the spatially-coherent phantom in⁵ are in Figure 2. To build the best as possible GS for in-vivo data, we first create and evaluate GSs for CSD, MRDS and MRDS-SDF for this synthetic phantom using 100 Bootstrap samples. To evaluate the GS-accuracy (GSA) for the three methods, their error with respect to the Ground Truth (GT) of the phantom is computed. We also computed the average realization accuracy (ARA: the errors of the parameters estimated with each method from each sample against the GT), and the average realization consistency (ARC: the errors of the parameters estimated with each method from each sample against their respective GS). The results about the GS’s quality above are presented in Table 1. Based on the evidence from extensive realistic synthetic experiments, we use the MRDS-SDF GS as the best pseudo-GT for in-vivo experiments. The performance of the methodologies w.r.t. this in-vivo pseudo GT is presented in Figure 3. Figure 4 shows slices for the single Bootstrap sample voxel-wise diffusivity profiles computed using MRDS-SDF. MRDS computational time is 9 times larger than CSD’s (voxel-wise).

Conclusions

An accurate and robust-to-noise algorithm and a framework for the validation on large in-vivo datasets is presented. It improves the existing approaches in the estimation of the number of axon bundles, their orientation and radial/axial diffusivities at challenging configurations: small crossing angles and different voxel-wise anisotropic diffusion profiles.

Acknowledgements

R. Coronado-Leija was supported by a Ph.D. scholarship from CONACYT, Mexico. A. Ramirez-Manzanares and J.L. Marroquin were partially supported by SNI-CONACYT, Mexico, (Grants 169338 and 6243).

References

1. Tournier J. D. , Yeh C. H., et al. Resolving crossing fibres using constrained spherical deconvolution: Validation using diffusion-weighted imaging phantom data. NeuroImage. 2008;42(2): 617-625.

2. Gulani V. and Webb A.G., et al. Apparent diffusion tensor measurements in myelin-deficient rat spinal cords. Mag. Reson. in Med. 2001;45(2): 191-195.

3. Parker G.D., Marshall D., et al. A pitfall in the reconstruction of fibre ODFs using spherical deconvolution of diffusion MRI data. NeuroImage. 2013; 65(1): 433-448.

4. Ramirez-Manzanares A., Cook, P. A., et al. Resolving axon fiber crossings at clinical b-values: An evaluation study. Medical Physics. 2011; 38(9): 5239-5253.

5. Daducci A., Canales-Rodríguez E.J., et al. Quantitative Comparison of Reconstruction Methods for Intra-Voxel Fiber Recovery From Diffusion MRI. IEEE Trans. on Med. Imag. 2014;33(2): 384-399.

6. Coronado-Leija R., Ramirez-Manzanares A., et al. Accurate Multi-resolution Discrete Search Method to Estimate the Number and Directions of Axon Packs from DWMRI . Proc. Intl. Soc. Mag. Reson. Med. 23. 2015:565.

7. Burnham K. Model selection and multimodel inference : a practical information-theoretic approach. Springer, New York. 2002.

8. Froeling M., Tax C.M.W., et al. MASSIVE Brain Dataset: Multiple Acquisitions for Standardization of Structural Imaging Validation and Evaluation. Mag. Reson. in Med. 2016; DOI:10.1002/mrm.26259.

9. Panagiotaki E., Schneider T., et al. Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison. NeuroImage. 2012; 59(3): 224-2254.

10. Jeurissen, B., Tournier J.D., et al. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage. 2014;103:411-426.

Figures

Figure 1. Importance of the response function estimation. $$$SR^{10^{\circ}}$$$ for MRDS with estimation of axial and radial diffusivities, MRDS-fixed-response-function, and CSD methods. TOP SNR = 15, BOTTOM SNR = 25. Even with a fixed response function, the performance of MRDS is better than that of CSD, but this difference significantly increases when the diffusion profile $$$\left\{ \lambda^{\|},\lambda^{\bot} \right\}$$$ is estimated. CSD and MRDS with fixed response function have good performances only when the diffusion profile in the signals and in the response function are similar, as reported in³. The performance is worse when the FA decreases.

Figure 2. Overall results (MRDS-SDF, MRDS and CSD) on the phantom in⁵ with synthetic multi-compartment signals, FA in [0.75,0.90]. Error metrics as in⁵. Voxel-wise MRDS shows better performance than CSD for all the SNR ($$$x$$$-axis) for most of the cases. MRDS-SDF improves the performance for low SNRs presenting better results than both CSD and MRDS. More importantly, the estimation of the eigenvalues of the multi-tensors was also better using MRDS-SDF. The improvements are achieved even when the eigenvalues are obtained using only the information of the signal in its own voxel without using spatial regularization on this estimation stage.

Table 1. GSA, ARA and ARC for the GSs on the challenging spatially coherent phantom used in⁵. Results are in the format MRDS-SDF/MRDS/CSD (best result per category in bold). Error metrics as in Figure 2, $$$\sigma$$$=std. MRDS-SDF performs best for almost all metrics, demonstrating the advantages of the integration of spatial information. Comparing MRDS against CSD, MRDS is better for GSA and ARA, i.e. MRDS is more accurate than CSD. For ARC, CSD is slightly more consistent on each sample than MRDS. MRDS and MRDS-SDF report accurate and consistent results on the estimation of the axial/radial diffusivities.

Figure 3. Comparison with the GS from the MASSIVE dataset. Reconstructions of the sagittal dODFs are shown for MRDS-SDF GS (the pseudo GT from Bootstrap) and for CSD, MRDS and MRDS-SDF single samples (80 DWIs). CSD shows zones in which fiber bundles appear discontinuous, while MRDS and MRDS-SDF capture those and additional fiber bundles. More importantly, the extra fiber bundles reported by MRDS and MRDS-SDF show good spatial coherence and are in correspondence with the GS, which indicates that these bundles are very likely to be present, showing a qualitatively smoother dODF field.

Figure 4. $$$\lambda^{\|}, \lambda^{\bot}$$$, FA and $$$T_{1}$$$ (left to right) maps for a single Boostrap sample (80 DWIs) from the MASSIVE dataset using the MRDS-SDF method. From top to bottom: coronal, sagittal and axial slices. Diffusivity units are in $$$mm^{2}/s$$$. The maps are smooth and the diffusivities $$$\lambda^{\|}, \lambda^{\bot}$$$ in the WM are inside the plausible ranges. A $$$T_{1}$$$ weighted image is also provided to demonstrate how the FA is high in the voxels that belong to the WM independently of the existence of crossing fiber bundles, and it is low when the voxel belongs to GM and CSF.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0607